»Урок 12. Рангът на матрицата. Изчисляване на ранга на матрицата. Матрична норма

Урок номер 12. Рангът на матрицата. Изчисляване на ранга на матрицата. Норма на матриците.

Ако всички малки на матрицатаАпоръчкакса равни на нула, то всички минорни от порядък k + 1, ако съществуват такива, също са равни на нула.
По ранга на матрицата А е най-големият от порядките на минорите на матрицата А различен от нула.
Максималният ранг може да бъде равен на минималния брой от броя на редовете или колоните на матрицата, т.е. ако матрицата е 4x5, тогава максималният ранг ще бъде 4.
Минималният ранг на матрица е 1, освен ако не се занимавате с нулева матрица, където рангът винаги е нула.

Рангът на недегенерирана квадратна матрица от порядък n е равен на n, тъй като нейната детерминанта е минор от порядък n и неизродената матрица е ненула.
Когато матрицата се транспонира, нейният ранг не се променя.

Нека рангът на матрицата е. Тогава се извиква всеки ненулев порядък основен минор.
Пример.Дадена матрица A.

Детерминантата на матрицата е нула.
Минор от втори ред ... Следователно r (A) = 2 и основният минор.
Основният минор също е минорът .
Незначителен от = 0, така че няма да е основно.
Упражнение: самостоятелно проверете кои други непълнолетни от втори ред ще бъдат основни и кои не.

Намирането на ранга на матрица чрез изчисляване на всички нейни минорни изисква твърде много изчислителна работа. (Читателят може да провери, че има 36 второстепенни минорни числа в квадратна матрица от четвърти ред.) Следователно се използва различен алгоритъм за намиране на ранга. Необходима е редица допълнителна информация, за да се опише.

Нека наречем следните действия върху матрици елементарни трансформации на матрици:
1) пермутация на редове или колони;
2) умножаване на ред или колона по число, различно от нула;
3) добавяне към един от редовете на друг ред, умножен по число, или добавяне към една от колоните на друга колона, умножен по число.

Елементарните трансформации не променят ранга на матрицата.
Алгоритъм за изчисляване на ранга на матрицае подобен на алгоритъма за изчисляване на детерминанта и се състои във факта, че с помощта на елементарни трансформации матрицата се свежда до проста форма, за която не е трудно да се намери ранг. Тъй като рангът не се променя с всяка трансформация, тогава чрез изчисляване на ранга на трансформираната матрица, по този начин намираме ранга на оригиналната матрица.

Нека се изисква да се изчисли ранга на матрицата на размера мхн.

В резултат на изчисленията матрицата A1 има формата

Ако всички линии, започващи от третия, са нула, тогава от непълнолетни ... В противен случай, чрез пренареждане на редове и колони с числа по-големи от две, постигаме третият елемент от третия ред да е различен от нула. Освен това, като добавим третия ред, умножен по съответните числа, към редовете с големи числа, получаваме нули в третата колона, започвайки от четвъртия елемент и т.н.
На някакъв етап стигаме до матрица, в която всички редове, започвайки от (r + 1) th, са равни на нула (или липсват за), а минорът в първите редове и първите колони е детерминантата на a триъгълна матрица с ненулеви елементи по диагонала ... Рангът на такава матрица е. Следователно Rang (A) = r.

В предложения алгоритъм за намиране на ранга на матрица всички изчисления трябва да се извършват без закръгляване. Произволно малка промяна в поне един от елементите на междинните матрици може да доведе до факта, че полученият отговор ще се различава от ранга на оригиналната матрица с няколко единици.
Ако елементите в оригиналната матрица са цели числа, тогава е удобно да се извършват изчисления, без да се използват дроби. Следователно на всеки етап е препоръчително низовете да се умножават по числа, така че дробите да не се появяват в изчисленията.

В практическата лабораторна работа разгледайте пример за намиране на ранга на матрица.

АЛГОРИТЪМ ЗА МЕСТОПОЛОЖЕНИЕ МАТРИЧНИ СТАНДАРТИ .
Има само три матрични норми.
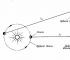
Първата норма на матрицата= максимумът от числата, получени чрез събиране на всички елементи на всяка колона, взети по модул.
Пример: нека е дадена матрица 3x2 A (фиг. 10). Първата колона съдържа елементи: 8, 3, 8. Всички елементи са положителни. Нека намерим тяхната сума: 8 + 3 + 8 = 19. Втората колона съдържа елементи: 8, -2, -8. Два елемента са отрицателни, следователно, когато се добавят тези числа, е необходимо да се замени модулът на тези числа (тоест без знаците "минус"). Нека намерим тяхната сума: 8 + 2 + 8 = 18. Максимумът на тези две числа е 19. Така че първата норма на матрицата е 19.

Фигура 10.

Втора норма на матрицатае корен квадратен от сбора от квадратите на всички елементи на матрицата. И това означава, че квадратуваме всички елементи на матрицата, след това добавяме получените стойности и извличаме квадратния корен от резултата.
В нашия случай 2 норма на матрицата е равна на квадратен корен от 269. На диаграмата грубо извадих квадратния корен от 269 и в резултат получих около 16,401. Въпреки че е по-правилно да не се извлича коренът.

Трета норма на матрицатае максимумът от числата, получени чрез събиране на всички елементи от всеки ред, взети по модул.
В нашия пример: първият ред съдържа елементи: 8, 8. Всички елементи са положителни. Нека намерим тяхната сума: 8 + 8 = 16. Вторият ред съдържа елементи: 3, -2. Един от елементите е отрицателен, следователно, когато добавяте тези числа, трябва да замените модула на това число. Нека намерим тяхната сума: 3 + 2 = 5. Третият ред съдържа елементи 8 и -8. Един от елементите е отрицателен, следователно, когато добавяте тези числа, трябва да замените модула на това число. Нека намерим тяхната сума: 8 + 8 = 16. Максимумът на тези три числа е 16. Така че третата норма на матрицата е 16.

Съставител: Saliy N.A.

Колегиален YouTube

1 / 1

✪ Векторна норма. част 4.

Субтитри

Определение

Нека K е основното поле (обикновено К = Р или К = ° С ) и е линейното пространство на всички матрици с m реда и n колони, състоящи се от елементи K. В пространството на матриците се дава норма, ако всяка матрица е свързана с неотрицателно реално число ‖ A ‖ (\ displaystyle \ | A \ |), наречена своя норма, така че

В случай на квадратни матрици (т.е. м = н), матриците могат да се умножават без да напускат пространството и следователно нормите в тези пространства обикновено също удовлетворяват свойството субмултипликативност :

Субмултипликативността може да се извърши и за нормите на неквадратни матрици, но дефинирани за няколко необходими размера наведнъж. А именно, ако A е матрица ℓ  ×  м, а B е матрицата м ×  н, тогава А Б- матрица ℓ  ×  н .

Операторски норми

Важен клас матрични норми са операторски норми, наричан още подчинени или индуцирана ... Операторната норма е уникално конструирана според две норми, дефинирани в и, изхождайки от факта, че всяка матрица м ×  нсе представя с линеен оператор от K n (\ displaystyle K ^ (n)) v K m (\ displaystyle K ^ (m))... по-конкретно,

‖ A ‖ = sup (‖ A x ‖: x ∈ K n, ‖ x ‖ = 1) = sup (‖ A x ‖ ‖ x ‖: x ∈ K n, x ≠ 0). (\ displaystyle (\ начало (подравнено) \ | A \ | & = \ sup \ (\ | Ax \ |: x \ в K ^ (n), \ \ | x \ | = 1 \) \\ & = \ sup \ left \ ((\ frac (\ | Ax \ |) (\ | x \ |)): x \ in K ^ (n), \ x \ neq 0 \ right \). \ end (подравнен)))

При условие за последователно уточняване на нормите върху векторни пространства, такава норма е субмултипликативна (виж).

Примери за операторски норми

Свойства на спектралната норма:

1. Спектралната норма на оператор е равна на максималното единично число на този оператор.
2. Спектралната норма на нормален оператор е равна на абсолютната стойност на максималната собствена стойност по модул на този оператор.
3. Спектралната норма не се променя, когато матрицата се умножи по ортогонална (унитарна) матрица.

Неоператорски матрични норми

Има матрични норми, които не са операторни норми. Концепцията за неоператорни норми на матрици е въведена от Ю. И. Любич и е изследвана от G.R.Belitskii.

Пример за неоператорна норма

Например, разгледайте две различни операторски норми ‖ A ‖ 1 (\ displaystyle \ | A \ | _ (1))и ‖ A ‖ 2 (\ displaystyle \ | A \ | _ (2)), като норми на редове и колони. Формиране на нова норма ‖ A ‖ = m a x (‖ A ‖ 1, ‖ A ‖ 2) (\ displaystyle \ | A \ | = max (\ | A \ | _ (1), \ | A \ | _ (2)))... Новата норма има свойството пръстен ‖ A B ‖ ≤ ‖ A ‖ ‖ B ‖ (\ displaystyle \ | AB \ | \ leq \ | A \ | \ | B \ |), запазва единството ‖ I ‖ = 1 (\ displaystyle \ | I \ | = 1)и не е оператор.

Примери за норми

вектор p (\ displaystyle p)-норма

Може да се разглежда m × n (\ displaystyle m \ times n)матрица като вектор на размера m n (\ displaystyle mn)и използвайте стандартни векторни норми:

‖ A ‖ p = ‖ vec (A) ‖ p = (∑ i = 1 m ∑ j = 1 n | aij | p) 1 / p (\ displaystyle \ | A \ | _ (p) = \ | \ mathrm ( vec) (A) \ | _ (p) = \ left (\ sum _ (i = 1) ^ (m) \ sum _ (j = 1) ^ (n) | a_ (ij) | ^ (p) \ вдясно) ^ (1 / p))

Нормата на Фробениус

Нормата на Фробениус, или Евклидова нормае частен случай на p-нормата за стр = 2 : ‖ A ‖ F = ∑ i = 1 m ∑ j = 1 naij 2 (\ displaystyle \ | A \ | _ (F) = (\ sqrt (\ sum _ (i = 1) ^ (m) \ sum _ (j) = 1) ^ (n) a_ (ij) ^ (2)))).

Нормата на Фробениус е лесна за изчисляване (в сравнение, например, със спектралната норма). Притежава следните свойства:

‖ A x ‖ 2 2 = ∑ i = 1 m | ∑ j = 1 n a i j x j | 2 ≤ ∑ i = 1 m (∑ j = 1 n | a i j | 2 ∑ j = 1 n | x j | 2) = ∑ j = 1 n | x j | 2 ‖ A ‖ F 2 = ‖ A ‖ F 2 ‖ x ‖ 2 2. (\ displaystyle \ | Ax \ | _ (2) ^ (2) = \ sum _ (i = 1) ^ (m) \ left | \ sum _ (j = 1) ^ (n) a_ (ij) x_ ( j) \ вдясно | ^ (2) \ leq \ sum _ (i = 1) ^ (m) \ вляво (\ sum _ (j = 1) ^ (n) | a_ (ij) | ^ (2) \ sum _ (j = 1) ^ (n) | x_ (j) | ^ (2) \ вдясно) = \ сума _ (j = 1) ^ (n) | x_ (j) | ^ (2) \ | A \ | _ (F) ^ (2) = \ | A \ | _ (F) ^ (2) \ | x \ | _ (2) ^ (2).)

• Субмножественост: ‖ A B ‖ F ≤ ‖ A ‖ F ‖ B ‖ F (\ displaystyle \ | AB \ | _ (F) \ leq \ | A \ | _ (F) \ | B \ | _ (F)), защото ‖ A B ‖ F 2 = ∑ i, j | ∑ k a i k b k j | 2 ≤ ∑ i, j (∑ k | a i k | | b k j |) 2 ≤ ∑ i, j (∑ k | a i k | 2 ∑ k | b k j | 2) = ∑ i, k | a i k | 2 ∑ k, j | b k j | 2 = ‖ A ‖ F 2 ‖ B ‖ F 2 (\ displaystyle \ | AB \ | _ (F) ^ (2) = \ sum _ (i, j) \ left | \ sum _ (k) a_ (ik) b_ (kj) \ надясно | ^ (2) \ leq \ sum _ (i, j) \ left (\ sum _ (k) | a_ (ik) || b_ (kj) | \ вдясно) ^ (2) \ leq \ sum _ (i, j) \ left (\ sum _ (k) | a_ (ik) | ^ (2) \ sum _ (k) | b_ (kj) | ^ (2) \ right) = \ sum _ (i, k) | a_ (ik) | ^ (2) \ сума _ (k, j) | b_ (kj) | ^ (2) = \ | A \ | _ (F) ^ (2) \ | B \ | _ (F) ^ (2)).
• ‖ A ‖ F 2 = tr ⁡ A ∗ A = tr ⁡ AA ∗ (\ displaystyle \ | A \ | _ (F) ^ (2) = \ mathop (\ rm (tr)) A ^ (*) A = \ mathop (\ rm (tr)) AA ^ (*)), където t r ⁡ A (\ displaystyle \ mathop (\ rm (tr)) A)- матрична следа A (\ displaystyle A), A ∗ (\ displaystyle A ^ (*))е ермитова конюгирана матрица.
• ‖ A ‖ F 2 = ρ 1 2 + ρ 2 2 + ⋯ + ρ n 2 (\ displaystyle \ | A \ | _ (F) ^ (2) = \ rho _ (1) ^ (2) + \ rho _ (2) ^ (2) + \ точки + \ rho _ (n) ^ (2)), където ρ 1, ρ 2,…, ρ n (\ displaystyle \ rho _ (1), \ rho _ (2), \ dots, \ rho _ (n))- единични стойности на матрицата A (\ displaystyle A).
• ‖ A ‖ F (\ displaystyle \ | A \ | _ (F))не се променя при умножение на матрица A (\ displaystyle A)ляво или дясно в ортогонални (унитарни) матрици.

Модул максимум

Максималната норма на модула е друг специален случай на p-нормата за стр = ∞ .

‖ A ‖ max = max (| a i j |). (\ displaystyle \ | A \ | _ (\ текст (макс.)) = \ max \ (| a_ (ij) | \).)

Нормата на Шатен

Консистенция на матричните и векторните норми

Матрична норма ‖ ⋅ ‖ a b (\ displaystyle \ | \ cdot \ | _ (ab))На K m × n (\ displaystyle K ^ (m \ пъти n))Наречен се съгласис норми ‖ ⋅ ‖ a (\ displaystyle \ | \ cdot \ | _ (a))На K n (\ displaystyle K ^ (n))и ‖ ⋅ ‖ b (\ displaystyle \ | \ cdot \ | _ (b))На K m (\ displaystyle K ^ (m)), ако:

‖ A x ‖ b ≤ ‖ A ‖ a b ‖ x ‖ a (\ displaystyle \ | Ax \ | _ (b) \ leq \ | A \ | _ (ab) \ | x \ | _ (a))

за всякакви A ∈ K m × n, x ∈ K n (\ displaystyle A \ in K ^ (m \ пъти n), x \ in K ^ (n))... Операторната норма по конструкция е съвместима с оригиналната векторна норма.

Примери за договорени, но не подчинени, матрични норми:

Еквивалентност на нормите

Всички норми в космоса K m × n (\ displaystyle K ^ (m \ пъти n))са еквивалентни, тоест за всякакви две норми ‖. ‖ Α (\ displaystyle \ |. \ | _ (\ Alpha))и ‖. ‖ Β (\ displaystyle \ |. \ | _ (\ Beta))и за всяка матрица A ∈ K m × n (\ displaystyle A \ in K ^ (m \ пъти n))двойното неравенство е вярно.

Матрична нормаще извикаме реалното число, присвоено на тази матрица || A || такова, което като реално число е свързано с всяка матрица от n-мерното пространство и удовлетворява 4 аксиоми:

1. || A || ³0 и || A || = 0 само ако A е нулева матрица;

2. || αA || = | α | · || A ||, където a R;

3. || A + B || £ || A || + || B ||;

4. || A · ​​B || £ || A || · || B ||. (мултипликативно свойство)

Нормата на матриците може да се въведе по различни начини. Матрица А може да се разглежда като n 2 -размерен вектор.

Тази норма се нарича евклидова норма на матрицата.

Ако за всяка квадратна матрица A и всеки вектор x, чиято размерност е равна на реда на матрицата, неравенството || Ax || £ || A || · || x ||

тогава се казва, че нормата на матрицата A е съвместима с нормата на вектора. Обърнете внимание, че отляво на последното условие е нормата на вектора (Ax е вектор).

С дадената векторна норма се координират различни матрични норми. Нека изберем най-малкия от тях. Това ще бъде

Тази матрична норма е подчинена на дадена векторна норма. Наличието на максимум в този израз следва от непрекъснатостта на нормата, тъй като винаги съществува вектор x -> || x || = 1 и || Ax || = || A ||.

Нека покажем, че нормата N (A) не подлежи на никаква векторна норма. Нормите на матрицата, подчинени на въведените по-рано векторни норми, се изразяват по следния начин:

1. || A || ¥ = | a ij | (норма-максимум)

2. || A || 1 = | a ij | (нормална сума)

3. || A || 2 =, (спектрална норма)

където s 1 е най-голямата правилна стойност на симетричната матрица A ¢ A, която е произведението на транспонираната и оригиналната матрици. T k матрицата A ¢ A е симетрична, тогава всички нейни собствени стойности са реални и положителни. Броят на l -свойствата е стойността, а ненулевият вектор x е собственият вектор на матрицата A (ако са свързани с релацията Ax = lx). Ако самата матрица A е симетрична, A ¢ = A, тогава A ¢ A = A 2 и след това s 1 =, където е най-голямата по модул собствена стойност на матрицата A. Следователно, в този случай имаме =.

Собствените стойности на матрицата не надвишават нито една от нейните договорени норми. Нормализиране на релацията, дефинираща собствените стойности, получаваме || λx || = || Ax ||, | λ | · || x || = || Ax || £ || A || · || x ||, | λ | £ || A ||

Тъй като е вярно || A || 2 £ || A || д, където евклидовата норма е лесна за изчисляване, в оценките вместо спектралната норма може да се използва евклидовата норма на матрицата.

30. Условност на системите от уравнения. Коефициент на условност .

Условност- влиянието на решението върху изходните данни. Ax = b: вектор бсъвпадащо решение х... Нека бъде бще се промени със сумата. След това векторът b +новото решение ще съвпада х + : A (x + ) = b +... Тъй като системата е линейна, тогава Брадва + А = b +, тогава А = ; = ; = ; b = Ax; = тогава; *, където е относителната грешка на смущението на решението, - фактор на състояниетоконд (A) (колко пъти може да се увеличи грешката на решението), е относителното смущение на вектора б. конд (A) = ; конд (A) *Свойства на коефициента: зависи от избора на матричната норма; конд ( = конд (A); умножаването на матрица по число не влияе на фактора на условието. Колкото по-голям е коефициентът, толкова повече грешката в изходните данни влияе върху решението на SLAE. Номерът на условието не може да бъде по-малък от 1.

31. Методът на размах за решаване на системи от линейни алгебрични уравнения.

Често е необходимо да се решават системи, чиито матрици, като са слабо запълнени, т.е. съдържащ много ненулеви елементи. Матриците на такива системи обикновено имат определена структура, сред която има системи с матрици с лентова структура, т.е. в тях ненулеви елементи са разположени на главния диагонал и на няколко странични диагонала. За решаване на системи с лентови матрици методът на Гаус може да бъде трансформиран в по-ефективни методи. Нека разгледаме най-простия случай на лентови системи, към който, както ще видим по-късно, решаването на задачи за дискретизация на гранични задачи за диференциални уравнения по методите на крайните разлики, крайните елементи и т.н., съседни на него:

Три диагонални матрици имат само (3n-2) ненулеви записи.

Нека преименуваме коефициентите на матрицата:

Тогава, в нотацията на компонентите, системата може да бъде представена като:

A i * x i-1 + b i * x i + c i * x i + 1 = d i , i = 1, 2, ..., n; (7)

a 1 = 0, c n = 0. (осем)

Структурата на системата предполага връзка само между съседни неизвестни:

x i = x i * x i +1 + h i (9)

x i -1 = x i -1 * x i + h i -1 и заместваме в (7):

A i (x i-1 * x i + h i-1) + b i * x i + c i * x i + 1 = d i

(a i * x i-1 + b i) x i = –c i * x i + 1 + d i –a i * h i-1

Сравнявайки получения израз с представянето (7), получаваме:

Формулите (10) представляват рекурентни отношения за изчисляване на коефициентите на размах. Те изискват задаване на първоначални стойности. В съответствие с първото условие (8) за i = 1 имаме a 1 = 0 и следователно

Освен това останалите коефициенти на размах се изчисляват и съхраняват по формули (10) за i = 2,3, ..., n, а за i = n, като се вземе предвид второто условие (8), получаваме xn = 0 . Следователно, в съответствие с формула (9) x n = h n.

След това, съгласно формулата (9), неизвестните x n -1, x n -2, ..., x 1 се намират последователно. Тази стъпка от изчислението се нарича обратен ход, докато изчисляването на коефициентите на размах се нарича премах.

За успешното прилагане на метода на почистване е необходимо в процеса на изчисления да няма ситуации с деление на нула, а при голям размер на системите не трябва да има бързо увеличаване на грешките при закръгляване. Ще извикаме бягането правилноако знаменателят на коефициентите на извъртане (10) не е в нула, и устойчивиако ½x i ½<1 при всех i=1,2,…, n. Достаточные условия корректности и устойчивости прогонки, которые во многих приложениях выполняются, определяются теоремой.

Теорема. Нека коефициентите a i и c i от уравнение (7) за i = 2,3, ..., n-1 се различават от нула и нека

½b i ½> ½a i ½ + ½c i ½ за i = 1, 2, ..., n. (единадесет)

Тогава размахът, определен от формули (10), (9), е правилен и стабилен.