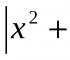Variabilní přírůstek. Otevřená knihovna - otevřená knihovna vzdělávacích informací

v lékařské a biologické fyzice

PŘEDNÁŠKA č. 1

DERIVATIVNÍ A DIFERENCIÁLNÍ FUNKCE.

SOUKROMÉ DERIVÁTY.

1. Pojem derivace, její mechanický a geometrický význam.

ale ) Argumenty a přírůstky funkcí.

Nechť je dána funkce y = f (x), kde x je hodnota argumentu z domény funkce. Vybereme-li z určitého intervalu domény funkce dvě hodnoty argumentu xo a x, pak se rozdíl mezi dvěma hodnotami argumentu nazývá přírůstek argumentu: x - xo = ∆x .

Hodnotu argumentu x lze určit pomocí x 0 a jeho přírůstku: x = x o + ∆x.

Rozdíl mezi dvěma hodnotami funkce se nazývá přírůstek funkce: ∆y = ∆f = f (x o + ∆x) - f (x o).

Přírůstek argumentu a funkce lze znázornit graficky (obr. 1). Přírůstky argumentů a přírůstky funkcí mohou být pozitivní nebo negativní. Jak vyplývá z obr. 1, geometricky je přírůstek argumentu ∆х znázorněn přírůstkem úsečky a přírůstek funkce ∆у je vyjádřen přírůstkem souřadnice. Výpočet přírůstku funkce by měl být proveden v následujícím pořadí:

dát argumentu přírůstek ∆x a získat hodnotu - x + ∆x;

2) najdeme hodnotu funkce pro hodnotu argumentu (x + ∆x) - f (x + ∆x);

3) najdeme přírůstek funkce ∆f = f (x + ∆x) - f (x).

Příklad: Určete přírůstek funkce y = x 2, pokud se argument změnil z x o = 1 na x = 3. Pro bod x o je hodnota funkce f (x o) = x² o; pro bod (x о + ∆х) hodnota funkce f (x о + ∆х) = (x о + ∆х) 2 = x² о + 2х о ∆х + ∆х 2, odkud ∆f = f (x о + ∆х) –f (х о) = (х о + ∆х) 2 –х² о = х² о + 2х о ∆х + ∆х 2 –х² о = 2х о ∆х + ∆х 2; ∆f = 2х о ∆х + ∆х 2; ∆х = 3–1 = 2; ∆f = 2 1 2 + 4 = 8.

b)Úkoly vedoucí k pojetí derivace. Definice derivátu, jeho fyzický význam.

Pojem přírůstku argumentu a funkce je nezbytný k zavedení pojmu derivace, který historicky vznikl na základě potřeby určit rychlost určitých procesů.

Zvažte, jak můžete určit rychlost přímočarého pohybu. Nechte tělo pohybovat se přímo podle zákona: ∆Ѕ =  · ∆t. Pro rovnoměrný pohyb:  = ∆Ѕ / ∆t.

U proměnného pohybu určuje hodnota ∆Ѕ / ∆t hodnotu av. , tj. srov. = ∆Ѕ / .t. Ale průměrná rychlost neumožňuje odrážet rysy pohybu těla a poskytnout představu o skutečné rychlosti v čase t. S poklesem časového intervalu, tj. při →t → 0 má průměrná rychlost sklon ke svému limitu - okamžitá rychlost:

 okamžité =
 st =
∆Ѕ / ∆t.

Okamžitá rychlost chemické reakce se určuje stejným způsobem:

 okamžité =
 st =
∆х / ∆t,

kde x je množství látky vytvořené během chemické reakce v čase t. Podobné úkoly pro stanovení rychlosti různých procesů vedly k zavedení konceptu derivace funkce v matematice.

Nechť je dána spojitá funkce f (x), definovaná na intervalu] a, v [a její přírůstek ∆f = f (x + ∆x) –f (x).
je funkcí ∆x a vyjadřuje průměrnou rychlost změny funkce.

Poměrový limit , když ∆х → 0, za předpokladu, že tento limit existuje, se nazývá derivace funkce :

y "x =

.

Derivát je označen:
- (prime x zdvih); f " (x) - (eff zdvih x) ; y "- (pomlčka); dy / dх – (de igrek po de iks); - (hra s tečkou).

Na základě definice derivace můžeme říci, že okamžitá rychlost přímočarého pohybu je časovou derivací dráhy:

 okamžité = S "t = f " (t).

Můžeme tedy dojít k závěru, že derivací funkce vzhledem k argumentu x je okamžitá rychlost změny funkce f (x):

y "x = f " (x) =  okamžitý.

Toto je fyzický význam derivace. Proces hledání derivace se nazývá diferenciace, takže výraz „diferencovat funkci“ je ekvivalentní výrazu „najít derivaci funkce“.

v)Geometrický význam derivace.

P
derivace funkce y = f (x) má jednoduchý geometrický význam spojený s konceptem tečny ke křivce v určitém bodě M. V tomto případě tečna, tj. přímka je analyticky vyjádřena jako y = kx = tanx, kde, – úhel sklonu tečny (přímky) k ose X. Představme spojitou křivku jako funkci y = f (x), vezmeme na křivce bod M a blízko něj bod M 1 a dát skrz ně skrz. Jeho sklon k sec = tan β = Pokud je bod М 1 přiblížen k M, pak přírůstek argumentu ∆х bude mít tendenci k nule a sečen v β = α zaujme polohu tečny. Z obr. 2 vyplývá: tgα =
tgβ =
= y "x. Ale tgα se rovná sklonu tečny k grafu funkce:

k = tgα =
= y "x = f " (X). Sklon tečny ke grafu funkce v daném bodě se tedy rovná hodnotě její derivace v bodě tečnosti. Toto je geometrický význam derivace.

d)Obecné pravidlo pro nalezení derivátu.

Na základě definice derivátu lze proces diferenciace funkce reprezentovat takto:

f (x + ∆x) = f (x) + ∆f;

najděte přírůstek funkce: ∆f = f (x + ∆x) - f (x);

tvoří poměr přírůstku funkce k přírůstku argumentu:

;

Příklad: f (x) = x 2; F " (x) =?.

Jak je však patrné iz tohoto jednoduchého příkladu, použití zadané sekvence při přijímání derivátů je pracný a složitý proces. Proto pro různé funkce obecné vzorce diferenciace, které jsou prezentovány ve formě tabulky „Základní vzorce pro diferenciaci funkcí.“

V životě nás nezajímají vždy přesné hodnoty jakýchkoli veličin. Někdy je zajímavé znát změnu této hodnoty, například průměrnou rychlost sběrnice, poměr množství pohybu k časovému intervalu atd. Chcete-li porovnat hodnotu funkce v určitém okamžiku s hodnotami stejné funkce v jiných bodech, je vhodné použít pojmy jako „přírůstek funkce“ a „přírůstek argumentu“.

Pojmy „přírůstek funkce“ a „přírůstek argumentu“

Předpokládejme, že x je libovolný bod, který leží v nějakém sousedství bodu x0. Přírůstkem argumentu v bodě x0 je rozdíl x-x0. Přírůstek je indikován následovně: ∆х.

• ∆x = x-x0.

Někdy se tato hodnota nazývá přírůstek nezávislé proměnné v bodě x0. Z vzorce vyplývá: x = x0 + ∆x. V takových případech se říká, že počáteční hodnota nezávislé proměnné x0 přijala přírůstek ∆x.

Změníme-li argument, změní se také hodnota funkce.

• f (x) - f (x0) = f (x0 + ∆х) - f (x0).

Přírůstek funkce f v bodě x0, rozdíl f (x0 + ∆x) - f (x0) se nazývá odpovídající přírůstku ∆x. Přírůstek funkce je označen jako ∆f. Podle definice tedy získáme:

• ∆f = f (x0 + ∆x) - f (x0).

Někdy se ∆f nazývá také přírůstek závislé proměnné a ∆y se používá k jeho označení, pokud byla funkce například y = f (x).

Geometrický význam přírůstku

Podívejte se na následující obrázek.

Jak vidíte, přírůstek ukazuje změnu v souřadnici a úsečce bodu. A poměr přírůstku funkce k přírůstku argumentu určuje úhel sklonu sekundy procházející počáteční a konečnou polohou bodu.

Zvažte příklady přírůstků funkcí a argumentů

Příklad 1. Najděte přírůstek argumentu ∆x a přírůstek funkce ∆f v bodě x0, pokud f (x) = x 2, x0 = 2 a) x = 1,9 b) x = 2,1

Použijme výše uvedené vzorce:

a) ∆х = х-х0 = 1,9 - 2 = -0,1;

• ∆f = f (1,9) - f (2) = 1,9 2 - 2 2 = -0,39;

b) ∆x = x-x0 = 2,1-2 = 0,1;

• ∆f = f (2.1) - f (2) = 2,1 2 - 2 2 = 0,41.

Příklad 2. Vypočítejte přírůstek ∆f pro funkci f (x) = 1 / x v bodě x0, pokud je přírůstek argumentu roven ∆x.

Opět použijeme vzorce získané výše.

• ∆f = f (x0 + ∆x) - f (x0) = 1 / (x0-∆x) - 1 / x0 = (x0 - (x0 + ∆x)) / (x0 * (x0 + ∆x)) = - ∆x / ((x0 * (x0 + ∆x)).

Nechť x je libovolná bodová poleva v nějakém sousedství pevného bodu x 0. rozdíl x - x 0 se obvykle nazývá přírůstek nezávislé proměnné (nebo přírůstek argumentu) v bodě x 0 a označuje se Δx. Takto,

Δx = x –x 0,

odkud to vyplývá

Přírůstek funkce - rozdíl mezi dvěma hodnotami funkce.

Nechte funkci na = f (x), definováno, když je hodnota argumentu rovna X 0. Dejte argumentu přírůstek D X, ᴛ.ᴇ. považujte hodnotu argumentu za stejnou X 0 + D X... Předpokládejme, že tato hodnota argumentu je také v rozsahu této funkce. Pak rozdíl D y = f (x 0 + D X) – f (x 0) je zvykem volat přírůstek funkce. Přírůstek funkce F(X) na místě X je funkce obvykle označená Δ x f z nové proměnné Δ X definováno jako

Δ x f(Δ X) = F(X + Δ X) − F(X).

Najděte přírůstek argumentu a přírůstek funkce v bodě x 0, pokud

Příklad 2. Najděte přírůstek funkce f (x) = x 2, pokud x = 1, ∆x = 0,1

Řešení: f (x) = x 2, f (x + ∆x) = (x + ∆x) 2

Najděte přírůstek funkce ∆f = f (x + ∆x) - f (x) = (x + ∆x) 2 - x 2 = x 2 + 2x * ∆x + ∆x 2 - x 2 = 2x * ∆x + ∆x 2 /

Dosazením hodnot x = 1 a ∆x = 0,1 získáme ∆f = 2 * 1 * 0,1 + (0,1) 2 = 0,2 + 0,01 = 0,21

Najděte přírůstek argumentu a přírůstek funkce v bodě x 0

2.f (x) = 2x 3.x 0 = 3 x = 2.4

3.f (x) = 2x 2 +2 x 0 = 1 x = 0,8

4.f (x) = 3x + 4 x 0 = 4 x = 3,8

Definice: Derivát funkce v bodě, je obvyklé volat limit (pokud existuje a je konečný) poměru přírůstku funkce k přírůstku argumentu, za předpokladu, že tato má sklon k nule.

Nejčastěji se používají následující označení derivátů:

Takto,

Hledání derivátu se obvykle nazývá diferenciace ... Představený definice rozlišitelné funkce: Funkce f, která má derivaci v každém bodě určitého intervalu, se obvykle nazývá diferencovatelná v daném intervalu.

Nechť je funkce definována v nějakém sousedství bodu Derivace funkce se obvykle nazývá číslo tak, že funkce v sousedství U(X 0) lze reprezentovat jako

F(X 0 + h) = F(X 0) + Ah + Ó(h)

pokud existuje.

Určení derivace funkce v bodě.

Nechte funkci f (x) definované v intervalu (a; b), a jsou body tohoto intervalu.

Definice... Derivační funkce f (x) v bodě je zvykem volat limit poměru přírůstku funkce k přírůstku argumentu v. Je to uvedeno.

Když poslední limit získá určitou konečnou hodnotu, pak mluví o existenci konečná derivace v bodě... Pokud je limit nekonečný, pak to říkají derivace je v daném bodě nekonečná... Pokud limit neexistuje, pak derivace funkce v tomto okamžiku neexistuje.

Funkce f (x) se nazývá diferencovatelný v bodě, kdy má konečnou derivaci.

Pokud je funkce f (x) diferencovatelné v každém bodě nějakého intervalu (a; b), pak se funkce v tomto intervalu nazývá diferencovatelná. Any ᴏϬᴩᴀᴈᴏᴍ, jakýkoli bod X z toho mezi (a; b) můžeme v tomto okamžiku přiřadit hodnotu derivace funkce, to znamená, že máme příležitost definovat novou funkci, která se nazývá derivace funkce f (x) na intervalu (a; b).

Hledání derivace se obvykle nazývá diferenciace.

Definice 1

Pokud je pro každý pár $ (x, y) $ hodnot dvou nezávislých proměnných z určité oblasti přidružena určitá hodnota $ z $, pak se říká, že $ z $ je funkcí dvou proměnných $ (x, y) $. Zápis: $ z = f (x, y) $.

Pokud jde o funkci $ z = f (x, y) $, zvažte pojmy obecné (úplné) a částečné přírůstky funkce.

Nechť je zadána funkce $ z = f (x, y) $ ze dvou nezávislých proměnných $ (x, y) $.

Poznámka 1

Protože proměnné $ (x, y) $ jsou nezávislé, jedna z nich se může měnit, zatímco druhá zůstává konstantní.

Pojďme dát proměnné $ x $ přírůstek $ \ Delta x $, při zachování hodnoty proměnné $ y $ beze změny.

Pak funkce $ z = f (x, y) $ obdrží přírůstek, který se bude nazývat částečný přírůstek funkce $ z = f (x, y) $ vzhledem k proměnné $ x $. Označení:

Podobně dáme proměnné $ y $ přírůstek $ \ Delta y $, přičemž ponecháme hodnotu proměnné $ x $ beze změny.

Pak funkce $ z = f (x, y) $ obdrží přírůstek, který se bude nazývat částečný přírůstek funkce $ z = f (x, y) $ vzhledem k proměnné $ y $. Označení:

Pokud je argumentu $ x $ zadán přírůstek $ \ Delta x $ a argument $ y $ - přírůstek $ \ Delta y $, pak je plný přírůstek dané funkce $ z = f (x, y) $ získané. Označení:

Máme tedy:

$ \ Delta _ (x) z = f (x + \ Delta x, y) -f (x, y) $ - částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ x $;

$ \ Delta _ (y) z = f (x, y + \ Delta y) -f (x, y) $ - částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ y $;

$ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x, y) $ - plný přírůstek funkce $ z = f (x, y) $.

Příklad 1

Rozhodnutí:

$ \ Delta _ (x) z = x + \ Delta x + y $ - částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ x $;

$ \ Delta _ (y) z = x + y + \ Delta y $ je částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ y $.

$ \ Delta z = x + \ Delta x + y + \ Delta y $ - plný přírůstek funkce $ z = f (x, y) $.

Příklad 2

Vypočítejte podíl a celkový přírůstek funkce $ z = xy $ v bodě $ (1; 2) $ pro $ \ Delta x = 0,1; \, \, \ Delta y = 0,1 $.

Rozhodnutí:

Podle definice soukromého přírůstku zjistíme:

$ \ Delta _ (x) z = (x + \ Delta x) \ cdot y $ - částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ x $

$ \ Delta _ (y) z = x \ cdot (y + \ Delta y) $ - částečný přírůstek funkce $ z = f (x, y) $ vzhledem k $ y $;

Podle definice celého přírůstku najdeme:

$ \ Delta z = (x + \ Delta x) \ cdot (y + \ Delta y) $ - plný přírůstek funkce $ z = f (x, y) $.

Proto,

\ [\ Delta _ (x) z = (1 + 0,1) \ cdot 2 = 2,2 \] \ [\ Delta _ (y) z = 1 \ cdot (2 + 0,1) = 2,1 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) = 1,1 \ cdot 2,1 = 2,31. \]

Poznámka 2

Celkový přírůstek dané funkce $ z = f (x, y) $ se nerovná součtu jejích dílčích přírůstků $ \ Delta _ (x) z $ a $ \ Delta _ (y) z $. Matematická notace: $ \ Delta z \ ne \ Delta _ (x) z + \ Delta _ (y) z $.

Příklad 3

Zkontrolujte funkci poznámky k tvrzení

Rozhodnutí:

$ \ Delta _ (x) z = x + \ Delta x + y $; $ \ Delta _ (y) z = x + y + \ Delta y $; $ \ Delta z = x + \ Delta x + y + \ Delta y $ (získané v příkladu 1)

Najděte součet dílčích přírůstků dané funkce $ z = f (x, y) $

\ [\ Delta _ (x) z + \ Delta _ (y) z = x + \ Delta x + y + (x + y + \ Delta y) = 2 \ cdot (x + y) + \ Delta x + \ Delta y. \]

\ [\ Delta _ (x) z + \ Delta _ (y) z \ ne \ Delta z. \]

Definice 2

Pokud je pro každou trojici $ (x, y, z) $ hodnot tří nezávislých proměnných z určité oblasti přidružena určitá hodnota $ w $, pak se říká, že $ w $ je funkcí tří proměnných $ ( x, y, z) $ v této oblasti.

Označení: $ w = f (x, y, z) $.

Definice 3

Pokud je pro každou kolekci $ (x, y, z, ..., t) $ hodnot nezávislých proměnných z určité oblasti přidružena určitá hodnota $ w $, pak se říká, že $ w $ je funkce proměnných $ (x, y, z, ..., t) $ v této doméně.

Zápis: $ w = f (x, y, z, ..., t) $.

Pro funkci tří nebo více proměnných se stejným způsobem jako pro funkci dvou proměnných stanoví dílčí přírůstky pro každou z proměnných:

$ \ Delta _ (z) w = f (x, y, z + \ Delta z) -f (x, y, z) $ - částečný přírůstek funkce $ w = f (x, y, z, .. ., t) $ o $ z $;

$ \ Delta _ (t) w = f (x, y, z, ..., t + \ Delta t) -f (x, y, z, ..., t) $ - částečný přírůstek funkce $ w = f (x, y, z, ..., t) $ o $ t $.

Příklad 4

Napište podíl a celkový přírůstek funkce

Rozhodnutí:

Podle definice soukromého přírůstku zjistíme:

$ \ Delta _ (x) w = ((x + \ Delta x) + y) \ cdot z $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ x $

$ \ Delta _ (y) w = (x + (y + \ Delta y)) \ cdot z $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ y $;

$ \ Delta _ (z) w = (x + y) \ cdot (z + \ Delta z) $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ z $;

Podle definice celého přírůstku najdeme:

$ \ Delta w = ((x + \ Delta x) + (y + \ Delta y)) \ cdot (z + \ Delta z) $ - plný přírůstek funkce $ w = f (x, y, z) $ .

Příklad 5

Vypočítejte podíl a celkový přírůstek funkce $ w = xyz $ v bodě $ (1; 2; 1) $ za $ \ Delta x = 0,1; \, \, \ Delta y = 0,1; \, \, \ Delta z = 0,1 $.

Rozhodnutí:

Podle definice soukromého přírůstku zjistíme:

$ \ Delta _ (x) w = (x + \ Delta x) \ cdot y \ cdot z $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ x $

$ \ Delta _ (y) w = x \ cdot (y + \ Delta y) \ cdot z $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ y $;

$ \ Delta _ (z) w = x \ cdot y \ cdot (z + \ Delta z) $ - částečný přírůstek funkce $ w = f (x, y, z) $ vzhledem k $ z $;

Podle definice celého přírůstku najdeme:

$ \ Delta w = (x + \ Delta x) \ cdot (y + \ Delta y) \ cdot (z + \ Delta z) $ - plný přírůstek funkce $ w = f (x, y, z) $.

Proto,

\ [\ Delta _ (x) w = (1 + 0,1) \ cdot 2 \ cdot 1 = 2,2 \] \ [\ Delta _ (y) w = 1 \ cdot (2 + 0,1) \ cdot 1 = 2,1 \] \ [\ Delta _ (y) w = 1 \ cdot 2 \ cdot (1 + 0,1) = 2,2 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) \ cdot (1 + 0,1) = 1,1 \ cdot 2,1 \ cdot 1,1 = 2,541. \]

Z geometrického hlediska je celkový přírůstek funkce $ z = f (x, y) $ (podle definice, $ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x , y) $) se rovná přírůstku funkce plot aplikace $ z = f (x, y) $ při přechodu z bodu $ M (x, y) $ do bodu $ M_ (1) (x + \ Delta x , y + \ Delta y) $ (obr. 1).

Obrázek 1.