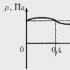
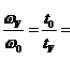روش محدودیت بولی در تحلیل کیفی سیستم های دینامیکی باینری. تحلیل کیفی سیستم های دینامیکی

سینتیک فرآیندهای بیولوژیکی

چگونه می توان پویایی سیستم های بیولوژیکی را توصیف کرد؟ در هر لحظه از زمان، یک سیستم بیولوژیکی دارای مجموعه ای از ویژگی های خاص است. به عنوان مثال، با مشاهده جمعیت یک گونه، می توان اندازه آن، مساحت قلمرو اشغال شده، مقدار غذای موجود، دمای محیط و غیره را ثبت کرد. سیر یک واکنش شیمیایی را می توان با غلظت مشخص کرد. از مواد درگیر، فشار، دما و سطح اسیدی محیط. مجموعه مقادیر تمام ویژگی هایی که محقق برای توصیف سیستم انتخاب کرده است، وضعیت سیستم در هر لحظه از زمان است. هنگام ایجاد یک مدل، متغیرها و پارامترها در مجموعه مشخص شده انتخاب می شوند. متغیرها مقادیری هستند که تغییرات آنها در درجه اول مورد توجه محقق است، پارامترها شرایط "محیط خارجی" هستند. برای متغیرهای انتخاب شده است که معادلاتی جمع آوری می شود که الگوهای تغییر در سیستم را در طول زمان منعکس می کند. به عنوان مثال، هنگام ایجاد مدلی برای رشد یک کشت میکروبی، معمولاً از تعداد آن به عنوان یک متغیر و از نرخ تولید مثل به عنوان یک پارامتر استفاده می شود. ممکن است دمایی که در آن رشد رخ می دهد قابل توجه باشد، سپس این شاخص نیز به عنوان پارامتر در مدل گنجانده شده است. و اگر به عنوان مثال سطح هوادهی همیشه کافی باشد و تاثیری در فرآیندهای رشد نداشته باشد، اصلاً در مدل گنجانده نشده است. به عنوان یک قاعده، پارامترها در طول آزمایش بدون تغییر باقی می مانند، با این حال، شایان ذکر است که همیشه اینطور نیست.

می توان پویایی یک سیستم بیولوژیکی (یعنی تغییر حالت آن در طول زمان) را با استفاده از هر دو مدل گسسته و پیوسته توصیف کرد. مدل های گسسته فرض می کنند که زمان یک کمیت گسسته است. این مربوط به ثبت مقادیر متغیرها در فواصل زمانی مشخص (به عنوان مثال، یک بار در ساعت یا یک بار در سال) است. در مدل های پیوسته، یک متغیر بیولوژیکی تابعی پیوسته از زمان است که به عنوان مثال نشان داده می شود: ایکس(تی).

اغلب اهمیت زیادی دارد شرایط اولیهمدل ها - وضعیت مشخصه مورد مطالعه در لحظه اولیه زمان، یعنی. در تی = 0.

هنگام مطالعه تغییر مداوم برخی از ویژگی ها ایکس(تی) ممکن است اطلاعاتی در مورد میزان تغییر آن بدانیم. این اطلاعات را می توان به طور کلی به صورت یک معادله دیفرانسیل نوشت:

چنین نماد رسمی به این معنی است که سرعت تغییر برخی از ویژگی های مورد مطالعه تابع زمان و بزرگی این ویژگی است.

اگر سمت راست یک معادله دیفرانسیل شکل به صراحت به زمان بستگی نداشته باشد، به عنوان مثال. نمایشگاه:

سپس این معادله نامیده می شود خود مختار(سیستم توصیف شده توسط چنین معادله ای نامیده می شود خود مختار). وضعیت سیستم های مستقل در هر لحظه از زمان با یک مقدار مشخص می شود - مقدار متغیر ایکسدرحال حاضر تی.

اجازه دهید از خود یک سوال بپرسیم: اجازه دهید یک معادله دیفرانسیل برای آن داده شود ایکس(تیآیا می توان همه توابع را پیدا کرد ایکس(تی) ارضای این معادله؟ یا: اگر مقدار اولیه یک متغیر مشخص مشخص باشد (مثلاً اندازه اولیه یک جمعیت، غلظت یک ماده، رسانایی الکتریکی محیط و غیره) و اطلاعاتی در مورد ماهیت تغییر در آن وجود داشته باشد. این متغیر، آیا می توان پیش بینی کرد که مقدار آن در تمام مقاطع زمانی بعدی چقدر خواهد بود؟ پاسخ سوال مطرح شده به این صورت است: اگر شرایط اولیه برای معادله داده شود و شرایط قضیه کوشی برآورده شود (تابع داده شده در یک منطقه معین و مشتق جزئی آن در این ناحیه پیوسته هستند)، آنگاه وجود دارد. یک راه حل منحصر به فرد از معادله است که شرایط اولیه داده شده را برآورده می کند. (به یاد بیاورید که هر تابع پیوسته ای که معادله دیفرانسیل را برآورده کند، راه حل آن معادله نامیده می شود.) این بدان معنی است که اگر ویژگی های حالت اولیه آن مشخص باشد و معادله مدل شرایط را برآورده کند، می توانیم رفتار یک سیستم بیولوژیکی را به طور منحصر به فرد پیش بینی کنیم. قضیه کوشی.

حالت ساکن پایداری

ما معادله دیفرانسیل خودمختار را در نظر خواهیم گرفت

در حالت ثابت، مقادیر متغیرها در سیستم با گذشت زمان تغییر نمی کند، یعنی میزان تغییر در مقادیر متغیرها 0: . اگر سمت چپ معادله (1.2) برابر با صفر باشد، سمت راست نیز برابر با صفر است: . ریشه های این معادله جبری هستند حالت های ساکنمعادله دیفرانسیل (1.2).

مثال 1.1:حالات ثابت معادله را بیابید.

راه حل: اصطلاحی را که مشتق را در بر نمی گیرد به سمت راست برابری منتقل می کنیم: . طبق تعریف، در حالت ساکن، برابری زیر برقرار است: . پس برابری باید برقرار باشد . معادله را حل می کنیم:

,

بنابراین، معادله دارای 3 حالت ثابت است: , .

سیستم های بیولوژیکی دائماً تأثیرات خارجی مختلف و نوسانات متعددی را تجربه می کنند. در همان زمان، آنها (سیستم های بیولوژیکی) هموستاز دارند، یعنی. مقاوم. در زبان ریاضی به این معنی است که متغیرها با انحرافات کوچک به مقادیر ثابت خود باز می گردند. آیا این رفتار یک سیستم بیولوژیکی در مدل ریاضی آن منعکس خواهد شد؟ آیا حالت های ثابت مدل پایدار است؟

حالت ثابت است پایدار، اگر برای یک انحراف به اندازه کافی کوچک از موقعیت تعادل، سیستم هرگز از نقطه منفرد دور نخواهد شد. حالت پایدار مربوط به حالت پایدار عملکرد سیستم است.

حالت تعادل یک معادله لیاپانوف پایدار است اگر برای هر کسی همیشه بتوان به گونه ای پیدا کرد که اگر , پس برای همه .

یک روش تحلیلی برای مطالعه پایداری یک حالت ثابت وجود دارد - روش لیاپانوف. برای اثبات آن، یادآوری می کنیم فرمول تیلور.

اگر به صورت آزاد صحبت کنیم، فرمول تیلور رفتار یک تابع را در مجاورت یک نقطه مشخص نشان می دهد. اجازه دهید یک تابع دارای مشتقات در یک نقطه از تمام سفارشات تا n-فراگیر. سپس فرمول تیلور برای:

با کنار گذاشتن عبارت باقیمانده، که خود یک عدد بینهایت کوچک از مرتبه بالاتر است، فرمول تقریبی تیلور را بدست می آوریم:

سمت راست فرمول تقریبی نامیده می شود چند جمله ای تیلورتوابع، آن را به عنوان نشان داده شده است.

مثال 1.2:تابع را در یک سری تیلور در همسایگی یک نقطه تا مرتبه 4 گسترش دهید.

راه حل:سری تیلور را تا مرتبه چهارم به صورت کلی می نویسیم:

مشتقات تابع داده شده را در نقطه زیر بیابید:

,

مقادیر به دست آمده را با فرمول اصلی جایگزین کنید:

یک روش تحلیلی برای مطالعه پایداری یک حالت ساکن ( روش لیاپانوف) به شرح زیر است. اجازه دهید حالت ساکن معادله باشد. بیایید یک انحراف کوچک از متغیر را تنظیم کنیم ایکساز مقدار ثابت آن: , جایی که . عبارت را جایگزین نقطه کنید ایکسبه معادله اصلی: . سمت چپ معادله به شکل زیر خواهد بود: ، از آنجایی که در حالت ساکن نرخ تغییر مقدار متغیر برابر با صفر است: . ما سمت راست را به یک سری تیلور در مجاورت حالت ساکن گسترش می دهیم، با در نظر گرفتن این که، فقط عبارت خطی را در سمت راست معادله باقی می گذاریم:

اخذ شده معادله خطی شدهیا معادله تقریبی اول. مقدار مقداری ثابت است، آن را نشان دهید آ: . جواب کلی معادله خطی شده به صورت زیر است: . این عبارت قانونی را توصیف می کند که طبق آن انحراف از حالت ساکن ارائه شده توسط ما در زمان تغییر می کند. انحراف به مرور زمان از بین می رود، یعنی. در، اگر توان در توان منفی باشد، i.e. . طبق تعریف، حالت پایدار خواهد بود پایدار. اگر با افزایش زمان، انحراف فقط افزایش می یابد، حالت ساکن است ناپایدار. در موردی که معادله تقریب اول نمی تواند پاسخی به سوال پایداری حالت ساکن بدهد. لازم است در بسط سری تیلور اصطلاحات مرتبه بالاتر در نظر گرفته شود.

علاوه بر روش تحلیلی مطالعه پایداری یک حالت ساکن، یک روش گرافیکی نیز وجود دارد.

مثال 1.3.اجازه دهید . حالات ثابت معادله را بیابید و با استفاده از نمودار تابع نوع پایداری آنها را تعیین کنید .

راه حل:بیایید نکات ویژه ای را پیدا کنیم:

,

,

ما یک نمودار از تابع می سازیم (شکل 1.1).

برنج. 1.1. نمودار تابع (مثال 1.3).

اجازه دهید از نمودار مشخص کنیم که آیا هر یک از حالت های ثابت یافت شده پایدار هستند یا خیر. بیایید یک انحراف کوچک از نقطه نماینده از نقطه مفرد به سمت چپ تنظیم کنیم: . در نقطه ای با مختصات، تابع یک مقدار مثبت می گیرد: یا . آخرین نابرابری به این معنی است که با گذشت زمان باید مختصات افزایش یابد، یعنی نقطه نماینده باید به نقطه برگردد. حال بیایید یک انحراف کوچک از نقطه نماینده از نقطه مفرد به سمت راست تنظیم کنیم: . در این ناحیه، تابع مقدار مثبت را حفظ می کند، بنابراین، با گذشت زمان، مختصات ایکسهمچنین افزایش می یابد، یعنی نقطه نماینده از نقطه دور می شود. بنابراین، یک انحراف کوچک سیستم را از حالت ساکن خارج می کند، بنابراین، طبق تعریف، نقطه منفرد ناپایدار است. استدلال مشابه منجر به این واقعیت می شود که هر انحراف از نقطه منفرد با گذشت زمان از بین می رود، حالت ساکن پایدار است. انحراف نقطه نشان دهنده در هر جهت از حالت ساکن منجر به حذف آن از نقطه می شود، این یک حالت ساکن ناپایدار است.

حل سیستم معادلات دیفرانسیل خطی

اجازه دهید به مطالعه سیستم های معادلات، اول خطی بپردازیم. به طور کلی، سیستم معادلات دیفرانسیل خطی را می توان به صورت زیر نشان داد:

تجزیه و تحلیل سیستم معادلات با یافتن حالت های ساکن آغاز می شود. برای سیستم های شکل (1.3)، نقطه مفرد منحصر به فرد است، مختصات آن (0،0) است. استثنا مورد منحط است، زمانی که معادلات را می توان به صورت زیر نشان داد:

(1.3*)

در این حالت، تمام جفت هایی که رابطه را ارضا می کنند، نقاط ثابت سیستم هستند (1.3*). به طور خاص، نقطه (0,0) نیز برای سیستم (1.3*) ثابت است. در صفحه فاز، در این مورد، ما یک خط مستقیم با ضریب شیب داریم که از مبدا می گذرد، که هر نقطه آن یک نقطه منفرد از سیستم (1.3 *) است (جدول 1.1، مورد 6 را ببینید).

سوال اصلی که نتیجه مطالعه یک سیستم معادلات باید به آن پاسخ داده شود این است که آیا حالت ساکن سیستم پایدار است و این جواب چه ویژگی دارد (یکنواخت یا غیر یکنواخت).

تصمیم مشترکسیستم دو معادله خطی به شکل زیر است:

اعداد مشخصهرا می توان بر حسب ضرایب معادلات خطی به صورت زیر بیان کرد:

اعداد مشخصه می توانند 1) واقعی نشانه های مختلف، 2) واقعی یک علامت، 3) مزدوج مختلط، و همچنین، در موارد منحط، 4) کاملاً خیالی، 5) واقعی منطبق، 6) واقعی باشند که یکی از آنها (یا) هر دو) برابر با صفر است. این موارد نوع رفتار راه حل را برای یک سیستم معادلات دیفرانسیل معمولی تعیین می کند. پرتره های فاز مربوطه در جدول 1.1 ارائه شده است.

جدول 1.1. انواع حالت های ساکن یک سیستم از دو معادله دیفرانسیل خطی و پرتره های فاز مربوطه. فلش ها جهت حرکت نقطه نماینده را نشان می دهد

ساخت پرتره های فاز و جنبشی یک سیستم دو معادله دیفرانسیل خطی

صفحه فازصفحه ای با محورهای مختصاتی که مقادیر متغیرها بر روی آن رسم می شود نامیده می شود ایکسو y، هر نقطه از صفحه مربوط به حالت خاصی از سیستم است. مجموعه نقاطی در صفحه فاز که موقعیت آنها مطابق با حالات سیستم در فرآیند تغییر متغیرها در زمان است، با توجه به معادلات داده شده سیستم مورد مطالعه، نامیده می شود. مسیر فاز. مجموعه مسیرهای فاز برای مقادیر اولیه متفاوت متغیرها یک پرتره از سیستم را ارائه می دهد. ساختمان پرتره فازبه شما امکان می دهد در مورد ماهیت تغییرات در متغیرها نتیجه گیری کنید ایکسو yبدون دانستن جواب های تحلیلی سیستم معادلات اولیه.

سیستمی از معادلات دیفرانسیل خطی را در نظر بگیرید:

ساخت پرتره فاز با ساخت شروع می شود ایزوکلین های اصلی(ایزوکلاین خطی است که در سراسر آن شیب منحنی فاز (مسیر) تعیین شده توسط معادله ثابت می ماند). برای یک سیستم از دو معادله دیفرانسیل خطی، اینها همیشه خطوط مستقیمی هستند که از مبدا عبور می کنند. معادله خطوط همسان مماس های افقی: . معادله ایزوکلاین مماس های عمودی: . برای ساخت بیشتر پرتره فاز، ساخت هم‌زمان از مماس‌هایی که در یک زاویه عبور می‌کنند مفید است. برای یافتن معادله ایزوکلاین مربوطه باید معادله را حل کرد . همچنین با استفاده از مقادیر تقریبی مماس زوایا می‌توانید هم‌زمان‌های مماس زوایای دیگر را پیدا کنید. پاسخ به این سوال که مسیرهای فاز در چه زاویه ای باید محورهای مختصات را قطع کنند نیز می تواند در ساخت پرتره فاز کمک کند. برای انجام این کار، در معادله ایزوکلاین برابری های مربوطه را (برای تعیین زاویه تقاطع با محور OY) و (برای تعیین زاویه تقاطع با محور OX) جایگزین می کنیم.

مثال 1.4.نوع نقطه منفرد سیستم معادلات خطی را تعیین کنید:

یک پرتره فاز و جنبشی از سیستم بسازید.

راه حل:مختصات نقطه مفرد (0,0) است. ضرایب معادلات خطی عبارتند از: , , , . اجازه دهید نوع حالت ثابت را تعریف کنیم (به بخش اعداد مشخصه مراجعه کنید):

بنابراین، ریشه های مشخصه خیالی هستند: بنابراین، نقطه منفرد سیستم خطی در نظر گرفته شده دارای نوع مرکزی است (شکل 1.2a).

معادله ایزوکلاین مماس های افقی: , معادله ایزوکلاین مماس های عمودی: . در زاویه 45 درجه، مسیرهای سیستم یک خط مستقیم را قطع می کنند .

پس از ساخت پرتره فاز، لازم است جهت حرکت در طول مسیرهای پیدا شده تعیین شود. این کار را می توان به روش زیر انجام داد. در هر مسیری یک نقطه دلخواه بگیرید. به عنوان مثال، در ایزوکلاین مماس های افقی (1،1). اجازه دهید مختصات این نقطه را در سیستم معادلات جایگزین کنیم. ما عباراتی را برای نرخ تغییر متغیرها به دست می آوریم ایکس,yدر این مرحله:

مقادیر به دست آمده میزان تغییر متغیر را نشان می دهد ایکس- منفی، یعنی مقدار آن باید کاهش یابد و متغیر yتغییر نمی کند. جهت دریافتی را با فلش مشخص می کنیم. بنابراین، در مثال مورد بررسی، حرکت در طول مسیرهای فاز در خلاف جهت عقربه های ساعت هدایت می شود. با جایگزینی مختصات نقاط مختلف در سیستم، می توانید یک "نقشه" از جهت سرعت ها، به اصطلاح، دریافت کنید. میدان برداری.

شکل 1.2. پرتره فاز (الف) و جنبشی (ب) سیستم، مثال 1.4

توجه داشته باشید که در ایزوکلاین مماس های افقی متغیر yدر یک مسیر معین به حداکثر یا حداقل مقدار خود می رسد. برعکس، بر روی ایزوکلاین مماس های عمودی، متغیر ایکس.

ایجاد یک پرتره جنبشی از سیستم به معنای ترسیم وابستگی مقادیر متغیرها است. ایکس,yاز زمان. یک پرتره فاز می تواند برای ساختن یک پرتره جنبشی و بالعکس استفاده شود. مسیر یک فاز مربوط به یک جفت منحنی جنبشی است. اجازه دهید یک نقطه دلخواه را در پرتره فاز در یک مسیر فاز دلخواه انتخاب کنیم. این نقطه شروع مربوط به زمان است. بسته به جهت حرکت در سیستم مورد نظر، مقادیر متغیرها ایکس,yیا کاهش یا افزایش. مختصات نقطه شروع را بگذارید (1،1). با توجه به پرتره فاز ساخته شده، با شروع از این نقطه، باید در خلاف جهت عقربه های ساعت، مختصات حرکت کنیم. ایکسو yدر حالی که کاهش خواهند یافت. با گذشت زمان، مختصات ایکساز مقدار 0 عبور می کند yدر حالی که مثبت باقی می ماند. مختصات بیشتر ایکسو yبه کاهش ادامه دهید، مختصات yاز 0 عبور می کند (مقدار ایکسدر حالی که منفی است). مقدار ایکسبه حداقل مقدار خود در ایزوکلاین مماس های عمودی می رسد، سپس شروع به افزایش می کند. مقدار yبه حداقل مقدار خود در هم‌زمان مماس‌های افقی می‌رسد (مقدار ایکسدر این مقطع زمانی منفی است). بعد، و مقدار ایکس، و ارزش yافزایش، بازگشت به مقادیر اولیه (شکل 1.2b).

بررسی پایداری حالت های ساکن سیستم های غیرخطی مرتبه دوم

اجازه دهید یک سیستم بیولوژیکی با یک سیستم از دو معادله دیفرانسیل مرتبه دوم مستقل با یک شکل کلی توصیف شود:

مقادیر ثابت متغیرهای سیستم از معادلات جبری تعیین می شود:

در همسایگی هر حالت ساکن می توان در نظر گرفت اولین سیستم تقریب(سیستم خطی) که مطالعه آن می تواند پاسخ به سوال پایداری نقطه منفرد و ماهیت مسیرهای فاز در همسایگی کوچک آن را ممکن سازد.

خارج از

ما داریم ، نقطه مفرد خشن است. ریشه های مشخصه سیستم تقریب اول برابر است، هر دو واقعی و منفی هستند، بنابراین، در مجاورت نقطه منفرد صفر، رفتار مسیرهای فاز سیستم با نوع گره پایدار مطابقت دارد.

اتوماسیون و تله مکانیک، L-1، 2007

RAS B 02.70.-c, 47.ll.-j

© 2007 Yu.S. پاپکوف، دکتر فن. Sci. (موسسه تحلیل سیستم RAS، مسکو)

تجزیه و تحلیل کیفی سیستم های دینامیک با اپراتور Vd-ENTROPY

روشی برای مطالعه وجود، منحصر به فرد بودن و محلی سازی نقاط منفرد کلاس در نظر گرفته شده DSEE پیشنهاد شده است. شرایط ثبات "در کوچک" و "در بزرگ" به دست می آید. نمونه هایی از کاربرد شرایط به دست آمده آورده شده است.

1. مقدمه

بسیاری از مسائل مدل‌سازی ریاضی فرآیندهای دینامیکی را می‌توان بر اساس مفهوم سیستم‌های دینامیکی با عملگر آنتروپی (DEOS) حل کرد. DSEE یک سیستم پویا است که در آن غیرخطی بودن با مسئله پارامتری حداکثر سازی آنتروپی توصیف می شود. از نظر Feio-moyological، DSEO مدلی از یک کلان سیستم با بازتولید "آهسته" خود و تخصیص "سریع" منابع است. برخی از ویژگی‌های DSEO مورد مطالعه قرار گرفت. این کار چرخه مطالعات ویژگی های کیفی DSEO ها را ادامه می دهد.

ما یک سیستم دینامیکی با عملگر آنتروپی Vd در نظر می گیریم:

^ = £(x، y(x))، x e En:

y(x) = a^max(Hv(y) | Ty = u(x)، y e E^) > 0.

در این عبارات:

C(x، y)، u(x) توابع برداری پیوسته قابل تمایز هستند.

آنتروپی

(1.2) Hv (y) = uz 1n به عنوان > 0، s = T~m;

T - (r x w) -ماتریس با عناصر ^ 0 دارای رتبه کل برابر با r است.

تابع برداری u(x) به طور پیوسته قابل تمایز است، مجموعه

(1.3) Q = (q: 0<оТ ^ ц ^ а+} С Е+,

که در آن a- و a + بردارهایی از E+ هستند، جایی که a- بردار با اجزای کوچک است.

استفاده از نمایش معروف عملگر آنتروپی بر حسب ضریب لاگرانژ. سیستم (1.1) را به شکل زیر تبدیل می کنیم:

- = £(x، y(z))، x e Kn، y(z) e K?، r e Er+

Uz (r) \u003d az\\ ^, 3 \u003d 1, m-

O(x، z) = Ty(z) = q(x)،

که در آن rk = exp(-Ak) > 0 ضرب کننده های نمایی لاگرانژ هستند.

همراه با DSEE فرم کلی (1.1)، ما به دنبال طبقه بندی ارائه شده در .

DSEE با جریان قابل تفکیک:

(1-5) ^ = I (x) + Vy (z)،

که در آن B (n x m) -ماتریس.

DSEO با جریان ضربی:

(1.6) ^ = x ® (a - x ® Xu(r))، ab

که در آن W یک ماتریس (n x m) با عناصر غیر منفی است، a یک بردار با مولفه های مثبت است، ® علامت ضرب مختصات است.

هدف این مقاله بررسی وجود، منحصربه‌فرد بودن و محلی‌سازی نقاط منفرد DSEE و پایداری آن‌ها است.

2. نقاط مفرد

2.1. وجود داشتن

سیستم (1.4) را در نظر بگیرید. نقاط منفرد این سیستم دینامیکی با معادلات زیر تعیین می شود:

(2.1) C^(x، y(z))=0، r = TP;

(2.2) uz(r) = a^ r^، 3 = T^:

(2.3) bk(r) = ^as r^ = dk(x)، k = 1,r.

ابتدا سیستم کمکی معادلات را در نظر بگیرید:

(2.4) C(q، z) = r، q e R،

که در آن مجموعه R با برابری (1.3) تعریف می شود و C(q, r) یک تابع برداری با مولفه ها است.

(2.5) Sk(d، r) = - Ok(r)، a-< дк < а+, к =1,г.

معادله (2.4) یک راه حل منحصر به فرد r* برای هر بردار ثابت q دارد که از ویژگی های عملگر آنتروپی Vg می آید (نگاه کنید به ).

از تعریف اجزای تابع برداری С(g, z) تخمین واضح صورت می گیرد:

(2.6) C(a+, r)< С(д, г) < С(а-,г), г в Е+. Рассмотрим два уравнения:

حل معادله اول را با r+ و دومی را با r- نشان می دهیم. تعریف کنیم

(2.7) C (a+,z) = z, C(a

(2.8) zmaX = حداکثر z+، zmin = mm zk

و بردارهای r بعدی

(2.9) z(zmax، zmax)، z(zmin، zmin).

لم 2.1. برای همه حل های q G Q (1. 3) z*(q) معادله (2.4) متعلق به بردار 1 قطعه است.

zmin< z*(q) < zmax,

که در آن بردارهای zmin و zmax با عبارات (2.7)-(2.9) تعریف می شوند.

اثبات قضیه در پیوست آورده شده است. Qq

qk(x) (1.3) برای x G Rn، سپس داریم

نتیجه 2.1. اجازه دهید شرایط لما 2.1 برآورده شود و توابع qk(x) شرایط (1.3) را برای همه ex x G Rn برآورده کنند. سپس برای تمام x G Rm راه حل های z* معادله (2.3) متعلق به بخش برداری است

zmin< z* < zmax

حال به معادلات (2.2) بازگردیم. که اجزای تابع برداری y(z) را تعیین می کند. عناصر ژاکوبین آن فرم دارد

(2.10) jb aj zk JJ & > 0

برای همه z G R+ به جز 0 و g. بنابراین، تابع برداری y(z) به شدت یکنواخت در حال افزایش است. طبق Lemma 2.1، از پایین و بالا محدود شده است، یعنی: برای همه z G Rr (از این رو برای همه x G Rn) مقادیر آن متعلق به مجموعه است

(2.11) Y = (y: y-< y < y+},

که در آن اجزای بردارهای yk، y+ با عبارات زیر تعیین می شوند:

(2.12) yk = aj y+ = aj znlax، j = h™.

(2.13) bj = Y، tsj، 3 =1،

معادله اول (2.1) را در نظر بگیرید و آن را به صورت زیر بنویسید:

(2.14) L(x، y) = 0 برای همه y e Y ⊂ E^.

این معادله وابستگی متغیر x را به متغیر y متعلق به Y تعیین می کند

ما (1.4) را به وجود یک تابع ضمنی x(y) کاهش می دهد که با معادله (2.14) تعریف شده است.

لم 2.2. اجازه دهید شرایط زیر برآورده شود:

الف) تابع برداری L(x,y) در مجموعه متغیرها پیوسته است.

ب) lim L(x, y) = ±<ж для любого фиксированного у е Y;

ج) det J (x, y) = 0 برای همه ex x e En برای هر y e Y ثابت.

سپس یک تابع ضمنی منحصر به فرد x*(y) بر روی Y تعریف شده است. در این لم، J(x, y) ژاکوبین با عناصر است.

(2.15) Ji,i (x,y) = --i, i,l = l,n.

اثبات در ضمیمه آورده شده است. از لم های فوق بر می آید

قضیه 2.1. بگذارید شرایط Lemmas 2.1 و 2.2 برآورده شود. سپس یک نقطه منحصر به فرد از DSEE (1.4) و بر این اساس، (1.1) وجود دارد.

2.2. بومی سازی

مطالعه محلی سازی یک نقطه منفرد به عنوان امکان ایجاد فاصله ای که در آن قرار دارد درک می شود. این کار خیلی ساده نیست، اما برای برخی از کلاس های DSEE می توان چنین فاصله ای را ایجاد کرد.

اجازه دهید به اولین گروه از معادلات در (2.1) بپردازیم و آنها را به شکل نمایش دهیم

(2.16) L(x,y)=0، y-y y y+،

که در آن y- و y+ با برابری های (2.12)، (2.13) تعریف می شوند.

قضیه 2.2. اجازه دهید تابع برداری L(x,y) به طور پیوسته قابل تفکیک و به طور یکنواخت در هر دو متغیر افزایش یابد، یعنی.

--> 0، --> 0; i,l = 1, n; j = 1، m. dxi dyj

سپس جواب سیستم (2.16) نسبت به متغیر x متعلق به بازه (2.17) xmin x x x xmax است.

الف) بردارهای xmin، xmax شکل دارند

حداقل \u003d i x 1 xmax \u003d r x t;

\xmin: . ..، xminlxmax، . . .، xmax) :

xmin - ^Qin ^ ■ , xmax - ^QaX ^ ;

6) x- و x+ - اجزای حل معادلات زیر

(2.19) L(x,y-)=0, L(x,y+) = 0

البته با oo m

اثبات قضیه در پیوست آورده شده است.

3. پایداری DSEA "در کوچک"

3.1. DSEE با جریان قابل تفکیک اجازه دهید به معادلات DSEE با جریان قابل تفکیک بپردازیم و آنها را به شکل زیر ارائه کنیم:

- \u003d / (x) + Bu (r (x))، x e Kp ab

Y- (r (X)) \u003d azP (X) Y33، 3 \u003d 1، "~ 8 \u003d 1

0(x، r(x)) = Ty(r(x)) = q(x)، r e Hr.

در اینجا مقادیر اجزای تابع برداری q(x) متعلق به مجموعه Q (1.3) است، ماتریس (n × w) B دارای رتبه کل برابر با n (n) است.< ш). Вектор-функция / (х) непрерывно дифференцируемая.

اجازه دهید سیستم مورد بررسی یک نقطه منفرد x داشته باشد. برای مطالعه پایداری این نقطه منفرد "در کوچک" یک سیستم خطی می سازیم

که در آن A یک ماتریس (n x n) است که عناصر آن در نقطه x محاسبه می شوند و بردار t = x - x. با توجه به معادله اول در (3.1)، ماتریس سیستم خطی شده است

A \u003d 7 (x) + BUg (g) Xx (x)، x \u003d g (x)،

| 3 \u003d 1، w، k \u003d 1،

I k \u003d 1, g, I \u003d 1, p

از (3.1) عناصر ماتریس Yr:dy تعیین می شوند.

"bkz P" 8=1

3، r8 x8، 5 1، r.

برای تعیین عناصر ماتریس Zx به آخرین گروه از معادلات در (3.1) می پردازیم. B نشان می دهد که این معادلات یک تابع بردار ضمنی r(x) را تعریف می کنند، که اگر تابع برداری g(x) به طور پیوسته قابل تمایز باشد، پیوسته قابل تمایز است. Zx ژاکوبین تابع برداری z(x) با معادله تعریف می شود

<Эг (z)Zx(Х) = Qx(Х),

vg (X) \u003d T Ug (X)،

ddk, -t-, - "- k \u003d 1, r, I \u003d 1, n dx \

از این معادله (3.9) Zx(x) = s-1(z)Qx(x) داریم.

جایگزینی این نتیجه به برابری (3.3). ما گرفتیم:

A \u003d 1 (x) + P (x)، P (x) \u003d VUg (g) [Tg (g)] -1 Qx (x).

بنابراین، معادله سیستم خطی شکل می گیرد

(c.i) | = (j+p)e

در اینجا، عناصر ماتریس های J، P در یک نقطه منفرد محاسبه می شوند. شرایط پایداری کافی "در کوچک" DSEE (3.1) با موارد زیر تعیین می شود

قضیه 3.1. DSEE (3.1) دارای یک نقطه منفرد x است که اگر شرایط زیر برآورده شود "در کوچک" پایدار است:

الف) ماتریس های J, P (3.10) سیستم خطی شده (3.11) دارای مقادیر ویژه واقعی و متفاوت هستند و ماتریس J دارای حداکثر مقدار ویژه است.

Pmax = حداکثر Pg > 0،

Wmax = maxUi< 0;

Umax + Ptah<

از این قضیه و برابری (3.10) برمی‌آید که برای نقاط مفرد که Qx(x) = 0 و (یا) برای X، = 0 و tkj ^ 1 برای همه ex k,j، شرایط کافی قضیه نیست. راضی.

3.2. DSEE با جریان ضربی معادلات (1.6) را در نظر بگیرید. ارائه آنها در قالب:

X ® (a - x ® Wy(z(x)))، x e Rn;

yj(z(x)) = aj ПZs(x)]isi" j = 1,m;

(ZL2) yj (z(x)) = a^<~"ts

Q(x، z(x)) = Ty(z(x)) = q(x)، z e R++.

سیستم های. خواهد داشت:

(3.13)

در این عبارت، دیاگ C] یک ماتریس مورب با عناصر مثبت a1،...، an، Yr، Zx ماتریس هایی هستند که با برابری های (3.4)-(3.7) تعریف می شوند.

ماتریس A را به شکل نمایش می دهیم

(3.14) A = دیاگ + P (x)،

(3.15) P(x) = -2xWYz(z)Zx(x).

نشان دهید: maxi ai = nmax و wmax حداکثر مقدار ویژه ماتریس P(x) است (3.15). سپس قضیه 3.1 برای DSEE (1.6) نیز معتبر است. (3.12).

4. پایداری DSEA "در بزرگ"

اجازه دهید به معادلات DESO (1.4) بپردازیم، که در آن مقادیر اجزای تابع برداری q(x) متعلق به مجموعه Q (1.3) است. در سیستم مورد بررسی، یک نقطه منفرد Z وجود دارد که بردارهای z(x) = z ^ z-> 0 و

y(x) = y(z) = y > y-> 0.

اجازه دهید بردارهای انحراف £، C، П را از نقطه مفرد معرفی کنیم: (4.1) £ = x - x، (= y - y، n = z - z.

ZHEZHERUN A.A., POKROVSKY A.V. - 2009

معرفی

از آنجایی که مفهوم یک سیستم دینامیکی غیرخطی به اندازه کافی غنی است که بتواند طیف بسیار وسیعی از فرآیندها را پوشش دهد که در آن رفتار آینده سیستم توسط گذشته تعیین می‌شود، روش‌های تحلیل توسعه‌یافته در این زمینه در زمینه‌های بسیار متنوعی مفید هستند.

دینامیک غیرخطی حداقل از سه طریق وارد ادبیات می شود. اول، مواردی وجود دارد که داده‌های تجربی در مورد تغییر در طول زمان یک یا چند کمیت با استفاده از تکنیک‌های مبتنی بر نظریه دینامیکی غیرخطی، با حداقل فرضیات در مورد معادلات اساسی که بر فرآیند تولید داده‌ها حاکم است، جمع‌آوری و تحلیل می‌شوند. یعنی موردی است که در آن فرد به دنبال یافتن همبستگی هایی در داده هایی است که می تواند توسعه یک مدل ریاضی را هدایت کند، نه اینکه ابتدا مدل را حدس بزند و سپس آن را با داده ها مقایسه کند.

ثانیاً، مواردی وجود دارد که می‌توان از تئوری دینامیکی غیرخطی برای بیان اینکه برخی از مدل‌های ساده شده باید ویژگی‌های مهم یک سیستم معین را نشان دهد، استفاده کرد، که به این معنی است که مدل توصیف‌کننده می‌تواند در طیف وسیعی از پارامترها ساخته و مطالعه شود. این اغلب منجر به مدل هایی می شود که تحت پارامترهای مختلف به طور کیفی متفاوت رفتار می کنند و نشان می دهد که یک منطقه رفتاری بسیار شبیه به رفتار مشاهده شده در سیستم واقعی از خود نشان می دهد. در بسیاری از موارد، رفتار مدل نسبت به تغییرات پارامترها کاملاً حساس است، بنابراین اگر بتوان پارامترهای مدل را در یک سیستم واقعی اندازه‌گیری کرد، مدل در این مقادیر رفتار واقعی از خود نشان می‌دهد و می‌توان مطمئن بود که مدل از آن استفاده می‌کند. ویژگی های اساسی سیستم

ثالثاً، مواردی وجود دارد که معادلات مدل بر اساس توضیحات دقیق فیزیک شناخته شده ساخته می شوند. سپس آزمایش‌های عددی می‌توانند اطلاعاتی در مورد متغیرهایی ارائه دهند که برای آزمایش‌های فیزیکی در دسترس نیستند.

بر اساس مسیر دوم، این کار امتداد کار قبلی من "مدل دینامیکی غیرخطی صنایع وابسته به هم" و همچنین اثر دیگری است (Dmitriev, 2015)

تمام تعاریف لازم و سایر اطلاعات نظری مورد نیاز در کار در صورت نیاز در فصل اول آمده است. در اینجا دو تعریف ارائه خواهد شد که برای افشای خود موضوع تحقیق ضروری است.

ابتدا اجازه دهید دینامیک سیستم را تعریف کنیم. بر اساس یکی از تعاریف، دینامیک سیستم یک رویکرد مدل سازی شبیه سازی است که به لطف روش ها و ابزارهای خود، به ارزیابی ساختار سیستم های پیچیده و دینامیک آنها کمک می کند (شترمن). شایان ذکر است که دینامیک سیستم نیز یک تکنیک مدل‌سازی است که برای بازآفرینی مدل‌های رایانه‌ای صحیح (از لحاظ دقت) برای سیستم‌های پیچیده برای استفاده در آینده به منظور ایجاد یک شرکت/سازمان کارآمدتر و همچنین بهبود روش‌های استفاده می‌شود. تعامل با این سیستم بیشتر نیاز به پویایی سیستم در مواجهه با مدل‌های استراتژیک بلندمدت ایجاد می‌شود، و همچنین شایان ذکر است که نسبتاً انتزاعی است.

صحبت از دینامیک دیفرانسیل غیرخطی، ما یک سیستم غیر خطی را در نظر خواهیم گرفت، که طبق تعریف، سیستمی است که در آن تغییر در نتیجه متناسب با تغییر پارامترهای ورودی نیست و در آن تابع تابع را توصیف می کند. وابستگی تغییر در زمان و موقعیت یک نقطه در فضا (بوئینگ، 2016).

بر اساس تعاریف فوق، مشخص می‌شود که این کار سیستم‌های دیفرانسیل غیرخطی مختلفی را در نظر می‌گیرد که تعامل شرکت‌ها را توصیف می‌کند و همچنین مدل‌های شبیه‌سازی که بر اساس آنها ساخته شده‌اند. بر این اساس هدف کار مشخص می شود.

بنابراین، هدف از این کار انجام یک تحلیل کیفی از سیستم‌های پویا است که تعامل شرکت‌ها را در اولین تقریب توصیف می‌کند و یک مدل شبیه‌سازی بر اساس آنها ایجاد می‌کند.

برای دستیابی به این هدف، وظایف زیر مشخص شد:

تعیین پایداری سیستم

ساخت پرتره های فازی.

یافتن مسیرهای یکپارچه سیستم ها

ساخت مدل های شبیه سازی

هر یک از این کارها به یکی از بخش های هر یک از فصل های اثر اختصاص خواهد یافت.

بر اساس تمرین، ساخت ساختارهای ریاضی بنیادی که به طور موثر دینامیک را در سیستم‌ها و فرآیندهای فیزیکی مختلف مدل‌سازی می‌کنند، نشان می‌دهد که مدل ریاضی مربوطه تا حدودی نشان‌دهنده نزدیکی به اصلی مورد مطالعه است، زمانی که ویژگی‌های مشخصه آن را می‌توان از خواص و ویژگی‌ها استخراج کرد. ساختارهایی از نوع حرکتی که دینامیک سیستم را تشکیل می دهد. علم اقتصاد تا به امروز در مرحله‌ای از توسعه خود قرار دارد که در آن روش‌ها و روش‌های جدید و در بسیاری موارد غیراستاندارد مدل‌سازی فیزیکی و ریاضی فرآیندهای اقتصادی به‌ویژه در آن به‌طور مؤثر مورد استفاده قرار می‌گیرد. اینجاست که نتیجه گیری در مورد لزوم ایجاد، مطالعه و ساخت مدل هایی که به نحوی بتواند وضعیت اقتصادی را توصیف کند، به دست می آید.

در مورد دلیل انتخاب تحلیل کیفی به جای تحلیل کمی، شایان ذکر است که در اکثریت قریب به اتفاق موارد، نتایج و نتایج حاصل از تجزیه و تحلیل کیفی سیستم‌های دینامیکی مهم‌تر از نتایج تحلیل کمی آن‌ها است. در چنین شرایطی جا دارد به اظهارات وی.پ. میلوانوف، که در آن بیان می کند که آنها به طور سنتی معتقدند که نتایج مورد انتظار هنگام اعمال روش های ریاضی برای تجزیه و تحلیل اشیاء واقعی باید به یک نتیجه عددی کاهش یابد. از این نظر، روش های کیفی کار تا حدودی متفاوتی دارند. بر دستیابی به نتیجه ای که کیفیت سیستم را توصیف می کند، بر جستجوی ویژگی های مشخصه همه پدیده ها به عنوان یک کل، بر پیش بینی تمرکز می کند. البته، درک چگونگی تغییر تقاضا هنگام تغییر قیمت برای نوع خاصی از کالا بسیار مهم است، اما فراموش نکنید که درک اینکه آیا در چنین شرایطی کمبود یا مازاد این کالاها وجود خواهد داشت بسیار مهم تر است (دیمیتریف ، 2016).

هدف این مطالعه دیفرانسیل غیرخطی و دینامیک سیستم است.

در این مورد موضوع تحقیق شرح فرآیند تعامل بین شرکت ها از طریق دیفرانسیل غیرخطی و دینامیک سیستم می باشد.

با صحبت در مورد کاربرد عملی مطالعه، ارزش آن را دارد که بلافاصله آن را به دو بخش تقسیم کنیم. یعنی تحلیل نظری یعنی تحلیل کیفی سیستم ها و عملی که در آن ساخت مدل های شبیه سازی در نظر گرفته می شود.

بخش نظری این پژوهش به ارائه مفاهیم و پدیده های اساسی می پردازد. سیستم‌های دیفرانسیل ساده را در نظر می‌گیرد، مانند کارهای بسیاری از نویسندگان دیگر (Tschl، 2012؛ Nolte، 2015)، اما در عین حال امکان توصیف تعامل بین شرکت‌ها را نیز فراهم می‌کند. بر این اساس، در آینده می توان مطالعات عمیق تری انجام داد، یا در غیر این صورت آشنایی خود را با آنچه که تجزیه و تحلیل کیفی سیستم ها را تشکیل می دهد، آغاز کرد.

از بخش عملی کار می توان برای ایجاد یک سیستم پشتیبانی تصمیم استفاده کرد. سیستم پشتیبانی تصمیم - یک سیستم اطلاعات خودکار با هدف حمایت از کسب و کار یا تصمیم گیری در یک سازمان، که به شما امکان می دهد بین گزینه های مختلف انتخاب کنید (Keen, 1980). حتی اگر مدل ها در حال حاضر خیلی دقیق نیستند، اما با تغییر آن ها برای یک شرکت خاص، می توانید به نتایج دقیق تری دست پیدا کنید. بنابراین، هنگام تغییر پارامترها و شرایط مختلفی که می تواند در بازار ایجاد شود، می توانید پیش بینی آینده را دریافت کنید و از قبل تصمیم سودآورتری بگیرید.

1. تعامل شرکت ها در شرایط متقابل

این مقاله سیستم‌های دو بعدی را ارائه می‌کند که در مقایسه با سیستم‌های درجه بالاتر بسیار ساده هستند، اما در عین حال به ما اجازه می‌دهند تا روابط بین سازمان‌هایی را که نیاز داریم نشان دهیم.

شروع کار با انتخاب نوع تعامل است که در آینده توضیح داده خواهد شد، زیرا برای هر یک از انواع سیستم هایی که آنها را توصیف می کنند، هرچند اندکی، متفاوت هستند. شکل 1.1 طبقه بندی Yujim Odum را برای تعامل جمعیت اصلاح شده برای تعامل اقتصادی نشان می دهد (Odum, 1968) که بر اساس آن ما تعامل شرکت ها را بیشتر در نظر خواهیم گرفت.

شکل 1.1. انواع تعامل بین شرکت ها

بر اساس شکل 1.1، ما 4 نوع تعامل را مشخص می کنیم و برای هر یک از آنها سیستمی از معادلات را ارائه می دهیم که آنها را بر اساس مدل مالتوس توصیف می کند (مالتوس، 1798). بر اساس آن، نرخ رشد متناسب با فراوانی فعلی گونه است، به عبارت دیگر، می توان آن را با معادله دیفرانسیل زیر توصیف کرد:

که در آن a پارامتری است که به رشد طبیعی جمعیت بستگی دارد. همچنین شایان ذکر است که در سیستم های در نظر گرفته شده در زیر، تمام پارامترها و همچنین متغیرها مقادیر غیر منفی می گیرند.

تولید مواد اولیه تولید محصولاتی است که مشابه مدل شکارچی-شکار است. مدل شکارچی-شکار، همچنین به عنوان مدل Lotka-Volterra شناخته می شود، یک جفت معادلات دیفرانسیل مرتبه اول غیر خطی است که دینامیک یک سیستم بیولوژیکی با دو گونه را توصیف می کند که یکی از آنها شکارچی و دیگری طعمه (Llibre) است. ، 2007). تغییر در فراوانی این گونه ها با سیستم معادلات زیر توصیف می شود:

(1.2)

که در آن - رشد تولید اولین شرکت را بدون تأثیر دومین شرکت مشخص می کند (در مورد مدل شکارچی-شکار، رشد جمعیت طعمه بدون شکارچیان)،

این رشد تولید شرکت دوم را بدون تأثیر اولین (رشد جمعیت شکارچیان بدون طعمه) مشخص می کند.

این رشد تولید اولین شرکت را با در نظر گرفتن تأثیر شرکت دوم بر روی آن مشخص می کند (افزایش تعداد طعمه هنگام تعامل با شکارچیان).

این رشد تولید شرکت دوم را با در نظر گرفتن تأثیر شرکت اول بر آن (افزایش تعداد شکارچیان در طول تعامل آنها با قربانیان) مشخص می کند.

برای یکی، شکارچی، همانطور که از سیستم، و همچنین طبقه بندی Odum مشاهده می شود، تعامل آنها تأثیر مطلوبی را تحمیل می کند. از سوی دیگر نامطلوب. اگر در واقعیت های اقتصادی در نظر گرفته شود، همانطور که در شکل مشاهده می شود، ساده ترین آنالوگ سازنده و تامین کننده منابع آن است که به ترتیب با شکارچی و طعمه مطابقت دارد. بنابراین، در غیاب مواد خام، تولید به طور تصاعدی کاهش می یابد.

رقابت رقابت بین دو یا چند گونه (در مورد ما سیستم های دو بعدی را در نظر می گیریم، بنابراین دقیقاً رقابت دو گونه را در نظر می گیریم) گونه ها، گروه های اقتصادی برای قلمروها، منابع محدود یا ارزش های دیگر است (التون، 1968). تغییرات در تعداد گونه ها، یا تعداد محصولات در مورد ما، توسط سیستم زیر توضیح داده شده است:

(1.3)

در این حالت، گونه ها یا شرکت هایی که یک محصول را تولید می کنند، بر یکدیگر تأثیر منفی می گذارند. یعنی در غیاب رقیب رشد محصول به صورت تصاعدی افزایش می یابد.

حالا بیایید به یک تعامل همزیستی برویم، که در آن هر دو شرکت تأثیر مثبتی بر یکدیگر دارند. بیایید با متقابل گرایی شروع کنیم. متقابل نوعی رابطه بین گونه های مختلف است که در آن هر یک از آنها از اعمال دیگری سود می برند و شایان ذکر است که وجود شریک شرط لازم وجود است (تامپسون، 2005). این نوع رابطه توسط سیستم توصیف می شود:

(1.4)

از آنجایی که تعامل بین شرکت ها برای وجود آنها ضروری است، در صورت عدم وجود محصول یک شرکت، خروجی کالاهای شرکت دیگر به طور تصاعدی کاهش می یابد. این زمانی امکان پذیر است که شرکت ها به سادگی جایگزین دیگری برای خرید نداشته باشند.

نوع دیگری از تعامل همزیستی، همکاری اولیه را در نظر بگیرید. همکاری اولیه مشابه متقابل گرایی است، با این استثنا که نیازی به وجود شریک نیست، زیرا برای مثال، جایگزین های دیگری وجود دارد. از آنجایی که آنها مشابه هستند، سیستم های آنها تقریباً یکسان به نظر می رسند:

(1.5)

بنابراین عدم وجود محصول یک شرکت مانع رشد محصول شرکت دیگر نمی شود.

البته، علاوه بر موارد ذکر شده در پاراگراف های 3 و 4، انواع دیگری از روابط همزیستی را می توان ذکر کرد: کامنسالیسم و ​​آمنسالیسم (هانسکی، 1999). اما از آنجایی که در کامنسالیسم یکی از شرکا نسبت به تعامل خود با دیگری بی تفاوت است، به آنها اشاره نمی شود، اما همچنان مواردی را در نظر می گیریم که نفوذ وجود دارد. و آمنسالیسم در نظر گرفته نمی شود، زیرا از نظر اقتصادی، چنین روابطی، وقتی تعامل آنها به یکی آسیب می زند و دیگری بی تفاوت باشد، به سادگی نمی تواند وجود داشته باشد.

با توجه به تأثیر شرکت‌ها بر یکدیگر، یعنی اینکه روابط همزیستی منجر به همزیستی پایدار شرکت‌ها می‌شود، در این مقاله تنها مواردی از هم‌گرایی و همکاری اولیه را بررسی می‌کنیم، زیرا در هر دو مورد تعامل برای همه مفید است.

این فصل به تعامل شرکت ها در شرایط متقابل اختصاص دارد. دو سیستم را در نظر می گیرد که توسعه بیشتر سیستم های مبتنی بر مدل مالتوس هستند، یعنی سیستم هایی با محدودیت های تحمیلی در افزایش تولید.

پویایی یک جفت متصل شده توسط روابط متقابل، همانطور که در بالا ذکر شد، در اولین تقریب توسط سیستم قابل توصیف است:

(1.6)

مشاهده می شود که با تولید اولیه زیاد، سیستم به طور نامحدود رشد می کند و با مقدار کم، تولید کاهش می یابد. اینجاست که نادرستی توصیف دوخطی تأثیر ناشی از دوسویه نهفته است. برای اینکه بخواهیم تصویر را تصحیح کنیم، عاملی شبیه به اشباع شکارچی معرفی می کنیم، یعنی عاملی که در صورت بیش از حد، نرخ رشد تولید را کاهش می دهد. در این صورت به سیستم زیر می رسیم:

(1.7)

رشد تولید محصول شرکت اول در تعامل با شرکت دوم با در نظر گرفتن اشباع کجاست؟

رشد تولید محصول شرکت دوم در تعامل با شرکت اول با در نظر گرفتن اشباع،

ضرایب اشباع

بنابراین، ما دو سیستم دریافت کردیم: مدل مالتوسی رشد با و بدون اشباع.

1.1 پایداری سیستم ها در تقریب اول

پایداری سیستم ها در تقریب اول در بسیاری از آثار خارجی (Hairer, 1993; Bhatia, 2002; Khalil, 2001; Strogatz, 2001 و دیگران) و روسی زبان (Akhromeyeva, 1992; Bellman, 1954; Demidovich, 1954, 1967; کراسوفسکی، 1959 و دیگران)، و تعریف آن یک گام اساسی برای تجزیه و تحلیل فرآیندهای رخ داده در سیستم است. برای این کار مراحل لازم زیر را انجام دهید:

بیایید نقاط تعادل را پیدا کنیم.

اجازه دهید ماتریس ژاکوبین سیستم را پیدا کنیم.

مقادیر ویژه ماتریس ژاکوبین را پیدا کنید.

ما نقاط تعادل را طبق قضیه لیاپانوف طبقه بندی می کنیم.

با در نظر گرفتن مراحل، بهتر است در توضیح بیشتر آنها صحبت کنیم، بنابراین تعاریفی را ارائه می کنم و روش هایی را که در هر یک از این مراحل استفاده خواهیم کرد، شرح می دهم.

گام اول، جستجوی نقاط تعادل است. برای یافتن آنها، هر تابع را با صفر برابر می کنیم. یعنی سیستم را حل می کنیم:

که در آن a و b به معنای تمام پارامترهای معادله است.

قدم بعدی یافتن ماتریس ژاکوبین است. در مورد ما، این یک ماتریس 2 در 2 با اولین مشتقات در نقطه ای خواهد بود، همانطور که در زیر نشان داده شده است:

پس از انجام دو مرحله اول، به ریشه‌یابی معادله مشخصه زیر می‌پردازیم:

جایی که نقطه مطابق با نقاط تعادلی است که در مرحله اول یافت شد.

پس از یافتن و، به مرحله چهارم می رویم و از قضایای لیاپانوف زیر استفاده می کنیم (پارکس، 1992):

قضیه 1: اگر همه ریشه های معادله مشخصه دارای قسمت واقعی منفی باشند، نقطه تعادل مربوط به سیستم های اصلی و خطی شده به طور مجانبی پایدار است.

قضیه 2: اگر حداقل یکی از ریشه های معادله مشخصه دارای قسمت واقعی مثبت باشد، نقطه تعادل مربوط به سیستم های اصلی و خطی شده به طور مجانبی ناپایدار است.

همچنین با توجه به تقسیم بندی نشان داده شده در شکل 1.2 (دانشگاه لامار) می توان نوع پایداری را با دقت بیشتری تعیین کرد.

شکل 1.2. انواع پایداری نقاط تعادل

با در نظر گرفتن اطلاعات نظری لازم، به تحلیل سیستم ها می پردازیم.

یک سیستم بدون اشباع را در نظر بگیرید:

این بسیار ساده است و برای استفاده عملی مناسب نیست، زیرا هیچ محدودیتی ندارد. اما به عنوان اولین نمونه از تجزیه و تحلیل سیستم برای بررسی مناسب است.

ابتدا اجازه دهید نقاط تعادل را با مساوی کردن سمت راست معادلات با صفر بیابیم. بنابراین، ما دو نقطه تعادل را پیدا می کنیم، آنها را A و B می نامیم: .

بیایید گام را با جستجوی ماتریس ژاکوبین، ریشه های معادله مشخصه و تعیین نوع پایداری ترکیب کنیم. از آنجایی که آنها ابتدایی هستند، بلافاصله پاسخ را دریافت می کنیم:

1. در نقطه , , یک گره پایدار وجود دارد.

در نقطه: . . زین اسب.

همانطور که قبلاً نوشتم، این سیستم بسیار بی اهمیت است، بنابراین نیازی به توضیح نیست.

حال بیایید سیستم را از اشباع آنالیز کنیم:

(1.9)

ظهور محدودیت در اشباع متقابل محصولات توسط شرکت ها ما را به تصویر واقعی آنچه در حال وقوع است نزدیک می کند و همچنین سیستم را کمی پیچیده می کند.

مانند قبل، قسمت های مناسب سیستم را با صفر برابر می کنیم و سیستم حاصل را حل می کنیم. نقطه بدون تغییر باقی مانده است، اما نقطه دیگر در این مورد شامل پارامترهای بیشتری نسبت به قبل است: .

در این مورد، ماتریس ژاکوبی به شکل زیر است:

ماتریس هویت ضرب شده در آن را از آن کم کنید و تعیین کننده ماتریس حاصل را در نقاط A و B با صفر برابر کنید.

در نقطه ای از تصویر اولیه مشابه:

گره پایدار

اما در نقطه همه چیز تا حدودی پیچیده تر است، و اگرچه ریاضیات هنوز بسیار ساده است، پیچیدگی باعث ناراحتی کار با عبارات تحت اللفظی طولانی می شود. از آنجایی که مقادیر بسیار طولانی و ناخوشایند نوشته شده اند، داده نمی شوند، کافی است بگوییم که در این مورد، مانند سیستم قبلی، نوع پایداری به دست آمده یک زین است.

2 پرتره فازی از سیستم ها

اکثریت قریب به اتفاق مدل های دینامیکی غیرخطی معادلات دیفرانسیل پیچیده ای هستند که یا قابل حل نیستند یا این نوعی پیچیدگی است. یک مثال سیستم مربوط به بخش قبل است. علیرغم سادگی ظاهری، یافتن نوع پایداری در نقطه تعادل دوم کار آسانی نبود (البته نه از نظر ریاضی) و با افزایش پارامترها، محدودیت ها و معادلات برای افزایش تعداد شرکت های در حال تعامل، پیچیدگی فقط افزایش خواهد یافت. البته، اگر پارامترها عبارات عددی باشند، همه چیز به طرز باورنکردنی ساده می شود، اما پس از آن تجزیه و تحلیل به نوعی معنای خود را از دست می دهد، زیرا در نهایت، ما قادر خواهیم بود نقاط تعادلی را پیدا کنیم و انواع پایداری آنها را فقط برای یک خاص مشخص کنیم. مورد، یک مورد عمومی نیست.

در چنین مواردی، ارزش به یاد آوردن صفحه فاز و پرتره های فاز را دارد. در ریاضیات کاربردی، به‌ویژه زمینه تحلیل سیستم‌های غیرخطی، صفحه فاز نمایشی بصری از ویژگی‌های معینی از انواع معینی از معادلات دیفرانسیل است (نولت، 2015). صفحه مختصات با محورهای مقادیر هر جفت متغیری که وضعیت سیستم را مشخص می کند یک حالت دو بعدی از یک فضای فاز مشترک n بعدی است.

به لطف صفحه فاز، می توان به صورت گرافیکی وجود چرخه های حد را در راه حل های یک معادله دیفرانسیل تعیین کرد.

جواب های یک معادله دیفرانسیل خانواده ای از توابع هستند. از نظر گرافیکی، این می تواند در صفحه فاز به عنوان یک میدان برداری دو بعدی ترسیم شود. بردارها بر روی صفحه ترسیم می شوند، که مشتقات را در نقاط مشخص با توجه به برخی پارامترها نشان می دهند، در مورد ما، با توجه به زمان، یعنی (). با تعداد کافی از این فلش ها در یک منطقه، رفتار سیستم را می توان تجسم کرد و چرخه های حد را می توان به راحتی شناسایی کرد (بوئینگ، 2016).

میدان برداری یک پرتره فاز است، یک مسیر خاص در امتداد خط جریان (یعنی یک مسیر همیشه مماس بر بردارها) یک مسیر فاز است. جریان در یک میدان برداری نشان دهنده تغییر در سیستم در طول زمان است که توسط یک معادله دیفرانسیل توصیف شده است (جردن، 2007).

شایان ذکر است که حتی بدون حل معادله دیفرانسیل نیز می توان یک پرتره فاز ساخت و در عین حال، تجسم خوب می تواند اطلاعات مفید زیادی را ارائه دهد. علاوه بر این، در حال حاضر برنامه های زیادی وجود دارد که می تواند به ساخت نمودارهای فاز کمک کند.

بنابراین، صفحات فاز برای تجسم رفتار سیستم های فیزیکی مفید هستند. به طور خاص، سیستم های نوسانی، مانند مدل شکارچی-شکار که قبلاً در بالا ذکر شد. در این مدل‌ها، مسیرهای فاز می‌توانند به سمت صفر بپیچند، از یک مارپیچ تا بی نهایت خارج شوند یا به یک وضعیت پایدار خنثی به نام مراکز برسند. این برای تعیین پایداری یا عدم ثبات دینامیک مفید است (جردن، 2007).

پرتره های فاز ارائه شده در این بخش با استفاده از ابزار WolframAlpha ساخته می شوند یا از منابع دیگر ارائه می شوند. مدل رشد مالتوسی بدون اشباع

اجازه دهید یک پرتره فازی از اولین سیستم با سه مجموعه پارامتر بسازیم تا رفتار آنها را مقایسه کنیم. مجموعه A ((1،1)، (1،1))، که به عنوان یک مجموعه واحد، مجموعه B ((10،0.1)، (2،2)) نامیده می شود، هنگامی که انتخاب می شود، سیستم یک تیز را تجربه می کند. کاهش تولید، و مجموعه C ((1،10)، (1،10)) که برعکس، رشد شدید و نامحدودی برای آن رخ می دهد. لازم به ذکر است که مقادیر در امتداد محورها در همه موارد در فواصل یکسانی از 10- تا 10 خواهد بود تا به راحتی بتوان نمودارهای فاز را با یکدیگر مقایسه کرد. البته این در مورد پرتره کیفی سیستم که محورهای آن بی بعد هستند صدق نمی کند.

شکل 1.3 پرتره فاز با پارامترهای A

معادله حد دیفرانسیل متقابل

شکل 1.3 بالا پرتره های فاز سیستم را برای سه مجموعه پارامتر مشخص شده و همچنین پرتره فاز توصیف کننده رفتار کیفی سیستم نشان می دهد. فراموش نکنید که از نظر عملی مهمترین آن سه ماهه اول است، زیرا میزان تولید که فقط می تواند غیرمنفی باشد، محورهای ماست.

در هر یک از شکل ها، ثبات در نقطه تعادل (0,0) به وضوح قابل مشاهده است. و در شکل اول، "نقطه زین" نیز در نقطه (1،1) قابل توجه است، به عبارت دیگر، اگر مقادیر مجموعه پارامترها را در سیستم جایگزین کنیم، سپس در نقطه تعادل B. هنگامی که مرزهای ساختمان مدل تغییر می کند، نقطه زین در سایر پرتره های فاز نیز یافت می شود.

مدل مالتوسی رشد از اشباع.

اجازه دهید نمودارهای فازی را برای سیستم دوم، که در آن اشباع وجود دارد، با سه مجموعه جدید از مقادیر پارامتر بسازیم. مجموعه A، ((0.1،15،100)، (0.1،15،100))، مجموعه B ((1،1،0.5)، (1، 1،0.5)) و مجموعه C ((20،1،100)، (20،1،100) )).

شکل 1.4. پرتره فاز با پارامترهای A

همانطور که می بینید، برای هر مجموعه ای از پارامترها، نقطه (0,0) تعادل و همچنین پایدار است. همچنین در برخی از شکل ها یک نقطه زین را مشاهده می کنید.

در این مورد، مقیاس های مختلفی در نظر گرفته شد تا به وضوح نشان دهد که حتی زمانی که یک عامل اشباع به سیستم اضافه می شود، تصویر کیفی تغییر نمی کند، یعنی اشباع به تنهایی کافی نیست. باید در نظر داشت که در عمل شرکت ها به ثبات نیاز دارند، یعنی اگر معادلات دیفرانسیل غیرخطی را در نظر بگیریم، بیشتر به نقاط تعادل پایدار علاقه مندیم و در این سیستم ها فقط نقاط صفر چنین نقاطی هستند. که چنین مدل های ریاضی به وضوح برای شرکت ها مناسب نیستند. به هر حال، این بدان معناست که تنها با تولید صفر، شرکت ها در ثبات هستند که به وضوح با تصویر واقعی جهان متفاوت است.

در ریاضیات، منحنی انتگرال یک منحنی پارامتری است که یک راه حل خاص برای یک معادله دیفرانسیل معمولی یا سیستم معادلات را نشان می دهد (لنگ، 1972). اگر معادله دیفرانسیل به صورت یک میدان برداری نمایش داده شود، منحنی های انتگرال مربوطه در هر نقطه بر میدان مماس هستند.

بسته به ماهیت و تفسیر معادله دیفرانسیل یا میدان برداری، منحنی های انتگرال با نام های دیگری نیز شناخته می شوند. در فیزیک، منحنی های انتگرال برای میدان الکتریکی یا میدان مغناطیسی به عنوان خطوط میدان شناخته می شوند و منحنی های انتگرال برای یک میدان سرعت سیال به عنوان خطوط جریان شناخته می شوند. در سیستم های دینامیکی، منحنی های انتگرال برای یک معادله دیفرانسیل، مسیر نامیده می شوند.

شکل 1.5. منحنی های انتگرال

راه حل های هر یک از سیستم ها را می توان معادلات منحنی های انتگرال نیز در نظر گرفت. بدیهی است که هر مسیر فاز، طرحی از منحنی انتگرال در فضای x,y,t بر روی صفحه فاز است.

روش های مختلفی برای ساخت منحنی های انتگرال وجود دارد.

یکی از آنها روش ایزوکلاین است. ایزوکلاین منحنی است که از نقاطی می گذرد که در آن شیب تابع مورد نظر بدون توجه به شرایط اولیه همیشه یکسان خواهد بود (Hanski, 1999).

اغلب به عنوان یک روش گرافیکی برای حل معادلات دیفرانسیل معمولی استفاده می شود. به عنوان مثال، در معادله ای به شکل y "= f (x, y)، خطوط همسو خطوطی هستند در صفحه (x, y) که از معادل سازی f (x, y) به یک ثابت به دست می آیند. این یک سری از خطوط ( برای ثابت های مختلف) که در امتداد آنها راه حل های منحنی شیب یکسانی دارند. با محاسبه این گرادیان برای هر ایزوکلاین، می توان میدان شیب را مشاهده کرد و رسم منحنی های حل تقریبی را نسبتاً آسان می کند. شکل زیر نمونه ای از استفاده از روش ایزوکلاین را نشان می دهد. .

شکل 1.6. روش ایزوکلاین

این روش نیازی به محاسبات کامپیوتری ندارد و در گذشته بسیار رایج بود. اکنون راه‌حل‌های نرم‌افزاری وجود دارد که منحنی‌های یکپارچه را روی رایانه‌ها با دقت و سرعت بسیار بالا ایجاد می‌کنند. با این حال، با این حال، روش ایزوکلاین به خوبی خود را به عنوان ابزاری برای مطالعه رفتار راه حل ها نشان داده است، زیرا به فرد اجازه می دهد مناطق رفتار معمولی منحنی های انتگرال را نشان دهد.

مدل رشد مالتوسی بدون اشباع

بیایید با این واقعیت شروع کنیم که با وجود روش های مختلف ساخت، نشان دادن منحنی های انتگرال یک سیستم معادلات چندان آسان نیست. روش ایزوکلاین که قبلا ذکر شد مناسب نیست زیرا برای معادلات دیفرانسیل مرتبه اول کار می کند. و ابزارهای نرم افزاری که توانایی ترسیم چنین منحنی هایی را دارند در دسترس عموم نیستند. به عنوان مثال Wolfram Mathematica که توانایی این را دارد، پرداخت می شود. بنابراین سعی خواهیم کرد تا حد امکان از قابلیت های Wolfram Alpha که در مقالات و آثار مختلف شرح کار با آن آمده است استفاده کنیم (Orca, 2009). حتی با وجود این واقعیت که تصویر کاملاً قابل اعتماد نخواهد بود، اما حداقل به شما امکان می دهد وابستگی را در هواپیماها (x، t)، (y، t) نشان دهید. ابتدا اجازه دهید هر یک از معادلات t را حل کنیم. یعنی وابستگی هر یک از متغیرها را نسبت به زمان استخراج می کنیم. برای این سیستم دریافت می کنیم:

(1.10)

(1.11)

معادلات متقارن هستند، بنابراین ما فقط یکی از آنها را در نظر می گیریم، یعنی x(t). اجازه دهید ثابت برابر با 1 باشد. در این حالت از تابع رسم استفاده خواهیم کرد.

شکل 1.7. مدل سه بعدی برای معادله (1.10)

مدل مالتوسی رشد از اشباع.

بیایید همین کار را برای مدل دیگر انجام دهیم. در نهایت دو معادله بدست می آوریم که وابستگی متغیرها به زمان را نشان می دهد.

(1.12)

(1.13)

بیایید دوباره یک مدل سه بعدی و خطوط تراز بسازیم.

شکل 1.8. مدل سه بعدی برای معادله (1.12)

از آنجایی که مقادیر متغیرها غیر منفی هستند، در کسری با توان یک عدد منفی به دست می آوریم. بنابراین، منحنی انتگرال با زمان کاهش می یابد.

قبلاً برای درک اصل کار تعریفی از دینامیک سیستم ارائه شده بود، اما اکنون اجازه دهید با جزئیات بیشتر در مورد آن صحبت کنیم.

دینامیک سیستم یک روش و روش مدل‌سازی ریاضی برای شکل‌گیری، درک و بحث درباره مسائل پیچیده است که در ابتدا در دهه 1950 توسط جی فورستر توسعه یافت و در کار خود توضیح داده شد (فورستر، 1961).

دینامیک سیستم یکی از جنبه های نظریه سیستم ها به عنوان روشی برای درک رفتار دینامیکی سیستم های پیچیده است. اساس این روش تشخیص این است که ساختار هر سیستم از روابط متعددی بین اجزای آن تشکیل شده است که اغلب به اندازه خود اجزای منفرد در تعیین رفتار آن مهم هستند. به عنوان مثال می توان به نظریه آشوب و پویایی اجتماعی اشاره کرد که در آثار نویسندگان مختلف شرح داده شده است (گربوگی، 1987؛ سونتاگ، 1998؛ کوزنتسوف، 2001؛ تابور، 2001). همچنین استدلال می شود که از آنجایی که خصوصیات کل را اغلب نمی توان در ویژگی های عنصر یافت، در برخی موارد رفتار کل را نمی توان بر حسب رفتار اجزا توضیح داد.

شبیه سازی واقعاً می تواند اهمیت عملی کامل یک سیستم پویا را نشان دهد. اگرچه در صفحات گسترده امکان پذیر است، اما بسته های نرم افزاری زیادی وجود دارند که به طور خاص برای این منظور بهینه شده اند.

مدل سازی خود فرآیند ایجاد و تجزیه و تحلیل یک نمونه اولیه از یک مدل فیزیکی به منظور پیش بینی عملکرد آن در دنیای واقعی است. از مدل سازی شبیه سازی برای کمک به طراحان و مهندسان استفاده می شود تا درک کنند که در چه شرایطی و در چه مواردی یک فرآیند می تواند شکست بخورد و چه بارهایی را می تواند تحمل کند (Khemdy, 2007). مدل سازی همچنین می تواند به پیش بینی رفتار جریان سیال و سایر پدیده های فیزیکی کمک کند. این مدل شرایط کاری تقریبی را با توجه به نرم‌افزار شبیه‌سازی کاربردی تحلیل می‌کند (Strogalev، 2008).

محدودیت در امکانات مدل سازی شبیه سازی یک دلیل مشترک دارد. ساخت و محاسبه عددی یک مدل دقیق تنها در مناطقی موفقیت را تضمین می کند که یک نظریه کمی دقیق وجود داشته باشد، یعنی زمانی که معادلات توصیف کننده پدیده های خاص شناخته شده باشند، و وظیفه تنها حل این معادلات با دقت لازم است. در مناطقی که نظریه کمی وجود ندارد، ساخت یک مدل دقیق ارزش محدودی دارد (بازیکین، 2003).

با این حال، امکانات مدل سازی نامحدود نیست. اول از همه، این به دلیل این واقعیت است که ارزیابی دامنه کاربرد مدل شبیه‌سازی، به‌ویژه، دوره زمانی که می‌توان پیش‌بینی را با دقت مورد نیاز ساخت، دشوار است (Law, 2006). علاوه بر این، به دلیل ماهیت خود، مدل شبیه‌سازی به یک شی خاص گره خورده است، و هنگام تلاش برای اعمال آن بر روی یک شی دیگر، حتی مشابه، نیاز به یک تنظیم اساسی یا حداقل یک تغییر قابل توجه دارد.

یک دلیل کلی برای وجود محدودیت در شبیه سازی وجود دارد. ساخت و محاسبه عددی یک مدل «دقیق» تنها در صورتی موفق است که یک نظریه کمی وجود داشته باشد، یعنی تنها در صورتی که همه معادلات شناخته شده باشند، و مشکل تنها به حل این معادلات با دقت خاصی کاهش یابد (بازیکین، 2003).

اما حتی با وجود این، مدل‌سازی شبیه‌سازی یک ابزار عالی برای تجسم فرآیندهای پویا است که با یک مدل کم و بیش صحیح، امکان تصمیم‌گیری بر اساس نتایج آن را فراهم می‌کند.

در این کار، مدل‌های سیستم با استفاده از ابزار دینامیک سیستم ارائه شده توسط برنامه AnyLogic ساخته خواهند شد.

مدل رشد مالتوسی بدون اشباع/

قبل از ساخت یک مدل، لازم است عناصر دینامیک سیستم را که از آنها استفاده خواهیم کرد در نظر بگیریم و آنها را با سیستم خود مرتبط کنیم. تعاریف زیر از اطلاعات راهنمای برنامه AnyLogic گرفته شده است.

درایو عنصر اصلی نمودارهای دینامیک سیستم است. آنها برای نشان دادن اشیاء دنیای واقعی استفاده می شوند که در آن منابع خاصی انباشته می شوند: پول، مواد، تعداد گروه های مردم، برخی از اشیاء مادی و غیره. انباشته کننده ها حالت استاتیک سیستم شبیه سازی شده را منعکس می کنند و مقادیر آنها در طول زمان مطابق با جریان های موجود در سیستم تغییر می کند. نتیجه این است که دینامیک سیستم توسط جریان ها تعیین می شود. جریان های ورودی و خروجی از آکومولاتور باعث افزایش یا کاهش مقادیر آکومولاتور می شود.

جریان، و همچنین درایو فوق، عنصر اصلی نمودارهای دینامیک سیستم است.

در حالی که سطل‌ها قسمت استاتیک سیستم را تعریف می‌کنند، جریان‌ها میزان تغییر سطل‌ها را تعیین می‌کنند، یعنی نحوه تغییر ذخایر در طول زمان، و در نتیجه پویایی سیستم را تعیین می‌کنند.

عامل ممکن است دارای متغیرهایی باشد. متغیرها معمولاً برای مدل‌سازی ویژگی‌های متغیر یک عامل یا ذخیره نتایج مدل استفاده می‌شوند. به طور معمول، متغیرهای پویا از توابع انباشته تشکیل شده اند.

عامل ممکن است پارامترهایی داشته باشد. پارامترها اغلب برای نشان دادن برخی از ویژگی های شی مدل شده استفاده می شوند. آنها زمانی مفید هستند که نمونه های شی همان رفتاری را داشته باشند که در کلاس توضیح داده شد، اما در برخی مقادیر پارامتر متفاوت باشند. تفاوت واضحی بین متغیرها و پارامترها وجود دارد. متغیر نشان دهنده وضعیت مدل است و می تواند در طول شبیه سازی تغییر کند. این پارامتر معمولاً برای توصیف اشیا به صورت ایستا استفاده می شود. در طول یک «اجرای» مدل، پارامتر معمولاً یک ثابت است و تنها زمانی تغییر می‌کند که رفتار مدل نیاز به پیکربندی مجدد داشته باشد.

پیوند عنصری از پویایی سیستم است که برای تعیین رابطه بین عناصر یک نمودار جریان و انباشته‌کننده‌ها استفاده می‌شود. به طور خودکار پیوندهایی ایجاد نمی‌کند، اما کاربر را مجبور می‌کند که به صراحت آنها را در ویرایشگر گرافیکی ترسیم کند (البته شایان ذکر است. که AnyLogic همچنین از مکانیزمی برای تنظیم سریع لینک های از دست رفته پشتیبانی می کند). به عنوان مثال، اگر هر عنصر A در معادله یا مقدار اولیه عنصر B ذکر شده باشد، ابتدا باید این عناصر را با پیوندی که از A به B می رود به هم متصل کنید و تنها سپس عبارت را در ویژگی های B وارد کنید. .

برخی عناصر دیگر از پویایی سیستم وجود دارد، اما آنها در روند کار دخالتی ندارند، بنابراین آنها را حذف می کنیم.

برای شروع، اجازه دهید در نظر بگیریم که مدل سیستم (1.4) از چه چیزی تشکیل خواهد شد.

ابتدا بلافاصله دو درایو را علامت گذاری می کنیم که حاوی مقادیر مقدار تولید هر یک از شرکت ها است.

ثانیاً، از آنجایی که در هر معادله دو جمله داریم، به هر یک از درایوها دو جریان دریافت می کنیم، یکی ورودی و دیگری خروجی.

ثالثاً به متغیرها و پارامترها منتقل می کنیم. فقط دو متغیر وجود دارد. X و Y مسئول رشد تولید هستند. ما هم چهار گزینه داریم.

چهارم، در رابطه با اتصالات، هر یک از جریان ها باید با متغیرها و پارامترهای موجود در معادله جریان همراه باشد و هر دو متغیر باید با انباشته کننده ها همراه باشند تا مقدار در طول زمان تغییر کند.

ما شرح مفصلی از ساخت یک مدل را به عنوان نمونه ای از کار در محیط مدل سازی AnyLogic، برای سیستم بعدی می گذاریم، زیرا تا حدودی پیچیده تر است و از پارامترهای بیشتری استفاده می کند، و بلافاصله به بررسی نسخه نهایی آن می پردازیم. سیستم.

شکل 1.9 زیر مدل ساخته شده را نشان می دهد:

شکل 1.9. مدل دینامیک سیستم برای سیستم (1.4)

تمام عناصر دینامیک سیستم با مواردی که در بالا توضیح داده شد مطابقت دارند، به عنوان مثال. دو درایو، چهار جریان (دو ورودی، دو خروجی)، چهار پارامتر، دو متغیر پویا و پیوندهای ضروری.

شکل نشان می دهد که هر چه محصولات بیشتر باشد، رشد آن قوی تر است، که منجر به افزایش شدید تعداد کالاها می شود که با سیستم ما مطابقت دارد. اما همانطور که قبلا ذکر شد، عدم وجود محدودیت در این رشد، امکان اعمال این مدل را در عمل نمی دهد.

مدل رشد مالتوس از اشباع/

با توجه به این سیستم، اجازه دهید در مورد ساخت مدل با جزئیات بیشتر صحبت کنیم.

اولین مرحله اضافه کردن دو درایو است که آنها را X_stock و Y_stock می نامیم. بیایید یک مقدار اولیه برابر با 1 به هر یک از آنها اختصاص دهیم. توجه داشته باشید که در صورت عدم وجود جریان، چیزی در معادله ذخیره سازی کلاسیک وجود ندارد.

شکل 1.10. ساخت مدل سیستم (1.9)

مرحله بعدی اضافه کردن موضوعات است. بیایید یک جریان ورودی و خروجی برای هر درایو با استفاده از یک ویرایشگر گرافیکی بسازیم. ما نباید فراموش کنیم که یکی از لبه های جریان باید در درایو باشد، در غیر این صورت، آنها متصل نمی شوند.

می بینید که معادله درایو به طور خودکار تنظیم شده است، البته کاربر می تواند با انتخاب حالت معادله "سرطانی" آن را بنویسد، اما ساده ترین راه این است که این عمل را به برنامه بسپارید.

مرحله سوم ما اضافه کردن شش پارامتر و دو متغیر پویا است. بیایید به هر عنصر نامی مطابق با عبارت تحت اللفظی آن در سیستم بدهیم و همچنین مقادیر اولیه پارامترها را به صورت زیر تنظیم کنیم: e1=e2=1، a12=a21=3، n1=n2=0.2.

همه عناصر معادلات موجود هستند، فقط نوشتن معادلات برای جریان ها باقی می ماند، اما برای این کار ابتدا باید اتصالات بین عناصر را اضافه کنید. به عنوان مثال، جریان خروجی مسئول عبارت باید با e1 و x مرتبط باشد. و هر متغیر پویا باید با سهام مربوطه خود (X_stock x، Y_stock y) مرتبط باشد. ایجاد لینک شبیه به اضافه کردن موضوعات است.

پس از ایجاد اتصالات لازم می توانید به نوشتن معادلات برای جریان ها اقدام کنید که در شکل سمت راست نشان داده شده است. البته می توانید به ترتیب معکوس بروید، اما در صورت وجود اتصالات، هنگام نوشتن معادلات، نکاتی برای جایگزینی پارامترها / متغیرهای لازم ظاهر می شود که کار را در مدل های پیچیده آسان تر می کند.

پس از انجام تمامی مراحل می توانید مدل شبیه سازی را اجرا کرده و نتیجه آن را مشاهده کنید.

با در نظر گرفتن سیستم های معادلات دیفرانسیل غیرخطی برای تعامل شرکت ها در شرایط متقابل، می توان چندین نتیجه گرفت.

دو حالت سیستم وجود دارد: رشد نامحدود شدید، یا تمایل کمیت تولید به صفر. اینکه سیستم کدام یک از دو حالت را در نظر بگیرد به پارامترها بستگی دارد.

هیچ یک از مدل های پیشنهادی، از جمله مدل با در نظر گرفتن اشباع، برای استفاده عملی مناسب نیست، به دلیل عدم وجود موقعیت پایدار غیر صفر و همچنین دلایل شرح داده شده در بند 1.

در صورت تلاش برای مطالعه بیشتر این نوع تعامل همزیستی به منظور ایجاد مدلی قابل اجرا توسط شرکت ها در عمل، پیچیده تر کردن سیستم و معرفی پارامترهای جدید ضروری است. به عنوان مثال، بازیکین در کتاب خود مثالی از پویایی دو جمعیت متقابل را با معرفی یک عامل اضافی رقابت درون گونه ای ارائه می دهد. به همین دلیل سیستم به شکل زیر در می آید:

(1.15)

و در این حالت، یک موقعیت پایدار غیر صفر از سیستم ظاهر می شود که با یک "زین" از صفر جدا شده است، که آن را به تصویر واقعی آنچه در حال وقوع است نزدیک می کند.

2. تعامل شرکت ها در شرایط همکاری اولیه

تمام اطلاعات نظری اولیه در فصل قبل ارائه شد، بنابراین در تجزیه و تحلیل مدل های در نظر گرفته شده در این فصل، در اکثر موارد، نظریه حذف خواهد شد، به استثنای چند نکته که در قبل با آن مواجه نشدیم. فصل، و همچنین ممکن است کاهشی در محاسبات وجود داشته باشد. مدل تعامل بین سازمان ها در این فصل در شرایط همکاری اولیه که از سیستم های دو معادله بر اساس مدل مالتوسی تشکیل شده است، شبیه سیستم (1.5) است. سیستم های تحلیل شده در فصل قبل نشان داد که برای تقریب حداکثری آنها با مدل های موجود، لازم است سیستم ها پیچیده شوند. بر اساس این یافته ها، بلافاصله یک محدودیت رشد به مدل اضافه می کنیم. بر خلاف نوع قبلی تعامل، زمانی که رشدی که به شرکت دیگری وابسته نیست منفی است، در این حالت همه علائم مثبت است، یعنی رشد ثابتی داریم. با اجتناب از کاستی‌هایی که قبلاً توضیح داده شد، سعی می‌کنیم آن را به معادله لجستیک محدود کنیم که به معادله ورهولست نیز معروف است (گرشنفلد، 1999)، که به شکل زیر است:

, (2.1)

که در آن P اندازه جمعیت است، r پارامتری است که نرخ رشد را نشان می دهد، K پارامتری است که حداکثر اندازه جمعیت ممکن را بر عهده دارد. یعنی با گذشت زمان، اندازه جمعیت (در مورد ما تولید) به یک پارامتر خاص K گرایش پیدا می کند.

این معادله به مهار رشد تولید افسارگسیخته ای که تاکنون دیده ایم کمک خواهد کرد. بنابراین، سیستم به شکل زیر است:

(2.2)

فراموش نکنید که حجم کالاهای ذخیره شده در انبار برای هر شرکت متفاوت است، بنابراین پارامترهای محدود کننده رشد متفاوت است. بیایید این سیستم را "" بنامیم، و در آینده زمانی که آن را در نظر بگیریم از این نام استفاده خواهیم کرد.

سیستم دومی که در نظر خواهیم گرفت، توسعه بیشتر مدل با محدودیت Verhulst است. همانطور که در فصل قبل، یک محدودیت اشباع را معرفی می کنیم، سپس سیستم به شکل زیر در می آید:

(2.3)

اکنون هر یک از اصطلاحات حد خود را دارند، بنابراین بدون تجزیه و تحلیل بیشتر می توان دریافت که رشد نامحدودی مانند مدل های فصل قبل وجود نخواهد داشت. و از آنجایی که هر یک از اصطلاحات رشد مثبت را نشان می دهد، پس مقدار تولید به صفر نمی رسد. بیایید این مدل را «مدل عملیات اولیه دو محدود» بنامیم.

این دو مدل در منابع مختلف در مورد جمعیت های بیولوژیکی مورد بحث قرار گرفته اند. اکنون سعی خواهیم کرد تا حدودی سیستم ها را گسترش دهیم. برای این کار شکل زیر را در نظر بگیرید.

شکل نمونه ای از فرآیندهای دو شرکت صنایع فولاد و زغال سنگ را نشان می دهد. در هر دو بنگاه افزایش تولید مستقل از دیگری و همچنین افزایش تولید وجود دارد که به دلیل تعامل آنها حاصل می شود. ما قبلاً در مدل های قبلی این موضوع را در نظر گرفته ایم. اکنون شایان توجه است که شرکت ها نه تنها محصولاتی را تولید می کنند، بلکه آنها را به عنوان مثال به بازار یا شرکتی که با آن تعامل دارد، می فروشند. آن ها بر اساس نتیجه گیری های منطقی، نیاز به رشد منفی شرکت ها به دلیل فروش محصولات (در شکل، پارامترهای β1 و β2 مسئول این امر هستند) و همچنین به دلیل انتقال بخشی از محصولات به شرکت دیگری وجود دارد. . قبلاً این را فقط با علامت مثبت برای شرکت دیگری در نظر می گرفتیم، اما در هنگام انتقال محصولات به این واقعیت توجه نکردیم که تعداد محصولات برای اولین شرکت کاهش می یابد. در این حالت، سیستم را دریافت می کنیم:

(2.4)

و اگر بتوان در مورد این اصطلاح گفت که اگر در مدل های قبلی مشخص شده بود که افزایش طبیعی را مشخص می کند و پارامتر می تواند منفی باشد، عملاً هیچ تفاوتی وجود ندارد، پس در مورد اصطلاح این را نمی توان گفت علاوه بر این، در آینده، زمانی که چنین سیستمی را با محدودیتی در نظر می گیریم، استفاده از شرایط رشد مثبت و منفی صحیح تر است، زیرا در این صورت ممکن است محدودیت های مختلفی برای آنها اعمال شود که برای طبیعی غیر ممکن است. رشد بیایید آن را "مدل همکاری اولیه توسعه یافته" بنامیم.

در نهایت، مدل چهارم مورد بررسی، مدل همکاری اولیه توسعه یافته با محدودیت رشد لجستیکی است که قبلا ذکر شد. و سیستم این مدل به صورت زیر است:

, (2.5)

افزایش تولید اولین شرکت مستقل از دومی با در نظر گرفتن محدودیت لجستیکی کجاست؟ - افزایش تولید شرکت اول، بسته به شرکت دوم، با در نظر گرفتن محدودیت لجستیکی، - افزایش تولید شرکت دوم، مستقل از شرکت اول، با در نظر گرفتن محدودیت لجستیکی، - افزایش تولید شرکت دوم بسته به شرکت اول با در نظر گرفتن محدودیت لجستیکی - مصرف کالای شرکت اول غیرمرتبط با دیگری - مصرف کالای شرکت دوم غیر مرتبط با شرکت دیگر. ، - مصرف کالاهای صنعت اول توسط صنعت دوم ، - مصرف کالاهای صنعت دوم صنعت اول.

در آینده از این مدل به عنوان «مدل عملیاتی توسعه یافته با محدودیت لجستیکی» یاد می شود.

1 پایداری سیستم ها در تقریب اول

مدل عملیات اولیه با محدودیت Verhulst

روش‌هایی برای تجزیه و تحلیل پایداری سیستم در بخش مشابهی از فصل قبل نشان داده شد. اول از همه، ما نقاط تعادل را پیدا می کنیم. یکی از آنها مثل همیشه صفر است. دیگری نقطه ای با مختصات است.

برای نقطه صفر λ1 =، λ2 =، از آنجایی که هر دو پارامتر غیر منفی هستند، یک گره ناپایدار به دست می آوریم.

از آنجایی که کار با نقطه دوم چندان راحت نیست، به دلیل عدم توانایی کوتاه کردن عبارت، تعریف نوع پایداری را به نمودارهای فاز واگذار می کنیم، زیرا آنها به وضوح نشان می دهند که آیا نقطه تعادل پایدار است یا خیر. یا نه.

تحلیل این سیستم به دلیل اضافه شدن ضریب اشباع پیچیده‌تر از سیستم قبلی است، بنابراین پارامترهای جدیدی ظاهر می‌شوند و در هنگام یافتن نقاط تعادل، نیاز به حل یک معادله خطی نیست، بلکه یک معادله دوخطی است. متغیر در مخرج بنابراین، مانند مورد قبل، تعریف نوع پایداری را به نمودارهای فازی واگذار می کنیم.

علیرغم ظاهر شدن پارامترهای جدید، ژاکوبین در نقطه صفر و همچنین ریشه های معادله مشخصه، مشابه مدل قبلی به نظر می رسد. بنابراین، در نقطه صفر، یک گره ناپایدار.

بیایید به سراغ مدل های پیشرفته برویم. اولین مورد هیچ محدودیتی ندارد و به شکل سیستم (2.4) است.

بیایید تغییری در متغیرها ایجاد کنیم، , و . سیستم جدید:

(2.6)

در این حالت، دو نقطه تعادل، نقطه A(0,0)، B() بدست می آوریم. نقطه B در سه ماهه اول قرار دارد زیرا متغیرها دارای مقدار غیر منفی هستند.

برای نقطه تعادل A بدست می آوریم:

. - گره ناپایدار

. - زین اسب،

. - زین اسب،

. - گره پایدار

در نقطه B، ریشه های معادله مشخصه اعداد مختلط هستند: λ1 = , λ2 = . ما نمی‌توانیم با تکیه بر قضایای لیاپانوف نوع پایداری را تعیین کنیم، بنابراین شبیه‌سازی‌های عددی را انجام خواهیم داد که همه حالت‌های ممکن را نشان نمی‌دهند، اما به ما امکان می‌دهند حداقل برخی از آنها را پیدا کنیم.

شکل 2.2. شبیه سازی عددی جستجو برای نوع پایداری

با در نظر گرفتن این مدل، از آنجایی که دارای تعداد زیادی پارامتر مختلف و همچنین دو محدودیت است، باید با مشکلات محاسباتی روبرو شوید.

بدون وارد شدن به جزئیات محاسبات، به نقاط تعادل زیر می رسیم. نقطه A(0,0) و نقطه B با مختصات زیر:

()، جایی که a =

برای نقطه A، تعیین نوع پایداری یک کار بی اهمیت است. ریشه های معادله مشخصه λ1 =، λ2 = است. بنابراین ما چهار گزینه دریافت می کنیم:

1. λ1 > 0، λ2 > 0 - گره ناپایدار.

2.λ1< 0, λ2 >0 - زین.

3. λ1 ​​> 0، λ2< 0 - седло.

4.λ1< 0, λ2 < 0 - устойчивый узел.

با صحبت در مورد نقطه B، شایان ذکر است که جایگزین کردن اختصارات در عبارت برای آن، کار با ژاکوبین و یافتن ریشه های معادله مشخصه را پیچیده می کند. به عنوان مثال، پس از تلاش برای یافتن آنها با استفاده از ابزارهای محاسباتی WolframAlpha، خروجی ریشه ها حدود پنج خط طول کشید، که اجازه کار با آنها را به صورت تحت اللفظی نمی دهد. البته، اگر پارامترهای موجود از قبل وجود داشته باشد، یافتن سریع یک نقطه تعادل ممکن به نظر می رسد، اما این یک مورد خاص است، زیرا ما وضعیت تعادل را، در صورت وجود، فقط برای این پارامترها خواهیم یافت، که برای تصمیم گیری مناسب نیست. سیستم پشتیبانی که مدل برای ایجاد آن برنامه ریزی شده است.

با توجه به پیچیدگی کار با ریشه های معادله مشخصه، ما ترتیب متقابل ایزوکلین های صفر را با قیاس با سیستم تحلیل شده در کار بازیکین می سازیم (بازیکین، 2003). این به ما اجازه می دهد تا حالت های احتمالی سیستم را در نظر بگیریم و در آینده هنگام ساخت پرتره های فاز، نقاط تعادل و انواع پایداری آنها را پیدا کنیم.

پس از انجام برخی محاسبات، معادلات ایزوکلینیک صفر به شکل زیر در می آیند:

(2.7)

بنابراین ایزوکلین ها شکل سهمی دارند.

شکل 2.3. مکان ایزوکلینیک تهی احتمالی

در مجموع، چهار مورد احتمالی از آرایش متقابل آنها با توجه به تعداد نقاط مشترک بین سهمی ها وجود دارد. هر یک از آنها مجموعه پارامترهای خاص خود را دارند و از این رو پرتره های فازی سیستم هستند.

2 پرتره فازی از سیستم ها

اجازه دهید یک پرتره فازی از سیستم بسازیم، به شرط آن و پارامترهای باقیمانده برابر با 1 هستند. در این مورد، یک مجموعه از متغیرها کافی است، زیرا کیفیت تغییر نخواهد کرد.

همانطور که از شکل های زیر مشاهده می شود، نقطه صفر یک گره ناپایدار است و نقطه دوم، اگر مقادیر عددی پارامترها را جایگزین کنیم، (-1.5، -1.5) - یک زین می شود.

شکل 2.4. پرتره فاز برای سیستم (2.2)

بنابراین، از آنجایی که هیچ تغییری نباید رخ دهد، برای این سیستم فقط حالت های ناپایدار وجود دارد که به احتمال زیاد به دلیل امکان رشد نامحدود است.

یک مدل عملیات اولیه با دو محدودیت.

در این سیستم یک عامل محدود کننده اضافی وجود دارد، بنابراین نمودارهای فاز باید با حالت قبلی متفاوت باشد، همانطور که در شکل مشاهده می شود. نقطه صفر نیز یک گره ناپایدار است، اما یک موقعیت پایدار در این سیستم ظاهر می شود، یعنی یک گره پایدار. با این پارامترها مختصات آن (5.5،5.5) در شکل نشان داده شده است.

شکل 2.5. پرتره فاز برای سیستم (2.3)

بنابراین، محدودیت در هر اصطلاح، به دست آوردن یک موقعیت پایدار از سیستم را ممکن کرد.

مدل عملیات اولیه توسعه یافته

بیایید پرتره های فازی را برای مدل توسعه یافته بسازیم، اما بلافاصله با استفاده از شکل اصلاح شده آن:

اجازه دهید چهار مجموعه از پارامترها را در نظر بگیریم، مانند در نظر گرفتن همه موارد با نقطه تعادل صفر، و همچنین برای نشان دادن نمودارهای فاز شبیه سازی عددی مورد استفاده برای یک نقطه تعادل غیر صفر: مجموعه A (1،0.5،0.5) مربوط به دولت است ، مجموعه B(1,0.5,-0.5) مربوط به تنظیم C(-1.0.5، 0.5) و تنظیم D(-1.0.5،-0.5) ، یعنی یک گره پایدار در نقطه صفر. دو مجموعه اول پرتره های فاز را برای پارامترهایی که در شبیه سازی عددی در نظر گرفته ایم نشان می دهد.

شکل 2.6. پرتره فاز برای سیستم (2.4) با پارامترهای А-D.

در شکل ها توجه به نقاط (-1،2) و (1--2) به ترتیب ضروری است که در آنها یک "زین" ظاهر می شود. برای نمایش دقیق تر، شکل یک مقیاس متفاوت از شکل را با نقطه زین (1،-2) نشان می دهد. در شکل، در نقاط (1،2) و (-1،-2)، یک مرکز پایدار قابل مشاهده است. در مورد نقطه صفر، با شروع از شکل به شکل در نمودارهای فاز، می توانیم به وضوح یک گره ناپایدار، یک زین، یک زین و یک گره پایدار را تشخیص دهیم.

مدل همکاری اولیه توسعه یافته با محدودیت لجستیک

مانند مدل قبلی، پرتره های فازی را برای چهار حالت نقطه صفر نشان خواهیم داد و همچنین سعی خواهیم کرد راه حل های غیر صفر را در این نمودارها یادداشت کنیم. برای انجام این کار، مجموعه پارامترهای زیر را با پارامترهای مشخص شده به ترتیب زیر (): A (2،1،2،1)، B (2،1،1،2)، C (1،2،2) ,1) و D (1,2,1,2). پارامترهای باقیمانده برای همه مجموعه ها به صورت زیر خواهد بود: .

در شکل‌های ارائه‌شده در زیر، می‌توان چهار حالت تعادل نقطه صفر که در بخش قبل برای این سیستم دینامیکی توضیح داده شد را مشاهده کرد. و همچنین در شکل ها موقعیت پایدار یک نقطه با یک مختصات غیر صفر.

شکل 2.7. پرتره فاز برای سیستم (2.5) با پارامترهای A-B

3 مسیر یکپارچه سیستم ها

مدل عملیات اولیه با محدودیت Verhulst

همانطور که در فصل قبل هر یک از معادلات دیفرانسیل را جداگانه حل می کنیم و وابستگی متغیرها را به پارامتر زمان به صراحت بیان می کنیم.

(2.8)

(2.9)

از معادلات به دست آمده می توان دریافت که مقدار هر یک از متغیرها افزایش می یابد که در مدل سه بعدی زیر نشان داده شده است.

شکل 2.8. مدل سه بعدی برای معادله (2.8)

این نوع نمودار در ابتدا شبیه مدل مالتوسی سه بعدی غیراشباع است که در فصل 1 مورد بحث قرار گرفت، زیرا رشد سریع مشابهی دارد، اما بعداً با رسیدن به حد خروجی، می توانید کاهش نرخ رشد را مشاهده کنید. بنابراین ظاهر نهایی منحنی های انتگرال شبیه به نمودار معادله لجستیکی است که برای محدود کردن یکی از اصطلاحات استفاده شد.

یک مدل عملیات اولیه با دو محدودیت.

ما هر یک از معادلات را با استفاده از ابزار Wolfram Alpha حل می کنیم. بنابراین، وابستگی تابع x(t) به شکل زیر کاهش می یابد:

(2.10)

برای تابع دوم، وضعیت مشابه است، بنابراین راه حل آن را حذف می کنیم. مقادیر عددی به دلیل جایگزینی پارامترها با مقادیر مناسب خاص ظاهر می شوند که بر رفتار کیفی منحنی های انتگرال تأثیر نمی گذارد. نمودارهای زیر استفاده از محدودیت‌ها در رشد را نشان می‌دهند زیرا رشد نمایی در طول زمان لگاریتمی می‌شود.

شکل 2.9. مدل سه بعدی برای معادله (2.10)

مدل عملیات اولیه توسعه یافته

تقریباً شبیه به مدل های متقابل. تنها تفاوت در رشد سریعتر نسبت به آن مدل ها است که از معادلات زیر (اگر به درجه توان نگاه کنید) و نمودارها قابل مشاهده است. منحنی انتگرال باید به شکل یک توان باشد.

(2.11)

(2.12)

مدل همکاری اولیه توسعه یافته با محدودیت لجستیک

وابستگی x(t) به شکل زیر است:

بدون نمودار، ارزیابی رفتار تابع دشوار است، بنابراین با استفاده از ابزارهایی که قبلاً برای ما شناخته شده است، آن را می سازیم.

شکل 2.10 مدل سه بعدی برای معادله

مقدار تابع برای مقادیر غیر کوچک یک متغیر دیگر کاهش می یابد که به دلیل عدم وجود محدودیت در عبارت دوخطی منفی است و یک نتیجه واضح است.

4 پویایی سیستم شرکت های در حال تعامل

مدل عملیات اولیه با محدودیت Verhulst.

اجازه دهید سیستم (2.2) را بسازیم. با استفاده از ابزارهایی که قبلاً برای ما شناخته شده است، یک مدل شبیه سازی می سازیم. این بار بر خلاف مدل های متقابل، مدل دارای محدودیت لجستیکی خواهد بود.

شکل 2.11. مدل دینامیک سیستم برای سیستم (2.2)

بیایید مدل را اجرا کنیم. در این مدل، شایان ذکر است که رشد حاصل از رابطه با هیچ چیز محدود نمی شود و رشد بازده بدون تأثیر دیگری دارای محدودیت خاصی است. اگر به بیان خود تابع لجستیک نگاه کنید، می بینید که در حالتی که متغیر (تعداد کالا) از حداکثر حجم ذخیره سازی ممکن بیشتر شود، عبارت منفی می شود. در مواردی که فقط یک عملکرد لجستیک وجود دارد، این غیرممکن است، اما با یک عامل رشد همیشه مثبت اضافی، این امکان پذیر است. و اکنون مهم است که درک کنیم که عملکرد لجستیک با وضعیت رشد نه چندان سریع تعداد محصولات، به عنوان مثال، خطی مقابله خواهد کرد. بیایید نگاهی به تصاویر زیر بیاندازیم.

شکل 2.12. نمونه ای از عملکرد مدل دینامیک سیستم برای سیستم (2.2)

شکل سمت چپ گام پنجم برنامه مربوط به مدل پیشنهادی را نشان می دهد. اما در حال حاضر ارزش توجه به رقم مناسب را دارد.

ابتدا، برای یکی از جریان های ورودی برای Y_stock، پیوند x که بر حسب , بیان شده است حذف شده است. این کار به منظور نشان دادن تفاوت عملکرد مدل با جریان خطی همیشه مثبت و رشد دو خطی انجام می شود که برای X_stock ارائه شده است. با جریان های نامحدود خطی، پس از فراتر رفتن از پارامتر K، سیستم در نقطه ای به حالت تعادل می رسد (در این مدل حالت تعادل 200 هزار واحد کالا است). اما خیلی زودتر، رشد دو خطی منجر به افزایش شدید تعداد کالاها می شود و به بی نهایت می رسد. اگر هر دو سمت راست و چپ را دائماً جریان مثبت دوخطی بگذاریم، در حال حاضر در حدود 20-30 مرحله، مقدار انباشته به اختلاف دو بی نهایت می رسد.

با توجه به موارد فوق، به جرات می توان گفت که در صورت استفاده بیشتر از این گونه مدل ها، باید هرگونه رشد مثبت را محدود کرد.

یک مدل عملیات اولیه با دو محدودیت.

با پی بردن به کاستی های مدل قبلی و ایجاد محدودیت در ترم دوم توسط ضریب اشباع، مدل جدیدی را ساخته و اجرا می کنیم.

شکل 2.13. مدل دینامیک سیستم و نمونه ای از عملکرد آن برای سیستم (2.3)

این مدل در نهایت نتایج مورد انتظار را به ارمغان می آورد. معلوم شد که رشد مقادیر انباشته را محدود می کند. همانطور که از شکل سمت راست مشاهده می شود، برای هر دو شرکت، تعادل با مقدار کمی بیش از حد ذخیره سازی حاصل می شود.

مدل عملیات اولیه توسعه یافته

هنگام در نظر گرفتن پویایی سیستم این مدل، قابلیت های محیط نرم افزار AnyLogic برای تجسم رنگارنگ مدل ها نشان داده می شود. تمام مدل های قبلی تنها با استفاده از عناصر دینامیک سیستم ساخته شده اند. بنابراین، خود مدل ها محجوب به نظر می رسیدند، آنها اجازه ردیابی پویایی تغییرات در میزان تولید در طول زمان و تغییر پارامترها را در حین اجرای برنامه نمی دادند. هنگام کار با این مدل و مدل های بعدی، سعی می کنیم از طیف وسیع تری از قابلیت های برنامه برای تغییر سه نقطه ضعف فوق استفاده کنیم.

در مرحله اول، علاوه بر بخش "سیستم دینامیک"، این برنامه همچنین شامل بخش های "تصاویر"، "اشیاء سه بعدی" است که تنوع مدل را ممکن می کند، که برای ارائه بیشتر آن مفید است، زیرا مدل را می سازد. "دلپذیرتر" به نظر برسید.

در مرحله دوم، برای پیگیری پویایی تغییرات در مقادیر مدل، یک بخش "آمار" وجود دارد که به شما امکان می دهد نمودارها و ابزارهای مختلف جمع آوری داده ها را با پیوند دادن آنها به مدل اضافه کنید.

ثالثاً برای تغییر پارامترها و سایر اشیاء در حین اجرای مدل، بخش "کنترل" وجود دارد. اشیاء موجود در این بخش به شما امکان می دهند هنگام اجرای مدل، پارامترها را تغییر دهید (به عنوان مثال، "slider")، حالت های مختلف شی را انتخاب کنید (به عنوان مثال، "switch") و اقدامات دیگری را انجام دهید که داده های اولیه مشخص شده را در طول کار تغییر می دهد. .

این مدل برای آموزش آشنایی با پویایی تغییرات در تولید شرکت ها مناسب است، اما عدم محدودیت در رشد اجازه استفاده از آن را در عمل نمی دهد.

مدل همکاری اولیه توسعه یافته با محدودیت لجستیک

با استفاده از مدل قبلی آماده شده، پارامترهایی را از معادله لجستیک اضافه می کنیم تا رشد را محدود کنیم.

ما ساخت مدل را حذف می کنیم، زیرا پنج مدل قبلی ارائه شده در کار قبلاً تمام ابزارها و اصول لازم برای کار با آنها را نشان داده اند. فقط شایان ذکر است که رفتار آن مشابه مدل همکاری اولیه با محدودیت Verhulst است. آن ها عدم اشباع مانع کاربرد عملی آن می شود.

پس از تجزیه و تحلیل مدل ها از نظر همکاری اولیه، چندین نکته اصلی را تعریف می کنیم:

مدل‌هایی که در این فصل در نظر گرفته شده‌اند، در عمل مناسب‌تر از مدل‌های متقابل هستند، زیرا آن‌ها موقعیت‌های تعادلی پایدار غیر صفر را حتی با دو عبارت دارند. یادآوری می کنم که در مدل های متقابل، تنها با افزودن ترم سوم توانستیم به این مهم برسیم.

مدل‌های مناسب باید محدودیت‌هایی برای هر یک از اصطلاحات داشته باشند، زیرا در غیر این صورت، افزایش شدید فاکتورهای دوخطی، کل مدل شبیه‌سازی را از بین می‌برد.

با توجه به پاراگراف 2، هنگام اضافه کردن یک عملیات اولیه با محدودیت Verhulst از ضریب اشباع به مدل توسعه یافته، و همچنین افزودن مقدار بحرانی کمتری از تولید، مدل باید تا حد امکان به وضعیت واقعی نزدیک شود. اما فراموش نکنید که چنین دستکاری های سیستم تحلیل آن را پیچیده می کند.

نتیجه

در نتیجه این مطالعه، تجزیه و تحلیلی از شش سیستم انجام شد که پویایی تولید را توسط شرکت هایی که متقابلاً بر یکدیگر تأثیر می گذارند، توصیف می کنند. در نتیجه، نقاط تعادل و انواع پایداری آنها به یکی از روش های زیر تعیین شد: تحلیلی، یا به لطف پرتره های فاز ساخته شده در مواردی که راه حل تحلیلی به دلایلی امکان پذیر نیست. برای هر یک از سیستم ها نمودارهای فازی ساخته شد و همچنین مدل های سه بعدی ساخته شد که در هنگام طرح ریزی می توان منحنی های انتگرال را در صفحات (x, t), (y, t) به دست آورد. پس از آن، با استفاده از محیط مدل‌سازی AnyLogic، تمامی مدل‌ها ساخته شدند و گزینه‌های رفتاری آن‌ها تحت پارامترهای خاصی در نظر گرفته شد.

پس از تجزیه و تحلیل سیستم‌ها و ساخت مدل‌های شبیه‌سازی آن‌ها، مشخص می‌شود که این مدل‌ها به دلیل دقت پایین و در برخی مکان‌ها فقط می‌توانند به عنوان آموزش یا برای توصیف سیستم‌های ماکروسکوپی در نظر گرفته شوند، اما نه به عنوان یک سیستم پشتیبانی تصمیم برای شرکت‌ها. نمایش کاملا قابل اعتمادی از فرآیندهای در حال انجام نیست. اما همچنین فراموش نکنید که هر چقدر هم که سیستم دینامیکی توصیف‌کننده مدل درست باشد، هر شرکت/سازمان/صنعت فرآیندها و محدودیت‌های خاص خود را دارد، بنابراین نمی‌توان یک مدل کلی ایجاد و توصیف کرد. در هر مورد خاص، اصلاح می شود: پیچیده تر شود یا برعکس، برای کار بیشتر ساده شود.

با نتیجه گیری از نتیجه گیری برای هر فصل، ارزش تمرکز بر این واقعیت آشکار را دارد که معرفی محدودیت ها در هر یک از شرایط معادله، اگرچه سیستم را پیچیده می کند، اما به شما امکان می دهد موقعیت های پایدار سیستم را نیز تشخیص دهید. و همچنین آن را به آنچه در واقعیت اتفاق می افتد نزدیکتر کند. و شایان ذکر است که مدل‌های همکاری اولیه برای مطالعه مناسب‌تر هستند، زیرا برخلاف دو مدل متقابلی که در نظر گرفتیم، موقعیت‌های پایدار غیر صفر دارند.

بدین ترتیب هدف این مطالعه محقق شد و تکالیف تکمیل شد. در آینده، به عنوان ادامه این کار، یک مدل توسعه یافته از تعامل نوع عملیات اولیه با سه محدودیت معرفی شده بر روی آن در نظر گرفته می شود: لجستیک، ضریب اشباع، عدد بحرانی پایین تر، که باید امکان ایجاد دقیق تر را فراهم کند. مدلی برای یک سیستم پشتیبانی تصمیم، و همچنین مدلی با سه شرکت. به عنوان امتداد کار می توان به غیر از همزیستی دو نوع تعامل دیگر را نیز در نظر گرفت که در اثر به آنها اشاره شد.

ادبیات

1. بهاتیا نام پرشاد; Szegh Giorgio P. (2002). تئوری پایداری سیستم های دینامیکی. اسپرینگر.

2. بلانچارد پی. دوانی، آر. ال. هال، جی آر (2006). معادلات دیفرانسیل. لندن: تامپسون. pp. 96-111.

بوئینگ، جی (2016). تحلیل بصری سیستم‌های دینامیکی غیرخطی: آشوب، فراکتال‌ها، خود شباهت و محدودیت‌های پیش‌بینی. سیستم های. 4 (4): 37.

4. کمپبل، دیوید کی (2004). فیزیک غیر خطی: نفس تازه. طبیعت. 432 (7016): 455-456.

التون سی.اس. (1968) تجدید چاپ. اکولوژی حیوانات بریتانیای کبیر: ویلیام کلوز و پسران با مسئولیت محدود.

7. Forrester Jay W. (1961). دینامیک صنعتی مطبوعات MIT.

8. گاندولفو، جیانکارلو (1996). پویایی اقتصادی (ویرایش سوم). برلین: اسپرینگر. pp. 407-428.

9. Gershenfeld Neil A. (1999). ماهیت مدلسازی ریاضی. کمبریج، انگلستان: انتشارات دانشگاه کمبریج.

10 گودمن ام (1989). نکات مطالعه در دینامیک سیستم. پگاسوس

Grebogi C، Ott E و Yorke J. (1987). آشوب، جاذبه های عجیب و غریب، و مرزهای حوضه فراکتال در دینامیک غیرخطی. علم 238 (4827)، ص 632-638.

12 Hairer Ernst; نورست سیورت پل; وانر، گرهارد (1993)، حل معادلات دیفرانسیل معمولی I: مسائل غیر سخت، برلین، نیویورک

Hanski I. (1999) محیط زیست فراجمعیت. انتشارات دانشگاه آکسفورد، آکسفورد، ص. 43-46.

هیوز-هلت دبورا; مک کالوم، ویلیام جی. گلیسون، اندرو ام (2013). حساب دیفرانسیل و انتگرال: تک و چند متغیره (6 ویرایش). جان وایلی.

15. Llibre J., Valls C. (2007). اولین انتگرال های تحلیلی جهانی برای سیستم مسطح واقعی Lotka-Volterra، J. Math. فیزیک

16. جردن دی. اسمیت پی (2007). معادلات دیفرانسیل معمولی غیر خطی: مقدمه ای برای دانشمندان و مهندسان (ویرایش چهارم). انتشارات دانشگاه آکسفورد.

خلیل حسن ک (1380). سیستم های غیر خطی سالن پرنتیس

دانشگاه لامار، یادداشت‌های ریاضی آنلاین - هواپیمای فاز، پی داوکینز.

دانشگاه لامار، یادداشت‌های ریاضی آنلاین - سیستم‌های معادلات دیفرانسیل، پی داوکینز.

لانگ سرژ (1972). منیفولدهای دیفرانسیل Reading, Mass.-London-Don Mills, Ont.: Addison-Wesley Publishing Co., Inc.

Law Averill M. (2006). شبیه سازی مدل سازی و تحلیل با نرم افزار Expertfit. علم مک گراو-هیل.

Lazard D. (2009). سی سال حل سیستم چند جمله ای، و اکنون؟ مجله محاسبات نمادین. 44 (3): 222-231.

24 لوئیس مارک دی (2000). نوید رویکردهای سیستم های پویا برای یک حساب یکپارچه توسعه انسانی. رشد کودک. 71 (1): 36-43.

25. مالتوس تی.آر. (1798). مقاله ای در مورد اصل جمعیت، در کتاب کلاسیک جهان آکسفورد، ص 61، پایان فصل هفتم

26. مورکرافت جان (2007). مدل‌سازی استراتژیک و پویایی کسب‌وکار: رویکرد سیستم‌های بازخورد. جان وایلی و پسران

27. Nolte D.D. (2015)، مقدمه ای بر دینامیک مدرن: آشوب، شبکه ها، فضا و زمان، انتشارات دانشگاه آکسفورد.

مقدمه 4

تجزیه و تحلیل پیشینی سیستم های دینامیکی 5

عبور یک سیگنال تصادفی از یک سیستم خطی 5

تکامل بردار فاز سیستم 7

تکامل ماتریس کوواریانس بردار فاز سیستم 8

خطی سازی آماری 8

راه اول 9

راه دوم 10

محاسبه ضرایب خطی سازی 10

ابهام در پیوندهای غیر خطی 14

پیوند غیرخطی تحت پوشش بازخورد 15

شبیه سازی فرآیندهای تصادفی 16

فیلتر شکل دهی 16

مدلسازی نویز سفید 17

برآورد ویژگی های آماری سیستم های دینامیکی به روش مونت کارلو 18

دقت نمره 18

سیستم های دینامیکی غیر ساکن 20

سیستم های دینامیکی ساکن 21

تحلیل پسینی سیستم های دینامیکی 22

فیلتر کالمن 22

الگوی حرکت 22

مدل اندازه گیری 23

تصحیح 23

پیش بینی 23

کلاس 23

استفاده از فیلتر کالمن در مسائل غیرخطی 25

حداقل مربع 27

کلاس ساختمان 27

پیش بینی 29

استفاده از روش حداقل مربعات در مسائل غیرخطی 29

ساخت ماتریس کوشی 30

مدل سازی اندازه گیری 30

روش های عددی 31

توابع ویژه 31

شبیه سازی متغیرهای تصادفی 31

متغیرهای تصادفی توزیع شده یکنواخت 31

متغیرهای تصادفی گاوسی 32

بردارهای تصادفی 33

انتگرال احتمالات 34

چند جمله ای های چبیشف 36

ادغام معادلات دیفرانسیل معمولی 36

روش های رانگ-کوتا 36

دقت نتایج یکپارچه سازی عددی 37

سفارش تودرتو Dorman-Prince 5(4) 37

روش های چند مرحله ای 39

روش های آدامز 39

ادغام معادلات تاخیری 40

مقایسه کیفیت های محاسباتی روش ها 40

مشکل آرنستورف 40

توابع بیضوی ژاکوبی 41

مشکل دو تنه 41

معادله ون در پل 42

Brusselator 42

ریسمان آویزان معادله لاگرانژ 42

Pleiades 42

ایجاد یادداشت توضیحی 43

عنوان صفحه 43

بخش "مقدمه" 44

بخش "نظریه" 44

بخش "الگوریتم" 44

بخش "برنامه" 45

بخش "نتایج" 45

بخش "نتیجه گیری" 45

بخش "فهرست منابع مورد استفاده" 45

برنامه های کاربردی 45

ادبیات 47

معرفی

این راهنما حاوی دستورالعمل‌هایی برای تکمیل تکالیف پروژه‌های درسی و انجام تمرین‌های عملی در درس «مبانی دینامیک آماری» است.

هدف از طراحی دوره و تمرین های عملی تسلط بر فناوری تحلیل پیشینی و پسینی سیستم های دینامیکی غیرخطی تحت تأثیر اغتشاشات تصادفی است.

تحلیل پیشینی سیستم های دینامیکی

خطی سازی آماری

خطی سازی آماری به شما امکان می دهد سیستم دینامیکی غیرخطی اصلی را به گونه ای تبدیل کنید که برای تجزیه و تحلیل آن می توان از روش ها، الگوریتم ها و روابط معتبر برای سیستم های خطی استفاده کرد.

این بخش به ارائه روش خطی سازی آماری، بر اساس ساده ترین رویکرد تقریبی ارائه شده توسط پروفسور اختصاص داده شده است. I.E. کازاکوف، که با این وجود، امکان ساخت تخمین‌هایی از دقت سیستمی را فراهم می‌کند که حتی غیرخطی‌های قابل توجهی با ویژگی‌های ناپیوسته دارد.

خطی‌سازی آماری شامل جایگزینی وابستگی غیرخطی بدون اینرسی اصلی بین فرآیندهای ورودی و خروجی با چنین وابستگی تقریبی، خطی با توجه به فرآیند تصادفی ورودی متمرکز است که از نظر آماری با فرآیند اصلی معادل است:

پیوندی که چنین رابطه تقریبی بین سیگنال های ورودی و خروجی داشته باشد، معادل پیوند غیرخطی در نظر گرفته می شود.

مقدار بر اساس شرط برابری انتظارات ریاضی سیگنال های غیر خطی و خطی انتخاب می شود و مشخصه میانگین آماری پیوند معادل نامیده می شود:

,

چگالی توزیع سیگنال ورودی کجاست.

برای پیوندهای غیر خطی با ویژگی های فرد، به عنوان مثال. در ، راحت است که مشخصه آماری را به شکل زیر نشان دهیم:

انتظار ریاضی از سیگنال ورودی است.
سود آماری پیوند معادل بر حسب جزء متوسط ​​است.

که وابستگی معادل در این مورد به شکل زیر است:

مشخصه، بهره آماری پیوند معادل برای جزء تصادفی (نوسانات) نامیده می شود و به دو صورت تعیین می شود.

راه اول

مطابق با روش اول خطی سازی آماری، ضریب بر اساس شرط برابری پراکندگی سیگنال های اصلی و معادل انتخاب می شود. که برای محاسبه رابطه زیر را بدست می آوریم:

,

واریانس عمل تصادفی ورودی کجاست.

علامت در عبارت for با ماهیت وابستگی در مجاورت مقدار استدلال تعیین می شود. اگر افزایش یابد، پس، و اگر کاهش یابد، پس .

راه دوم

مقدار طبق روش دوم از شرط کمینه سازی میانگین خطای خطی مربعات انتخاب می شود:

نسبت نهایی برای محاسبه ضریب به روش دوم:

.

در نتیجه، ما متذکر می شویم که هیچ یک از دو روش خطی سازی در نظر گرفته شده در بالا، برابری توابع همبستگی سیگنال های خروجی لینک های غیر خطی و معادل را تضمین نمی کند. محاسبات نشان می‌دهد که برای تابع همبستگی یک سیگنال غیرخطی، روش انتخاب اول تخمین بالایی را ارائه می‌دهد و روش دوم تخمین پایین‌تری را ارائه می‌دهد، یعنی. خطاها در تعیین تابع همبستگی سیگنال خروجی غیرخطی علائم مختلفی دارند. پروفسور I.E. کازاکوف، نویسنده روش شرح داده شده در اینجا، توصیه می کند که به عنوان ضریب خطی سازی حاصل، نصف ضرایب به دست آمده توسط روش اول و دوم را انتخاب کنید.

فیلتر شکل دهی

به طور معمول، پارامترها با معادل سازی ضرایب چند جمله ای های صورت و مخرج در معادله تعیین می شوند.

با همان درجات

پس از تعیین تابع انتقال فیلتر شکل‌دهی، طرح حاصل برای مدل‌سازی یک فرآیند تصادفی مطابق شکل به نظر می‌رسد.

برای مثال، چگالی طیفی فرآیندی که باید مدل‌سازی شود به شکل زیر است:

,

انتظارات ریاضی و نویز سفید با شدت برای مدل‌سازی استفاده می‌شود، بنابراین چگالی طیفی واحد دارد.

بدیهی است که صورت و مخرج تابع انتقال مورد نظر باید دارای دستورات 1 و 2 باشد (در واقع تابع انتقال با مجذور بودن مدول، ضریبی از چندجمله ای های درجه 2 و 4 را تشکیل می دهد).

که عملکرد انتقال فیلتر شکل دهنده در کلی ترین شکل آن به شرح زیر است:

,

و مربع مدول آن:

اجازه دهید نسبت های به دست آمده را معادل سازی کنیم:

اجازه دهید براکت ها و در سمت راست تساوی را برداریم و بدین ترتیب ضرایب را در صفر درجه برابر کنیم:

,

از این رو تساوی های زیر به وضوح دنبال می شوند:

; ; ; .

که بلوک دیاگرام تشکیل یک فرآیند تصادفی با ویژگی های آماری داده شده از نویز سفید با چگالی طیفی واحد همانطور که در شکل نشان داده شده است، با در نظر گرفتن مقادیر محاسبه شده پارامترهای فیلتر شکل دهی به نظر می رسد.

مدلسازی نویز سفید

برای شبیه سازی یک فرآیند تصادفی با ویژگی های آماری داده شده، نویز سفید به عنوان یک فرآیند تصادفی ورودی به فیلتر شکل دهی استفاده می شود. با این حال، مدل‌سازی دقیق نویز سفید به دلیل واریانس بی‌نهایت این فرآیند تصادفی امکان‌پذیر نیست.

به همین دلیل، یک فرآیند گام تصادفی به عنوان جایگزینی برای نویز سفید که بر روی سیستم دینامیکی عمل می کند استفاده می شود. فاصله ای که اجرای یک فرآیند تصادفی مقدار آن را بدون تغییر نگه می دارد (عرض گام، فاصله همبستگی) یک مقدار ثابت است. مقادیر پیاده سازی خود (ارتفاع گام) متغیرهای تصادفی هستند که بر اساس قانون عادی با انتظارات ریاضی صفر و واریانس محدود توزیع شده اند. مقادیر پارامترهای فرآیند - فاصله همبستگی و پراکندگی - توسط ویژگی های سیستم پویا تعیین می شود که تحت تأثیر نویز سفید قرار می گیرد.

ایده روش مبتنی بر پهنای باند محدود هر سیستم دینامیکی واقعی است. آن ها بهره یک سیستم دینامیکی واقعی با افزایش فرکانس سیگنال ورودی کاهش می‌یابد، و بنابراین، فرکانس (کمتر از بینهایت) وجود دارد که بهره سیستم برای آن آنقدر کوچک است که می‌توان آن را روی صفر تنظیم کرد. و این به نوبه خود به این معنی است که سیگنال ورودی با چگالی طیفی ثابت، اما محدود با این فرکانس، برای چنین سیستمی معادل نویز سفید (با چگالی طیفی ثابت و بی نهایت) خواهد بود.

پارامترهای فرآیند تصادفی معادل - فاصله همبستگی و واریانس به صورت زیر محاسبه می شود:

مرز پهنای باند سیستم دینامیک به طور تجربی تعیین شده است.

دقت برآورد

برآورد انتظارات

و پراکندگی

متغیر تصادفی ساخته شده بر اساس پردازش نمونه محدودی از پیاده سازی های آن، خود متغیرهای تصادفی هستند.

بدیهی است که هرچه حجم نمونه پیاده سازی ها بزرگتر باشد، تخمین بی طرفانه دقیق تر، به مقدار واقعی پارامتر تخمین زده نزدیکتر است. در زیر فرمول های تقریبی بر اساس فرض توزیع نرمال آنها آورده شده است. فاصله اطمینان نسبی متقارن برای تخمین مربوط به احتمال اطمینان با مقداری که رابطه برای آن صادق است تعیین می شود:

,

جایی که
مقدار واقعی انتظارات ریاضی متغیر تصادفی است،
انحراف استاندارد متغیر تصادفی است،
انتگرال احتمال است.

بر اساس رابطه فوق، مقدار را می توان به صورت زیر تعیین کرد:

,

که در آن تابع با توجه به انتگرال احتمال معکوس است.

از آنجایی که دقیقاً مشخصه پراکندگی برآورد را نمی دانیم، از مقدار تقریبی آن که با استفاده از تخمین محاسبه می شود استفاده خواهیم کرد:

که رابطه نهایی که صحت برآورد انتظارات ریاضی و اندازه نمونه ای را که بر اساس آن تخمین زده می شود به هم مرتبط می کند به این صورت است:

.

این بدان معنی است که مقدار فاصله اطمینان (در یک مقدار ثابت احتمال اطمینان) که به طور متقارن در حدود قرار دارد، که در کسری از برآورد انحراف استاندارد بیان می شود، با جذر اندازه نمونه نسبت معکوس دارد.

فاصله اطمینان برای تخمین واریانس به روشی مشابه تعریف می شود:

تا مقدار، که در صورت عدم وجود اطلاعات دقیق تر، می توان تقریباً از رابطه زیر تعیین کرد:

که مقدار فاصله اطمینان (در یک مقدار ثابت احتمال اطمینان) که به طور متقارن با توجه به، بیان شده در سهام آن قرار دارد، به طور معکوس با جذر مقدار، که اندازه نمونه است، متناسب است.

با استفاده از اطلاعات دقیق در مورد قانون توزیع یک متغیر تصادفی می توان فرمول های دقیق تری برای ساخت فواصل اطمینان تخمین ها به دست آورد.

به عنوان مثال، برای قانون توزیع گاوس، متغیر تصادفی

از قانون توزیع دانشجو با درجه ای از آزادی و متغیر تصادفی پیروی می کند

طبق قانون نیز با درجه ای از آزادی توزیع می شود.

فیلتر کالمن

مدل حرکت

همانطور که می دانید فیلتر کالمن برای تخمین بردار حالت یک سیستم دینامیکی خطی طراحی شده است که مدل تکامل آن را می توان به صورت زیر نوشت:

جایی که
ماتریس کوشی است که تغییر بردار حالت سیستم را در حرکت خود (بدون اعمال کنترل و نویز) از لحظه به لحظه زمان تعیین می کند.
بردار اعمال اجباری غیر تصادفی روی سیستم (مثلاً اقدامات کنترلی) در لحظه زمان است.
ماتریس تأثیر اعمال اجباری در لحظه زمان بر بردار حالت سیستم در لحظه زمان است.
بردار اعمال متمرکز تصادفی مستقل بر روی سیستم در لحظه از زمان است.
ماتریس تأثیر تأثیرات تصادفی در لحظه زمان بر بردار حالت سیستم در لحظه زمان است.

مدل اندازه گیری

تخمین بر اساس پردازش آماری نتایج اندازه‌گیری انجام می‌شود که به صورت خطی با بردار حالت مرتبط است و توسط یک خطای بی‌طرفدار افزایشی تحریف شده است:

جایی که ماتریسی است که بردارهای حالت و اندازه گیری را همزمان به هم متصل می کند.

تصحیح

اساس فیلتر کالمن نسبت‌های اصلاحی است که نتیجه به حداقل رساندن رد ماتریس کوواریانس چگالی توزیع خلفی تخمین‌های خطی (در امتداد بردار اندازه‌گیری) بردار حالت سیستم است:

پیش بینی

تکمیل روابط تصحیح با روابط پیش بینی بر اساس ویژگی های خطی مدل تکامل سیستم:

ماتریس کوواریانس بردار کجاست , فرمولهایی برای الگوریتم بیزی تکراری برای تخمین بردار حالت سیستم و ماتریس کوواریانس آن بر اساس پردازش آماری نتایج اندازه گیری بدست می آوریم .

ارزیابی

بدیهی است که برای اجرای روابط فوق باید بتوان ماتریس هایی از مدل تکاملی، ماتریسی از مدل اندازه گیری و همچنین ماتریس های کوواریانس و برای هر لحظه از زمان ساخت.

علاوه بر این، برای مقداردهی اولیه فرآیند محاسباتی، لازم است به نحوی تخمین های پسینی یا پیشینی بردار حالت و ماتریس کوواریانس آن تعیین شود. اصطلاح "پیشینی" یا "پسینی" در این مورد فقط به معنای کیفیتی است که بردار حالت و ماتریس کوواریانس آن در الگوریتم محاسباتی استفاده خواهد شد و چیزی در مورد نحوه به دست آوردن آنها بیان نمی کند.

بنابراین، انتخاب نسبتی که از آن محاسبات باید شروع شود، با توجه به نقاط زمانی که شرایط فیلتر اولیه و اولین بردار اندازه‌گیری خام به آن اختصاص داده می‌شود، تعیین می‌شود. اگر نقاط زمانی منطبق باشند، ابتدا باید نسبت‌های تصحیح را برای اصلاح شرایط اولیه اعمال کرد، در غیر این صورت، ابتدا باید شرایط اولیه را با زمان اتصال اولین بردار اندازه‌گیری خام پیش‌بینی کرد.

اجازه دهید الگوریتم فیلتر کالمن را با کمک یک شکل توضیح دهیم.

در شکل، در محورهای مختصات، (در کانال حرکت) چندین مسیر احتمالی بردار فاز نشان داده شده است:

مسیر تکامل واقعی بردار فاز است.
تکامل بردار فاز است که بر اساس استفاده از مدل حرکت و تخمین پیشینی بردار فاز پیش‌بینی می‌شود که به زمان اشاره می‌کند.
تکامل بردار فاز است که بر اساس استفاده از مدل حرکت و تخمین پسینی (دقیق تر) بردار فاز پیش بینی شده است.

محورهای مختصات، (در کانال اندازه گیری) در لحظه های زمانی و نمایش نتایج اندازه گیری ها و :

,

جایی که
مقدار واقعی بردار اندازه گیری در زمان است.
بردار خطاهای اندازه گیری است که در لحظه زمان متوجه می شوند.

برای ایجاد تصحیح بردار فاز پیشینی سیستم، از تفاوت بین نتیجه اندازه‌گیری و مقداری که مطابق مدل اندازه‌گیری مسئله اندازه‌گیری می‌شود، استفاده می‌شود، اگر بردار فاز، در واقع، مقدار را گرفته باشد. در نتیجه اعمال روابط تصحیح برای تخمین های پیشینی، تخمین بردار فاز سیستم تا حدودی دقیق تر خواهد بود و مقدار را به خود می گیرد.

در لحظه از زمان، نتیجه پیش بینی به عنوان یک برآورد پیشینی استفاده می شود در مسیری که از بردار فاز می گذرد، مجدداً اختلاف اندازه گیری ساخته می شود که بر اساس آن مقدار پسینی و حتی دقیق تر محاسبه می شود و غیره. تا زمانی که بردارهای اندازه گیری برای پردازش وجود داشته باشد یا نیاز به پیش بینی رفتار بردار فاز وجود داشته باشد.

روش حداقل مربعات

این بخش روش حداقل مربعات را ارائه می دهد که برای تحلیل پسینی سیستم های دینامیکی اقتباس شده است.

امتیازات ساختمان

برای مدل خطی اندازه گیری های مساوی:

ما الگوریتم تخمین بردار فاز زیر را داریم:

.

در مورد اندازه‌گیری‌های نابرابر، ماتریس حاوی ضرایب وزن روی قطر را معرفی می‌کنیم. با در نظر گرفتن ضرایب وزنی، نسبت قبلی به شکل زیر خواهد بود:

.

اگر از ماتریس معکوس به ماتریس کوواریانس خطاهای اندازه گیری به عنوان ماتریس وزن استفاده کنیم، با در نظر گرفتن این واقعیت که به دست می آوریم:

.

همانطور که از روابط بالا بر می آید، اساس روش ماتریسی است که بردار فاز تخمین زده شده را به یک نقطه زمانی معین و بردار اندازه گیری مربوط می کند. بردار معمولاً یک ساختار بلوکی دارد که در آن هر یک از بلوک ها به نقطه ای از زمان اختصاص داده می شود که به طور کلی با .

شکل، آرایش متقابل احتمالی نقاط زمانی را که اندازه‌گیری‌ها به آن‌ها ارجاع داده می‌شود و نقطه زمانی که بردار پارامترهای برآورد شده به آن ارجاع داده می‌شود را نشان می‌دهد.

برای هر بردار، رابطه زیر معتبر است:

، در .

بنابراین، در رابطه حداقل مربعات حاصل، بردار و ماتریس ساختار زیر را دارند:

; .

جایی که
- یک اثر اجباری غیر تصادفی را بر روی سیستم تعیین می کند.
- تأثیر تصادفی روی سیستم را تعیین می کند.

می توان از روابط پیش بینی استفاده کرد که در بالا در توضیح الگوریتم فیلتر کالمن با آنها مواجه شدیم:

ماتریس کوواریانس بردار کجاست.

ساخت ماتریس کوشی

در مشکلات ساخت تخمین ها با روش های پردازش آماری اندازه گیری ها، مشکل ساخت ماتریس کوشی اغلب با مشکل مواجه می شود. این ماتریس بردارهای فاز سیستم را که به لحظه های مختلف زمان اشاره دارد را در حرکت خود به هم متصل می کند.

در این بخش، ما خود را به بررسی مسائل مربوط به ساخت ماتریس کوشی برای یک مدل تکاملی که به عنوان یک سیستم معادلات دیفرانسیل معمولی (خطی یا غیر خطی) نوشته شده است، محدود می کنیم.

که در آن از نماد زیر برای ماتریس های تناسب ساخته شده در مجاورت مسیر مرجع استفاده می شود، :

; .

مدل سازی ابعاد

مشکل زمانی به وجود می آید که، برای مثال، هنگام تخمین دقت بالقوه قابل دستیابی یک روش در یک مسئله، هیچ نتیجه اندازه گیری نداشته باشید. در این مورد، نتایج اندازه گیری باید شبیه سازی شود. ویژگی مدل‌سازی نتایج اندازه‌گیری این است که مدل‌های حرکت و اندازه‌گیری مورد استفاده برای این منظور ممکن است با مدل‌هایی که در طول ساخت تخمین‌ها با استفاده از یک یا آن روش فیلتر استفاده می‌کنید، مطابقت نداشته باشد.

به عنوان شرایط اولیه برای مدلسازی تکامل بردار فاز یک سیستم دینامیکی، باید از مقادیر واقعی مختصات این بردار استفاده شود. علاوه بر این مکان، مقادیر واقعی مختصات بردار فاز سیستم نباید در جای دیگری استفاده شود.

روشهای عددی

ویژگی های خاص

بردارهای تصادفی

مشکلی که راه حل آن در این بخش توضیح داده شده است، مدل سازی بردار متغیرهای تصادفی گاوسی همبسته است.

بگذارید بردار تصادفی که باید مدل‌سازی شود، بر اساس تبدیل بردار متغیرهای تصادفی استاندارد نامرتبط بعد مربوطه به صورت زیر تشکیل شود: با دقت 4 رقم، بر اساس بسط به سری در توان استدلال برای سه بازه آن

در , مجموع سری مجانبی تقریباً برابر با 1 می شود.