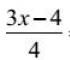وظایف برای کاربرد قضیه فیثاغورث. شروع در Science Doc در قضایای فیثاغورث

مطمئن شوید که مثلثی که به شما داده می شود مثلث قائم الزاویه باشد، زیرا قضیه فیثاغورث فقط برای مثلث های قائم الزاویه صدق می کند. در مثلث های قائم الزاویه یکی از سه زاویه همیشه 90 درجه است.

• زاویه قائمه در مثلث قائم الزاویه به جای منحنی با مربع نشان داده می شود که نشان دهنده زوایای غیر قائم است.

اضلاع مثلث را برچسب بزنید.پاها را به صورت "a" و "b" تعیین کنید (پاها اضلاع هستند که در زوایای قائم با هم متقاطع می شوند) و فرضیه را به عنوان "c" (هیپوتنوز بزرگترین ضلع مثلث قائم الزاویه است که در مقابل زاویه قائمه قرار دارد).

مشخص کنید که کدام ضلع مثلث را می خواهید پیدا کنید.قضیه فیثاغورث به شما امکان می دهد هر ضلعی از مثلث قائم الزاویه را بیابید (اگر دو ضلع دیگر آن مشخص باشد). تعیین کنید که کدام طرف (الف، ب، ج) باید پیدا شود.

• به عنوان مثال، با توجه به یک هیپوتانوس برابر با 5، و یک پا برابر با 3. در این مورد، شما باید پایه دوم را پیدا کنید. بعداً به این مثال باز خواهیم گشت.
• اگر دو ضلع دیگر مجهول باشند، باید طول یکی از ضلع های مجهول را پیدا کرد تا بتوان قضیه فیثاغورث را اعمال کرد. برای این کار از توابع مثلثاتی اصلی استفاده کنید (اگر مقدار یکی از زوایای غیر قائم به شما داده شود).

در فرمول a 2 + b 2 \u003d c 2 مقادیری را که به شما داده شده است (یا مقادیری که شما پیدا کرده اید) جایگزین کنید.به یاد داشته باشید که a و b پاها هستند و c هیپوتانوس است.

• در مثال ما بنویسید: 3² + b² = 5².

هر ضلع شناخته شده را مربع کنید.یا نماها را رها کنید - بعداً می توانید اعداد را مربع کنید.

• در مثال ما، بنویسید: 9 + b² = 25.

طرف مجهول را در یک طرف معادله جدا کنید.برای انجام این کار، مقادیر شناخته شده را به طرف دیگر معادله منتقل کنید. اگر فرضیه را پیدا کنید، در قضیه فیثاغورث قبلاً در یک طرف معادله جدا شده است (بنابراین هیچ کاری لازم نیست انجام شود).

• در مثال ما، عدد 9 را به سمت راست معادله ببرید تا مجهول b2 را جدا کنید. b² = 16 دریافت خواهید کرد.

جذر دو طرف معادله را بگیرید.در این مرحله در یک طرف معادله یک مجهول (مربع) و در طرف دیگر یک قطع (عدد) وجود دارد.

• در مثال ما، b² = 16. جذر هر دو طرف معادله را بگیرید و b = 4 را بدست آورید. بنابراین پای دوم برابر است با 4 .

از قضیه فیثاغورث در زندگی روزمره استفاده کنید، زیرا می توان آن را در تعداد زیادی از موقعیت های عملی به کار برد. برای انجام این کار، یاد بگیرید که مثلث های قائم الزاویه را در زندگی روزمره تشخیص دهید - در هر موقعیتی که در آن دو جسم (یا خط) با زوایای قائم تلاقی می کنند و جسم سوم (یا خط) بالای دو جسم اول (یا به صورت مورب) را به هم متصل می کند. خطوط)، می توانید از قضیه فیثاغورث برای یافتن ضلع مجهول (اگر دو ضلع دیگر شناخته شده باشند) استفاده کنید.

• مثال: با توجه به نردبانی که به ساختمان تکیه داده است. پایین پله ها از پایه دیوار 5 متر فاصله دارد. بالای پله ها از سطح زمین 20 متر (بالا از دیوار) فاصله دارد. طول نردبان چقدر است؟
  • «5 متر از پایه دیوار» یعنی a = 5; "20 متر از زمین است" به این معنی است که b = 20 (یعنی به شما دو پایه مثلث قائم الزاویه داده می شود، زیرا دیوار ساختمان و سطح زمین در زوایای قائمه همدیگر را قطع می کنند). طول نردبان طول هیپوتنوز است که ناشناخته است.
    • a² + b² = c²
    • (5)² + (20)² = c²
    • 25 + 400 = c²
    • 425 = c²
    • c = √425
    • c = 20.6. بنابراین، طول تقریبی پله ها است 20.6 متر.

کسانی که به تاریخ قضیه فیثاغورث که در برنامه درسی مدرسه مطالعه می شود علاقه مند هستند، در مورد واقعیتی مانند انتشار کتابی با سیصد و هفتاد دلیل از این قضیه به ظاهر ساده در سال 1940 نیز کنجکاو خواهند شد. اما ذهن بسیاری از ریاضیدانان و فیلسوفان دوره های مختلف را به خود مشغول کرد. در کتاب رکوردهای گینس به عنوان یک قضیه با حداکثر تعداد اثبات ثبت شده است.

تاریخچه قضیه فیثاغورث

این قضیه که با نام فیثاغورث مرتبط است، مدتها قبل از تولد فیلسوف بزرگ شناخته شده بود. بنابراین، در مصر، در هنگام ساخت سازه ها، نسبت اضلاع یک مثلث قائم الزاویه پنج هزار سال پیش در نظر گرفته شد. متون بابلی 1200 سال قبل از تولد فیثاغورث به همین نسبت اضلاع مثلث قائم الزاویه اشاره می کنند.

این سوال پیش می آید که چرا پس داستان می گوید - ظهور قضیه فیثاغورث متعلق به اوست؟ تنها یک پاسخ می تواند وجود داشته باشد - او نسبت اضلاع در مثلث را ثابت کرد. او کاری را انجام داد که قرن‌ها پیش کسانی که صرفاً از نسبت ابعاد و هیپوتنوس استفاده می‌کردند، انجام ندادند.

از زندگی فیثاغورث

دانشمند، ریاضیدان، فیلسوف بزرگ آینده در سال 570 قبل از میلاد در جزیره ساموس متولد شد. اسناد تاریخی اطلاعاتی را در مورد پدر فیثاغورث که یک گوهرتراش بود حفظ کرده است، اما از مادرش اطلاعاتی در دست نیست. آنها در مورد پسر متولد شده گفتند که او کودک برجسته ای بود که از کودکی به موسیقی و شعر علاقه نشان داد. مورخان هرمودامانت و فرکیدس اهل سیروس را به معلمان فیثاغورث جوان نسبت می دهند. اولی پسر را وارد دنیای موزها کرد و دومی که فیلسوف و بنیانگذار مکتب فلسفی ایتالیا بود، نگاه مرد جوان را به لوگوس معطوف کرد.

فیثاغورث در 22 سالگی (548 قبل از میلاد) برای مطالعه زبان و دین مصریان به ناوکراتیس رفت. علاوه بر این، مسیر او در ممفیس بود، جایی که به لطف کشیشان، پس از گذراندن آزمایش های مبتکرانه آنها، هندسه مصری را درک کرد، که شاید این مرد جوان کنجکاو را بر آن داشت تا قضیه فیثاغورث را اثبات کند. تاریخ بعداً این نام را به قضیه نسبت می دهد.

توسط پادشاه بابل اسیر شد

فیثاغورث در راه خانه خود به هلاس توسط پادشاه بابل اسیر می شود. اما بودن در اسارت به نفع ذهن کنجکاو ریاضیدان تازه کار بود، او چیزهای زیادی برای یادگیری داشت. در واقع، در آن سال ها، ریاضیات در بابل بیش از مصر توسعه یافته بود. او دوازده سال را صرف مطالعه ریاضیات، هندسه و جادو کرد. و شاید این هندسه بابلی بود که در اثبات نسبت اضلاع مثلث و تاریخچه کشف قضیه دخالت داشت. فیثاغورث دانش و زمان کافی برای این کار داشت. اما اینکه این اتفاق در بابل رخ داده است، هیچ تایید یا تکذیب مستندی در این مورد وجود ندارد.

در سال 530 ق.م فیثاغورث از اسارت به سرزمین خود می گریزد و در آنجا در دربار پلیکراتس ظالم در مقام نیمه برده زندگی می کند. چنین زندگی مناسب فیثاغورس نیست و او به غارهای ساموس بازنشسته می شود و سپس به جنوب ایتالیا می رود، جایی که در آن زمان مستعمره یونانی کروتون در آن قرار داشت.

دستور رهبانی مخفی

فیثاغورث بر اساس این مستعمره یک نظام رهبانی مخفی را تشکیل داد که در عین حال یک اتحادیه مذهبی و یک انجمن علمی بود. این جامعه اساسنامه خود را داشت که در آن از رعایت سبک زندگی خاص صحبت شده بود.

فیثاغورث استدلال می کرد که برای درک خدا، انسان باید علومی مانند جبر و هندسه را بداند، نجوم را بداند و موسیقی را درک کند. کار پژوهشی به شناخت جنبه عرفانی اعداد و فلسفه خلاصه شد. لازم به ذکر است که اصولی که در آن زمان توسط فیثاغورث موعظه می شد در زمان حاضر به صورت تقلید معنا پیدا می کند.

بسیاری از اکتشافات شاگردان فیثاغورث به او نسبت داده شد. با این وجود، به طور خلاصه، تاریخچه ایجاد قضیه فیثاغورث توسط مورخان و شرح حال نویسان باستانی آن زمان، مستقیماً با نام این فیلسوف، متفکر و ریاضیدان مرتبط است.

آموزه های فیثاغورث

شاید مورخان از بیانیه یونانی بزرگ الهام گرفته باشند که مثلث ضرب المثلی با پاها و هیپوتونوس آن همه پدیده های زندگی ما را رمزگذاری می کند. و این مثلث «کلید» حل تمام مشکلات پیش آمده است. فیلسوف بزرگ گفت که باید مثلثی را دید، آن وقت می توانیم فرض کنیم که مشکل دو سوم حل شده است.

فیثاغورث در مورد تدریس خود فقط به شاگردانش به صورت شفاهی و بدون هیچ یادداشتی و مخفی نگه داشتن آن صحبت کرد. متأسفانه آموزه های بزرگترین فیلسوف تا به امروز باقی نمانده است. برخی از آن به بیرون درز کرده است، اما نمی توان گفت که در آنچه شناخته شده است چقدر درست و چقدر نادرست است. حتی با وجود تاریخچه قضیه فیثاغورث، همه چیز قطعی نیست. مورخان ریاضیات در تألیف فیثاغورث تردید دارند، به نظر آنها، این قضیه قرن ها قبل از تولد او مورد استفاده قرار گرفت.

قضیه فیثاغورس

ممکن است عجیب به نظر برسد، اما هیچ واقعیت تاریخی برای اثبات قضیه توسط خود فیثاغورث وجود ندارد - نه در آرشیوها و نه در هیچ منبع دیگری. در نسخه مدرن، اعتقاد بر این است که به کسی جز خود اقلیدس تعلق ندارد.

شواهدی از یکی از بزرگترین مورخان ریاضیات، موریتز کانتور، وجود دارد که بر روی پاپیروسی که در موزه برلین ذخیره شده بود، کشف کرد که توسط مصریان در حدود 2300 سال قبل از میلاد نوشته شده بود. ه. برابری، که خوانده می شود: 3² + 4² = 5².

مختصری از تاریخ قضیه فیثاغورث

فرمول بندی قضیه از "آغاز" اقلیدسی در ترجمه مانند تفسیر مدرن به نظر می رسد. در قرائت آن چیز جدیدی وجود ندارد: مربع ضلع مقابل زاویه راست برابر است با مجموع مربعات اضلاع مجاور زاویه قائمه. این واقعیت که تمدن های باستانی هند و چین از این قضیه استفاده می کردند توسط رساله ژو بی سوان جین تأیید می شود. این شامل اطلاعاتی در مورد مثلث مصری است که نسبت تصویر را 3:4:5 توصیف می کند.

جالب نیست یکی دیگر از کتاب های ریاضی چینی "چو پی"، که همچنین از مثلث فیثاغورث با توضیح و نقشه هایی که منطبق با نقشه های هندسه هندویی بسخارا است، اشاره می کند. در مورد خود مثلث کتاب می گوید که اگر بتوان یک زاویه قائمه را به اجزای تشکیل دهنده آن تجزیه کرد، آنگاه خطی که انتهای اضلاع را به هم متصل می کند، اگر پایه سه و ارتفاع آن چهار باشد، برابر با پنج خواهد بود.

رساله هندی "Sulva Sutra" که قدمت آن به حدود قرن های 7-5 قبل از میلاد می رسد. e.، در مورد ساختن یک زاویه قائمه با استفاده از مثلث مصری می گوید.

اثبات قضیه

در قرون وسطی، دانش آموزان اثبات یک قضیه را بسیار دشوار می دانستند. دانش‌آموزان ضعیف قضایا را بدون اینکه معنی اثبات را بفهمند، از روی قلب یاد گرفتند. در این راستا، آنها لقب "خر" را دریافت کردند، زیرا قضیه فیثاغورث مانعی غیرقابل عبور برای آنها بود، مانند پلی برای الاغ. در قرون وسطی دانش آموزان آیه ای بازیگوش در مورد این قضیه می آوردند.

برای اثبات قضیه فیثاغورث به ساده‌ترین روش، باید اضلاع آن را بدون استفاده از مفهوم ناحیه‌ها در اثبات اندازه‌گیری کنید. طول ضلع مقابل زاویه راست c و a و b مجاور آن است، در نتیجه معادله a 2 + b 2 \u003d c 2 را به دست می آوریم. این جمله همانطور که در بالا ذکر شد با اندازه گیری طول اضلاع یک مثلث قائم الزاویه تأیید می شود.

اگر با در نظر گرفتن مساحت مستطیل های ساخته شده در اضلاع مثلث، اثبات قضیه را شروع کنیم، می توانیم مساحت کل شکل را تعیین کنیم. مساحت مربع با ضلع (a + b) و از طرفی مجموع مساحت چهار مثلث و مربع داخلی خواهد بود.

(a + b) 2 = 4 x ab/2 + c 2 ;

a 2 + 2ab + b 2 ;

c 2 = a 2 + b 2 که قرار بود ثابت شود.

اهمیت عملی قضیه فیثاغورث این است که می توان از آن برای یافتن طول قطعات بدون اندازه گیری آنها استفاده کرد. در طول ساخت سازه ها، فواصل، قرار دادن تکیه گاه ها و تیرها محاسبه می شود، مراکز ثقل تعیین می شود. قضیه فیثاغورث در تمام فناوری های مدرن نیز کاربرد دارد. آنها هنگام ایجاد فیلم در ابعاد 3D-6D قضیه را فراموش نکردند، جایی که علاوه بر 3 مقدار معمول: ارتفاع، طول، عرض، زمان، بو و طعم نیز در نظر گرفته می شود. می‌پرسید مزه‌ها و بوها چگونه با قضیه مرتبط هستند؟ همه چیز بسیار ساده است - هنگام نمایش یک فیلم، باید محاسبه کنید که کجا و چه بو و طعمی برای کارگردانی در سالن نمایش دهید.

این فقط آغاز است. دامنه بی حد و حصر برای کشف و ایجاد فناوری های جدید در انتظار ذهن های کنجکاو است.

فیثاغورث دانشمند یونانی است که حدود 2500 سال پیش (564-473 قبل از میلاد) می زیست.

یک مثلث قائم الزاویه داده شود که اضلاع آن آ, بو با(شکل 267).

بیایید در دو طرف آن مربع بسازیم. مساحت این مربع ها به ترتیب می باشد آ 2 , ب 2 و با 2. این را ثابت کنیم با 2 = a 2 +b 2 .

اجازه دهید دو مربع MKOR و M'K'O'R بسازیم (شکل 268، 269)، و برای ضلع هر یک از آنها قطعه ای برابر با مجموع پایه های مثلث قائم الزاویه ABC در نظر بگیریم.

پس از تکمیل ساخت و سازهای نشان داده شده در شکل های 268 و 269 در این مربع ها، خواهیم دید که مربع MKOR به دو مربع با مساحت تقسیم می شود. آ 2 و ب 2 و چهار مثلث قائم الزاویه که هر کدام برابر با مثلث قائم الزاویه ABC است. مربع M'K'O'R به یک چهار ضلعی (در شکل 269 سایه دار است) و چهار مثلث قائم الزاویه تقسیم می شود که هر یک از آنها نیز برابر با مثلث ABC است. چهارضلعی سایه دار یک مربع است، زیرا اضلاع آن مساوی است (هر کدام برابر است با افت مثلث ABC، یعنی. با) و زوایا خطوط مستقیم هستند ∠1 + ∠2 = 90 درجه، از این رو ∠3 = 90 درجه).

بنابراین، مجموع مساحت مربع های ساخته شده روی پایه ها (در شکل 268 این مربع ها سایه دار هستند) برابر است با مساحت مربع MKOR بدون مجموع مساحت های چهار مثلث مساوی و مساحت . مربع ساخته شده روی هیپوتانوس (در شکل 269 این مربع نیز سایه دار است) برابر با مساحت مربع M'K'O'R' برابر مربع MKOR است، بدون مجموع مساحت های چهار مثلث مشابه بنابراین، مساحت مربع ساخته شده بر روی فرضیه مثلث قائم الزاویه برابر است با مجموع مساحت مربع های ساخته شده بر روی پاها.

ما فرمول را دریافت می کنیم با 2 = a 2 +b 2، کجا با- هیپوتنوئوس، آو ب- پاهای یک مثلث قائم الزاویه

قضیه فیثاغورث را می توان به صورت زیر خلاصه کرد:

مجذور هیپوتانوس مثلث قائم الزاویه برابر است با مجموع مربع های پاها.

از فرمول با 2 = a 2 +b 2 می توانید فرمول های زیر را دریافت کنید:

آ 2 = با 2 - ب 2 ;

b 2 = با 2 - آ 2 .

از این فرمول ها می توان برای یافتن ضلع مجهول مثلث قائم الزاویه با توجه به دو ضلع آن استفاده کرد.

مثلا:

الف) اگر پا داده شود آ= 4 سانتی متر، ب\u003d 3 سانتی متر، سپس می توانید هیپوتانوس را پیدا کنید ( با):

با 2 = a 2 +b 2، یعنی با 2 = 4 2 + 3 2 ; با 2 = 25، از آنجا با= √25 = 5 (سانتی متر)؛

ب) اگر هیپوتانوز داده شود با= 17 سانتی متر و پا آ= 8 سانتی متر، سپس می توانید یک پای دیگر پیدا کنید ( ب):

ب 2 = با 2 - آ 2، یعنی ب 2 = 17 2 - 8 2 ; ب 2 = 225، از آنجا ب= √225 = 15 (سانتی متر).

نتیجه: اگر در دو مثلث قائم الزاویه ABC و A 1 B 1 C 1 هیپوتانوز باشد باو با 1 برابر هستند و ساق بمثلث ABC بزرگتر از ساق است ب 1 مثلث A 1 B 1 C 1,

سپس پا آمثلث ABC کمتر از ساق است آ 1 مثلث A 1 B 1 C 1 .

در واقع، بر اساس قضیه فیثاغورث، به دست می آوریم:

آ 2 = با 2 - ب 2 ,

آ 1 2 = با 1 2 - ب 1 2

در فرمول های نوشته شده، مینیوندها با هم برابرند، و فرعی در فرمول اول بزرگتر از فرعی در فرمول دوم است، بنابراین، تفاوت اول کمتر از دومی است.

یعنی آ 2 a 1 2 . جایی که آیک 1.

1

شاپووالوا L.A. (ایستگاه Egorlykskaya، MBOU ESOSH شماره 11)

1. گلیزر جی.آی. تاریخچه ریاضیات در مدرسه هفتم - کلاس هشتم، راهنمای معلمان، - M: آموزش و پرورش، 1982.

2. Dempan I.Ya.، Vilenkin N.Ya. کتاب «پشت صفحات کتاب ریاضی» برای دانش آموزان پایه پنجم تا ششم. - م.: روشنگری، 1989.

3. Zenkevich I.G. "زیبایی شناسی درس ریاضی". - م.: روشنگری، 1981.

4. لیتزمن V. قضیه فیثاغورث. - م.، 1960.

5. Voloshinov A.V. "فیثاغورث". - م.، 1993.

6. Pichurin L.F. "فراتر از صفحات یک کتاب درسی جبر". - م.، 1990.

7. Zemlyakov A.N. "هندسه در پایه دهم." - م.، 1986.

8. روزنامه «ریاضیات» 17/96.

9. روزنامه «ریاضیات» 3/1376.

10. Antonov N.P.، Vygodskii M.Ya.، Nikitin V.V.، Sankin A.I. «مجموعه مسائل ریاضی ابتدایی». - م.، 1963.

11. Dorofeev G.V.، Potapov M.K.، Rozov N.Kh. "راهنمای ریاضیات". - م.، 1973.

12. Shchetnikov A.I. "آموزه فیثاغورث در مورد عدد و قدر". - نووسیبیرسک، 1997.

13. «اعداد واقعی. عبارات غیرمنطقی» پایه هشتم. انتشارات دانشگاه تومسک. - تامسک، 1997.

14. آتاناسیان م.س. "هندسه" پایه 7-9. - م.: روشنگری، 1991.

15. آدرس اینترنتی: www.moypifagor.narod.ru/

16. آدرس اینترنتی: http://www.zaitseva-irina.ru/html/f1103454849.html.

در این سال تحصیلی، من با یک قضیه جالب آشنا شدم، همانطور که معلوم شد، از زمان های قدیم شناخته شده است:

"مربع ساخته شده بر روی فرضیه مثلث قائم الزاویه برابر است با مجموع مربع های ساخته شده بر روی پاها."

معمولاً کشف این گفته به فیثاغورث فیلسوف و ریاضیدان یونان باستان (قرن ششم قبل از میلاد) نسبت داده می شود. اما مطالعه نسخه های خطی قدیمی نشان داد که این گفته مدت ها قبل از تولد فیثاغورث شناخته شده بود.

تعجب کردم که چرا در این مورد با نام فیثاغورث همراه است.

ارتباط موضوع: قضیه فیثاغورث از اهمیت زیادی برخوردار است: در هندسه به معنای واقعی کلمه در هر مرحله استفاده می شود. من معتقدم که آثار فیثاغورث هنوز هم مرتبط هستند، زیرا به هر کجا که نگاه کنیم، همه جا می‌توانیم ثمرات ایده‌های بزرگ او را ببینیم که در شاخه‌های مختلف زندگی مدرن تجسم یافته است.

هدف از تحقیق من این بود که بفهمم فیثاغورث کیست و چه رابطه ای با این قضیه دارد.

با مطالعه تاریخچه قضیه، تصمیم گرفتم بفهمم:

آیا دلایل دیگری برای این قضیه وجود دارد؟

اهمیت این قضیه در زندگی مردم چیست؟

فیثاغورث چه نقشی در توسعه ریاضیات داشت؟

از زندگی نامه فیثاغورث

فیثاغورث ساموسی دانشمند بزرگ یونانی است. شهرت آن با نام قضیه فیثاغورث مرتبط است. اگرچه اکنون می دانیم که این قضیه در بابل باستان 1200 سال قبل از فیثاغورث شناخته شده بود و در مصر 2000 سال قبل از او یک مثلث قائم الزاویه با ضلع های 3، 4، 5 شناخته شده بود، ما هنوز آن را به نام این باستان می نامیم. دانشمند

تقریباً هیچ چیز به طور قطعی در مورد زندگی فیثاغورث شناخته شده نیست، اما تعداد زیادی افسانه با نام او مرتبط است.

فیثاغورث در سال 570 قبل از میلاد در جزیره ساموس به دنیا آمد.

فیثاغورث ظاهری زیبا داشت، ریش بلندی بر سر داشت و بر سرش سنگی طلایی داشت. فیثاغورث یک نام نیست، بلکه لقبی است که فیلسوف به دلیل اینکه همیشه به درستی و متقاعد کننده صحبت می کند، مانند یک اوراکل یونانی دریافت کرده است. (فیثاغورث - "گفتار متقاعد کننده").

در سال 550 قبل از میلاد فیثاغورث تصمیم می گیرد و به مصر می رود. بنابراین، یک کشور ناشناخته و یک فرهنگ ناشناخته در برابر فیثاغورس باز می شود. فیثاغورث در این کشور بسیار شگفت زده و شگفت زده شد و پس از برخی مشاهدات از زندگی مصریان، فیثاغورث متوجه شد که مسیر دانش، که توسط کاست کاهنان محافظت می شود، از طریق دین می گذرد.

فیثاغورث پس از یازده سال تحصیل در مصر به سرزمین مادری خود می رود و در طول مسیر به اسارت بابلی ها می افتد. در آنجا با علم بابلی آشنا می شود که بیشتر از علم مصر توسعه یافته بود. بابلی ها می دانستند که چگونه معادلات خطی، درجه دوم و برخی از انواع معادلات مکعبی را حل کنند. پس از فرار از اسارت، به دلیل فضای خشونت و ظلم حاکم بر آنجا، نتوانست مدت زیادی در وطن بماند. او تصمیم گرفت به کروتون (یک مستعمره یونانی در شمال ایتالیا) نقل مکان کند.

در کروتون است که باشکوه ترین دوره زندگی فیثاغورث آغاز می شود. او در آنجا چیزی شبیه یک برادری مذهبی-اخلاقی یا یک رهبانی مخفی ایجاد کرد که اعضای آن موظف بودند به اصطلاح زندگی فیثاغورثی را رهبری کنند.

فیثاغورث و فیثاغورثی ها

فیثاغورث در یک مستعمره یونانی در جنوب شبه جزیره آپنین یک برادری مذهبی و اخلاقی مانند یک رهبانی تشکیل داد که بعداً اتحادیه فیثاغورث نامیده شد. اعضای اتحادیه باید اصول خاصی را رعایت می کردند: اولاً تلاش برای زیبایی و شکوه، ثانیاً مفید بودن و ثالثاً تلاش برای لذت عالی.

سیستم قواعد اخلاقی و اخلاقی که فیثاغورث به شاگردانش وصیت کرده بود، در نوعی کد اخلاقی فیثاغورثی "آیات طلایی" که در دوران باستان، قرون وسطی و رنسانس بسیار محبوب بود، جمع آوری شد.

نظام مطالعات فیثاغورث شامل سه بخش بود:

آموزش اعداد - حساب،

آموزش در مورد اشکال - هندسه،

آموزه هایی در مورد ساختار جهان - نجوم.

سیستم آموزشی که توسط فیثاغورث وضع شده بود قرن ها ادامه داشت.

مکتب فیثاغورث برای دادن ویژگی علم به هندسه بسیار تلاش کرد. ویژگی اصلی روش فیثاغورثی ترکیب هندسه با حساب بود.

فیثاغورث بسیار به نسبت ها و پیشرفت ها و احتمالاً به شباهت شکل ها پرداخته است، زیرا به او اعتبار حل این مشکل داده می شود: «بر اساس با توجه به دو رقم."

فیثاغورث و شاگردانش مفهوم چند ضلعی، دوستانه، اعداد کامل را معرفی کردند و خواص آنها را مورد مطالعه قرار دادند. حساب، به عنوان یک عمل محاسبه، فیثاغورث را مورد توجه قرار نداد و او با افتخار اعلام کرد که "حساب را بر منافع تاجر ترجیح می دهد."

اعضای اتحادیه فیثاغورث ساکنان بسیاری از شهرهای یونان بودند.

فیثاغورثی ها نیز زنان را در جامعه خود می پذیرفتند. اتحادیه بیش از بیست سال شکوفا شد و سپس آزار و اذیت اعضای آن آغاز شد و بسیاری از دانشجویان کشته شدند.

در مورد مرگ خود فیثاغورث افسانه های مختلفی وجود داشت. اما آموزه های فیثاغورث و شاگردانش به حیات خود ادامه دادند.

از تاریخچه ایجاد قضیه فیثاغورث

در حال حاضر مشخص است که این قضیه توسط فیثاغورث کشف نشده است. با این حال، برخی معتقدند که این فیثاغورث بود که اولین بار اثبات کامل آن را ارائه کرد، در حالی که برخی دیگر این شایستگی را رد کردند. برخی برهانی را که اقلیدس در اولین کتاب از عناصر خود آورده است به فیثاغورث نسبت می دهند. از سوی دیگر، پروکلوس مدعی است که اثبات در عناصر به خاطر خود اقلیدس است. همانطور که می بینیم، تاریخ ریاضیات تقریباً هیچ داده عینی قابل اعتمادی در مورد زندگی فیثاغورث و فعالیت های ریاضی او ندارد.

بیایید بررسی تاریخی خود را از قضیه فیثاغورث با چین باستان شروع کنیم. در اینجا کتاب ریاضی چوپی توجه ویژه ای را به خود جلب می کند. این مقاله در مورد مثلث فیثاغورث با ضلع های 3، 4 و 5 چنین می گوید:

"اگر یک زاویه قائمه به اجزای تشکیل دهنده آن تجزیه شود، خطی که انتهای اضلاع آن را به هم متصل می کند، زمانی که پایه 3 و ارتفاع آن 4 باشد، 5 خواهد بود."

بازتولید روش ساخت آنها بسیار آسان است. یک طناب به طول 12 متر بردارید و در امتداد یک نوار رنگی به فاصله 3 متر به آن ببندید. از یک سر و 4 متر از سر دیگر. یک زاویه قائم بین اضلاع به طول 3 و 4 متر محصور خواهد شد.

هندسه در میان هندوها ارتباط نزدیکی با این آیین داشت. بسیار محتمل است که قضیه مربع هیپوتنوس قبلاً در قرن هشتم قبل از میلاد در هند شناخته شده بود. در کنار نسخه های صرفاً آیینی، آثاری با ماهیت هندسی الهیاتی وجود دارد. در این نوشته ها که قدمت آن به قرن چهارم یا پنجم قبل از میلاد می رسد، با ساختن یک زاویه قائمه با استفاده از مثلث با اضلاع 15، 36، 39 مواجه می شویم.

در قرون وسطی، قضیه فیثاغورث حد و مرز، اگر نه از بزرگترین ممکن، حداقل دانش ریاضی خوب را تعریف کرد. ترسیم مشخصه قضیه فیثاغورث، که اکنون گاهی اوقات توسط دانش آموزان مدرسه تبدیل می شود، به عنوان مثال، به کلاه بالایی که لباس یک استاد یا یک مرد می پوشد، اغلب در آن روزها به عنوان نماد ریاضیات استفاده می شد.

در پایان، ما فرمول‌های مختلفی از قضیه فیثاغورث را ارائه می‌کنیم که از یونانی، لاتین و آلمانی ترجمه شده‌اند.

قضیه اقلیدس می گوید (ترجمه تحت اللفظی):

"در مثلث قائم الزاویه، مربع ضلعی که زاویه سمت راست را در بر می گیرد برابر است با مربع های اضلاع که زاویه قائمه را در بر می گیرند."

همانطور که می بینید، در کشورهای مختلف و زبان های مختلف نسخه های مختلفی از فرمول بندی قضیه آشنا وجود دارد. آنها که در زمان‌های مختلف و به زبان‌های مختلف ایجاد شده‌اند، جوهر یک الگوی ریاضی را منعکس می‌کنند که اثبات آن نیز چندین گزینه دارد.

پنج راه برای اثبات قضیه فیثاغورث

اثبات چینی باستان

در یک طراحی چینی باستان، چهار مثلث قائم الزاویه مساوی با پایه‌های a، b و فرضیه c روی هم چیده شده‌اند به طوری که خط بیرونی آن‌ها مربعی با ضلع a + b و درونی مربعی با ضلع c را تشکیل می‌دهد. هیپوتنوئوس

a2 + 2ab + b2 = c2 + 2ab

اثبات توسط جی.گاردفیلد (1882)

اجازه دهید دو مثلث قائم الزاویه مساوی ترتیب دهیم تا ساق یکی از آنها ادامه دیگری باشد.

مساحت ذوزنقه مورد نظر حاصل ضرب نصف مجموع قاعده ها و ارتفاع است.

از طرف دیگر، مساحت ذوزنقه برابر است با مجموع مساحت مثلث های حاصل:

با معادل سازی این عبارات، دریافت می کنیم:

اثبات ساده است

این اثبات در ساده ترین حالت مثلث قائم الزاویه متساوی الساقین به دست می آید.

احتمالاً قضیه با او شروع شد.

در واقع، فقط باید به کاشی کاری مثلث های قائم الزاویه متساوی الساقین نگاه کرد تا متوجه شد که این قضیه درست است.

به عنوان مثال، برای مثلث ABC: مربع ساخته شده روی فرضیه AC شامل 4 مثلث اولیه و مربع های ساخته شده روی پاها شامل دو مثلث است. قضیه ثابت شده است.

اثبات هندوهای باستان

مربع با ضلع (a + b) را می توان به قسمت هایی مانند شکل 1 تقسیم کرد. 12. a، یا همانطور که در شکل. 12 ب. واضح است که قسمت های 1، 2، 3، 4 در هر دو شکل یکسان است. و اگر مساوی از مساوات کم شود، مساوی باقی می ماند، یعنی. c2 = a2 + b2.

برهان اقلیدس

برای دو هزار سال، متداول ترین آنها اثبات قضیه فیثاغورث بود که توسط اقلیدس ابداع شد. در کتاب معروف او «آغاز» آمده است.

اقلیدس ارتفاع BH را از راس زاویه قائم به هیپوتانوس پایین آورد و ثابت کرد که امتداد آن مربع تکمیل شده روی هیپوتنوس را به دو مستطیل تقسیم می کند که مساحت آنها برابر است با مساحت مربع های مربوطه ساخته شده روی پاها.

رسم مورد استفاده در اثبات این قضیه را به شوخی «شلوار فیثاغورثی» می نامند. او برای مدت طولانی یکی از نمادهای علوم ریاضی به حساب می آمد.

کاربرد قضیه فیثاغورث

اهمیت قضیه فیثاغورث در این است که بیشتر قضایای هندسه را می توان از آن استخراج کرد و یا به کمک آن بسیاری از مسائل را حل کرد. علاوه بر این، اهمیت عملی قضیه فیثاغورث و قضیه معکوس آن در این است که می توان از آنها برای یافتن طول پاره ها بدون اندازه گیری خود پاره ها استفاده کرد. این، همانطور که بود، راه را از یک خط مستقیم به یک صفحه، از یک صفحه به فضای حجمی و فراتر از آن باز می کند. به همین دلیل است که قضیه فیثاغورث برای بشریت که به دنبال کشف ابعاد بیشتر و ایجاد فناوری در این ابعاد است، بسیار مهم است.

نتیجه

قضیه فیثاغورث آنقدر معروف است که تصور کسی که در مورد آن نشنیده باشد دشوار است. فهمیدم که چندین راه برای اثبات قضیه فیثاغورث وجود دارد. من تعدادی از منابع تاریخی و ریاضی از جمله اطلاعات موجود در اینترنت را مطالعه کردم و متوجه شدم که قضیه فیثاغورث نه تنها به دلیل تاریخچه آن، بلکه به دلیل اینکه جایگاه مهمی در زندگی و علم دارد جالب است. این را تفاسیر مختلفی از متن این قضیه در این نوشتار و راه های اثبات آن ارائه کردم.

پس قضیه فیثاغورث یکی از اصلی ترین و شاید بتوان گفت مهم ترین قضیه هندسه است. اهمیت آن در این است که بیشتر قضایای هندسه را می توان از آن یا به کمک آن استنباط کرد. قضیه فیثاغورث نیز از این جهت قابل توجه است که به خودی خود اصلاً آشکار نیست. به عنوان مثال، ویژگی های یک مثلث متساوی الساقین را می توان مستقیماً در نقاشی مشاهده کرد. اما مهم نیست که چقدر به یک مثلث قائم الزاویه نگاه کنید، هرگز نمی بینید که یک رابطه ساده بین اضلاع آن وجود دارد: c2 = a2 + b2. بنابراین، تجسم اغلب برای اثبات آن استفاده می شود. شایستگی فیثاغورث این بود که اثبات علمی کاملی برای این قضیه ارائه کرد. شخصیت خود دانشمند که به طور تصادفی با این قضیه حافظه اش حفظ نمی شود، جالب است. فیثاغورث یک سخنران، معلم و مربی فوق العاده است، سازمان دهنده مدرسه خود، با تمرکز بر هماهنگی موسیقی و اعداد، خوبی و عدالت، دانش و سبک زندگی سالم. او ممکن است به عنوان نمونه ای برای ما، نوادگان دور، باشد.

پیوند کتابشناختی

Tumanova S.V. چندین راه برای اثبات قضیه فیثاغورث // در علم شروع کنید. - 1395. - شماره 2. - ص 91-95;
URL: http://science-start.ru/ru/article/view?id=44 (تاریخ دسترسی: 2020/02/28).

به گفته van der Waerden، به احتمال بسیار زیاد این نسبت به شکل کلی قبلاً در قرن 18 قبل از میلاد در بابل شناخته شده بود. ه.

تقریباً 400 سال قبل از میلاد ه.، طبق گفته پروکلوس، افلاطون روشی را برای یافتن سه گانه فیثاغورثی، ترکیب جبر و هندسه ارائه کرد. حدود 300 پ.م. ه. در «عناصر» اقلیدس قدیمی‌ترین برهان بدیهی قضیه فیثاغورث ظاهر شد.

جمله بندی

فرمول اصلی شامل عملیات جبری است - در یک مثلث قائم الزاویه که طول پاهای آن برابر است. a (\displaystyle a)و b (\displaystyle b)، و طول هیپوتانوس است c (\displaystyle c)، رابطه محقق می شود:

.

یک فرمول هندسی معادل نیز امکان پذیر است، با توسل به مفهوم مساحت - شکل: در یک مثلث قائم الزاویه، مساحت مربع ساخته شده روی هیپوتنوس برابر با مجموع مساحت مربع های ساخته شده روی پاها است. در این شکل، قضیه در اصل اقلیدس فرموله شده است.

قضیه فیثاغورث معکوس- عبارت در مورد مستطیل بودن هر مثلثی که طول اضلاع آن با رابطه مرتبط است. a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). در نتیجه، برای هر سه اعداد مثبت a (\displaystyle a), b (\displaystyle b)و c (\displaystyle c)، به طوری که a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2))، یک مثلث قائم الزاویه با پاها وجود دارد a (\displaystyle a)و b (\displaystyle b)و هیپوتانوز c (\displaystyle c).

اثبات

حداقل 400 اثبات قضیه فیثاغورث در ادبیات علمی ثبت شده است که هم با ارزش اساسی هندسه و هم با ماهیت ابتدایی نتیجه توضیح داده شده است. جهت‌های اصلی اثبات عبارتند از: استفاده جبری از نسبت‌های عناصر به مثلث (مثلاً روش تشابه رایج است)، روش مساحت، همچنین اثبات‌های عجیب و غریب مختلفی وجود دارد (مثلاً با استفاده از معادلات دیفرانسیل).

از طریق مثلث های مشابه

برهان کلاسیک اقلیدس با هدف ایجاد برابری مساحت‌های بین مستطیل‌هایی است که با تشریح مربع بالای هیپوتنوس با ارتفاع از زاویه راست با مربع‌های بالای پاها تشکیل شده‌اند.

ساختار مورد استفاده برای اثبات به شرح زیر است: برای یک مثلث قائم الزاویه با زاویه قائمه C (\displaystyle C)، مربع روی پاها و و مربع روی هیپوتنوز A B I K (\displaystyle ABIK)ارتفاع در حال ساخت است C H (\displaystyle CH)و پرتویی که آن را ادامه می دهد s (\displaystyle s)، مربع بالای هیپوتانوس را به دو مستطیل تقسیم می کنیم و . هدف اثبات برابری مساحت های مستطیل است A H J K (\displaystyle AHJK)با مربع روی ساق A C (\displaystyle AC); مساوی مساحت های مستطیل دوم که یک مربع بالای هیپوتنوز است و مستطیل بالای پایه دیگر به همین ترتیب برقرار می شود.

تساوی مساحت های یک مستطیل A H J K (\displaystyle AHJK)و A C E D (\displaystyle ACED)از طریق همخوانی مثلث ها ایجاد می شود △ A C K ​​(\displaystyle \ مثلث ACK)و △ A B D (\displaystyle \مثلث ABD)که مساحت هر کدام برابر با نصف مساحت مربع است A H J K (\displaystyle AHJK)و A C E D (\displaystyle ACED)به ترتیب در رابطه با خاصیت زیر: مساحت مثلث برابر با نصف مساحت مستطیل در صورتی است که شکل ها دارای ضلع مشترک باشند و ارتفاع مثلث تا ضلع مشترک ضلع دیگر باشد. مستطیل همخوانی مثلث ها از برابری دو ضلع (اضلاع مربع ها) و زاویه بین آنها (متشکل از یک زاویه قائمه و یک زاویه در A (\displaystyle A).

بنابراین، اثبات ثابت می کند که مساحت مربع بالای هیپوتانوس، متشکل از مستطیل ها A H J K (\displaystyle AHJK)و B H J I (\displaystyle BHJI)، برابر است با مجموع مساحت مربع های بالای پاها.

اثبات لئوناردو داوینچی

روش منطقه همچنین شامل اثبات یافت شده توسط لئوناردو داوینچی است. بگذارید یک مثلث قائم الزاویه وجود داشته باشد △ A B C (\displaystyle \مثلث ABC)زاویه راست C (\displaystyle C)و مربع ها A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG)و A B H J (\displaystyle ABHJ)(تصویر را ببینید). در این اثبات در کنار H J (\displaystyle HJ)دومی، یک مثلث به بیرون ساخته شده است، همخوان △ A B C (\displaystyle \مثلث ABC)علاوه بر این، هم نسبت به هیپوتانوس و هم نسبت به ارتفاع آن منعکس می شود (یعنی J I = B C (\displaystyle JI=BC)و H I = A C (\displaystyle HI=AC)). سر راست C I (\displaystyle CI)مربع ساخته شده روی هیپوتنوس را به دو قسمت مساوی تقسیم می کند، زیرا مثلث است △ A B C (\displaystyle \مثلث ABC)و △ J H I (\displaystyle \مثلث JHI)در ساخت و ساز برابر هستند. برهان همخوانی چهار ضلعی را ثابت می کند C A J I (\displaystyle CAJI)و D A B G (\displaystyle DABG)که مساحت هر کدام از یک طرف برابر است با مجموع نصف مساحت مربع های روی پاها و مساحت مثلث اصلی از طرف دیگر نصف مساحت مربع روی هیپوتانوس به اضافه مساحت مثلث اصلی. در مجموع، نیمی از مجموع مساحت مربع های روی پاها برابر است با نصف مساحت مربع روی هیپوتانوس، که معادل فرمول هندسی قضیه فیثاغورث است.

اثبات با روش بینهایت کوچک

چندین اثبات با استفاده از تکنیک معادلات دیفرانسیل وجود دارد. به طور خاص، هاردی با استفاده از افزایش بی نهایت کوچک پا به اثبات رسیده است a (\displaystyle a)و b (\displaystyle b)و هیپوتانوز c (\displaystyle c)و حفظ شباهت با مستطیل اصلی، یعنی اطمینان از تحقق روابط دیفرانسیل زیر:

d a d c = c a (\displaystyle (\frac (da)(dc))=(\frac (c)(a))), d b d c = c b (\displaystyle (\frac (db)(dc))=(\frac (c)(b))).

با روش تفکیک متغیرها، یک معادله دیفرانسیل از آنها استخراج می شود c d c = a d a + b d b (\displaystyle c\ dc=a\,da+b\,db)، که ادغام آن رابطه را می دهد c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). اعمال شرایط اولیه a = b = c = 0 (\displaystyle a=b=c=0)یک ثابت را 0 تعریف می کند که منجر به اثبات قضیه می شود.

وابستگی درجه دوم در فرمول نهایی به دلیل تناسب خطی بین اضلاع مثلث و افزایش ها ظاهر می شود، در حالی که مجموع به دلیل مشارکت مستقل از افزایش پایه های مختلف است.

تغییرات و تعمیم

اشکال هندسی مشابه در سه طرف

یک تعمیم هندسی مهم قضیه فیثاغورث توسط اقلیدس در "آغاز" ارائه شد، که از مساحت مربع ها در اضلاع به مناطق اشکال هندسی مشابه دلخواه حرکت می کند: مجموع مساحت های چنین اشکالی که روی پاها ساخته شده اند خواهد بود. برابر با مساحت شکلی شبیه به آنها که بر روی هیپوتانوس ساخته شده است.

ایده اصلی این تعمیم این است که مساحت چنین شکل هندسی با مربع هر یک از ابعاد خطی آن و به ویژه با مربع طول هر ضلع متناسب است. بنابراین، برای ارقام مشابه با مناطق A (\displaystyle A), B (\displaystyle B)و C (\displaystyle C)ساخته شده بر روی پاهای با طول a (\displaystyle a)و b (\displaystyle b)و هیپوتانوز c (\displaystyle c)بر این اساس، یک رابطه وجود دارد:

A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (\displaystyle (\frac (A)(a^(2)))=(\frac (B )(b^(2)))=(\frac (C)(c^(2)))\,\arrow \,A+B=(\frac (a^(2))(c^(2) ))C+(\frac (b^(2))(c^(2)))C).

از آنجایی که طبق قضیه فیثاغورث a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2))، سپس انجام می شود.

به علاوه، اگر بتوان بدون توسل به قضیه فیثاغورث ثابت کرد که برای مساحت های سه شکل هندسی مشابه در اضلاع یک مثلث قائم الزاویه، رابطه A + B = C (\displaystyle A+B=C)، سپس با استفاده از معکوس اثبات تعمیم اقلیدس، می توانیم اثبات قضیه فیثاغورث را استخراج کنیم. به عنوان مثال، اگر روی هیپوتانوس یک مثلث قائم الزاویه همخوان با مساحت اولیه بسازیم C (\displaystyle C)، و روی پاها - دو مثلث قائم الزاویه مشابه با مناطق A (\displaystyle A)و B (\displaystyle B)، سپس معلوم می شود که مثلث های روی پاها در نتیجه تقسیم مثلث اولیه بر ارتفاع آن تشکیل می شوند ، یعنی مجموع دو ناحیه کوچکتر از مثلث ها برابر با مساحت مثلث سوم است ، بنابراین A + B = C (\displaystyle A+B=C)و با اعمال رابطه برای اشکال مشابه، قضیه فیثاغورث به دست می آید.

قضیه کسینوس

قضیه فیثاغورث یک مورد خاص از قضیه کسینوس عمومی تر است که طول اضلاع را در یک مثلث دلخواه به هم مرتبط می کند:

a 2 + b 2 − 2 a b cos ⁡ θ = c 2 (\displaystyle a^(2)+b^(2)-2ab\cos (\theta)=c^(2)),

زاویه بین اضلاع کجاست a (\displaystyle a)و b (\displaystyle b). اگر زاویه 90 درجه باشد، پس cos ⁡ θ = 0 (\displaystyle \cos \theta =0)، و فرمول به قضیه فیثاغورث معمولی ساده می شود.

مثلث دلخواه

یک تعمیم از قضیه فیثاغورث به یک مثلث دلخواه وجود دارد که صرفاً بر اساس نسبت طول اضلاع عمل می کند، اعتقاد بر این است که اولین بار توسط ستاره شناس Sabian Sabit-ibn-Kurra ایجاد شد. در آن، برای یک مثلث دلخواه با اضلاع، یک مثلث متساوی الساقین با پایه در ضلع c (\displaystyle c)، راس منطبق با راس مثلث اصلی، مقابل ضلع c (\displaystyle c)و زوایای قاعده برابر با زاویه θ (\displaystyle \theta)طرف مقابل c (\displaystyle c). در نتیجه، دو مثلث شبیه به مثلث اصلی تشکیل می شود: اولی با اضلاع a (\displaystyle a)، ضلع جانبی مثلث متساوی الساقین محاطی دور از آن و r (\displaystyle r)- قطعات جانبی c (\displaystyle c); دومی از طرف با آن متقارن است b (\displaystyle b)با یک مهمانی s (\displaystyle s)- قسمت مربوطه طرف c (\displaystyle c). در نتیجه، رابطه برآورده می شود:

a 2 + b 2 = c (r + s) (\displaystyle a^(2)+b^(2)=c(r+s)),

که به قضیه فیثاغورث در θ = π / 2 (\displaystyle \theta =\pi /2). این نسبت نتیجه شباهت مثلث های تشکیل شده است:

c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (\displaystyle (\frac (c)(a))=(\frac (a)(r)),\,(\frac (c) (ب))=(\frac (b)(s))\،\راست فلش \,cr+cs=a^(2)+b^(2)).

قضیه ناحیه پاپوس

هندسه نااقلیدسی

قضیه فیثاغورث از بدیهیات هندسه اقلیدسی مشتق شده است و برای هندسه غیراقلیدسی نامعتبر است - تحقق قضیه فیثاغورث مساوی است با فرض توازی اقلیدسی.

در هندسه غیر اقلیدسی، رابطه بین اضلاع یک مثلث قائم الزاویه لزوماً به شکلی متفاوت از قضیه فیثاغورث خواهد بود. به عنوان مثال، در هندسه کروی، هر سه ضلع مثلث قائم الزاویه که یک اکتانت از یک واحد کره را محدود می کند، طول دارند. π / 2 (\displaystyle \pi /2)، که با قضیه فیثاغورث در تضاد است.

علاوه بر این، قضیه فیثاغورث در هندسه هذلولی و بیضوی معتبر است، اگر شرط مستطیل بودن مثلث با شرطی جایگزین شود که مجموع دو زاویه مثلث باید برابر با زاویه سوم باشد.

هندسه کروی

برای هر مثلث قائم الزاویه روی کره ای با شعاع R (\displaystyle R)(مثلاً اگر زاویه در مثلث قائم باشد) با اضلاع a , b , c (\displaystyle a,b,c)رابطه بین طرفین عبارت است از:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) (\displaystyle \cos \left((\frac (c)(R))\right)=\cos \left((\frac (a)(R))\راست)\cdot \cos \left((\frac (b)(R))\راست)).

این برابری را می توان به عنوان یک مورد خاص از قضیه کسینوس کروی استخراج کرد که برای همه مثلث های کروی معتبر است:

cos ⁡ (c R) = cos ⁡ (a R) ⋅ cos ⁡ (b R) + sin ⁡ (a R) ⋅ sin⁡ (b R) ⋅ cos ⁡ γ (\displaystyle \cos \left((\frac ( c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac (b)(R))\right)\cdot \cos \gamma). ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b),

جایی که ch (\displaystyle \operatorname (ch))- هذلولی-کوزین. این فرمول یک مورد خاص از قضیه کسینوس هذلولی است که برای همه مثلث ها معتبر است:

ch ⁡ c = ch ⁡ a ⋅ ch ⁡ b − sh ⁡ a ⋅ sh ⁡ b ⋅ cos ⁡ γ (\displaystyle \operatorname (ch) c=\operatorname (ch) a\cdot \operatorname (ch) b-\operatorname (sh) a\cdot \operatorname (sh) b\cdot \cos \gamma),

جایی که γ (\displaystyle \gamma)- زاویه ای که راس آن مخالف یک ضلع است c (\displaystyle c).

استفاده از سری تیلور برای کسینوس هذلولی ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\حدود 1+x^(2)/2)) می توان نشان داد که اگر مثلث هذلولی کاهش یابد (یعنی چه زمانی a (\displaystyle a), b (\displaystyle b)و c (\displaystyle c)تمایل به صفر دارند)، سپس روابط هذلولی در یک مثلث قائم الزاویه به رابطه قضیه کلاسیک فیثاغورث نزدیک می شود.

کاربرد

فاصله در سیستم های مستطیلی دو بعدی

مهمترین کاربرد قضیه فیثاغورث تعیین فاصله بین دو نقطه در یک سیستم مستطیلی مختصات است: فاصله. s (\displaystyle s)بین نقاط با مختصات (a, b) (\displaystyle (a,b))و (c , d) (\displaystyle (c,d))برابر است با:

s = (a - c) 2 + (b - d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).

برای اعداد مختلط، قضیه فیثاغورث یک فرمول طبیعی برای یافتن عدد مختلط مدول - برای z = x + y i (\displaystyle z=x+yi)برابر است با طول