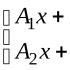Właściwości układów kwantowych. Układy kwantowe i ich właściwości
Poziomy energii (atomowe, molekularne, jądrowe)
1. Charakterystyka stanu układu kwantowego
2. Poziomy energetyczne atomów
3. Poziomy energetyczne cząsteczek
4. Poziomy energetyczne jąder
Charakterystyka stanu układu kwantowego
Podstawa wyjaśnienia właściwości atomów, cząsteczek i jąder atomowych, tj. zjawiska zachodzące w elementach objętościowych o skalach liniowych 10 -6 -10 -13 cm leżą w obszarze mechaniki kwantowej. Według mechaniki kwantowej każdy układ kwantowy (tj. układ mikrocząstek przestrzegający praw kwantowych) charakteryzuje się pewnym zbiorem stanów. Ogólnie rzecz biorąc, ten zbiór stanów może być dyskretny (dyskretne widmo stanów) lub ciągły (ciągłe widmo stanów). Charakterystyka stanu izolowanego układu zjawisk. energia wewnętrzna układu (zwana dalej po prostu energią), całkowity moment pędu (MCM) i parzystość.
Energia układu.
Układ kwantowy, będąc w różnych stanach, ma, ogólnie rzecz biorąc, różne energie. Energia połączonego systemu może przyjmować dowolną wartość. Ten zbiór możliwych wartości energii nazywa się. dyskretne widmo energii i mówi się, że energia jest skwantowana. Przykładem może być energia. widmo atomu (patrz poniżej). Niezwiązany układ oddziałujących cząstek ma ciągłe widmo energii, a energia może przyjmować dowolne wartości. Przykładem takiego systemu jest wolny elektron (E) w polu kulombowskim jądra atomowego. Ciągłe widmo energii można przedstawić jako zbiór nieskończenie dużej liczby dyskretnych stanów, pomiędzy którymi znajduje się energia. luki są nieskończenie małe.
Stan, któremu odpowiada najniższa możliwa energia dla danego układu, nazywa się. main: wywoływane są wszystkie pozostałe stany. podekscytowany. Często wygodnie jest zastosować konwencjonalną skalę energetyczną, w której głównie występuje energia stan uważa się za punkt wyjścia, tj. przyjmuje się, że jest równa zeru (w tej konwencjonalnej skali energia jest oznaczona literą mi). Jeśli system jest w stanie N(i indeks N=1 jest przypisane do głównego. stan), ma energię En, to mówią, że system jest na poziomie energetycznym En. Numer N, o numerze UE, tzw. Liczba kwantowa. Ogólnie rzecz biorąc, każde U.e. można scharakteryzować nie jedną liczbą kwantową, ale ich kombinacją; następnie indeksuj N oznacza całość tych liczb kwantowych.
Jeśli warunki nr 1, nr 2, n 3,..., n k odpowiada tej samej energii, tj. jeden UE, wtedy ten poziom nazywa się zdegenerowanym i liczbą k- wielość zwyrodnień.
Podczas wszelkich przemian układu zamkniętego (a także układu znajdującego się w stałym polu zewnętrznym) jego energia całkowita pozostaje niezmieniona. Dlatego energia odnosi się do tzw. zachowane wartości. Prawo zachowania energii wynika z jednorodności czasu.
Całkowity moment pędu.
Ta ilość jest wektor i uzyskuje się go przez dodanie MCD wszystkich cząstek wchodzących w skład układu. Każda cząstka ma swoją własną MKD - spin i pęd orbitalny, wywołany ruchem cząstki względem ogólnego środka masy układu. Kwantyzacja MCD prowadzi do tego, że jego abs. ogrom J przyjmuje ściśle określone wartości: , gdzie J- liczba kwantowa, która może przyjmować nieujemne wartości całkowite i półcałkowite (liczba kwantowa orbitalnego MKD jest zawsze liczbą całkowitą). Projekcja MCD na kl. nazwa osi mag. liczba kwantowa i może przyjąć 2j+1 wartości: m jot = j, j-1,...,-J. Jeżeli k.-l. za chwilę J
yavl. suma dwóch innych momentów, to zgodnie z zasadami dodawania momentów w mechanice kwantowej liczba kwantowa J może przyjmować następujące wartości: J=|J 1 -J 2 |, |J 1 -J 2 -1|, ...., |J 1 +J 2 -1|, J 1 +J 2, za. Sumowanie większej liczby momentów odbywa się w podobny sposób. Dla zwięzłości zwyczajowo mówi się o systemach MCD J, sugerując moment, abs. którego wartość wynosi ; o mag. O liczbie kwantowej mówi się po prostu jako o projekcji pędu.
Podczas różnych transformacji układu położonego w polu centralnie symetrycznym, całkowite MCD jest zachowane, czyli podobnie jak energia odnosi się do wielkości zachowanych. Prawo zachowania MCD wynika z izotropii przestrzeni. W polu osiowo symetrycznym zachowany jest jedynie rzut całego MCD na oś symetrii.
Parytet stanu.
W mechanice kwantowej stany układu opisuje tzw. funkcje falowe. Parzystość charakteryzuje zmianę funkcji falowej układu podczas działania inwersji przestrzennej, tj. zmiana znaków współrzędnych wszystkich cząstek. Przy takim działaniu energia się nie zmienia, natomiast funkcja falowa może albo pozostać niezmieniona (stan parzysty), albo zmienić swój znak na przeciwny (stan nieparzysty). Parytet P przyjmuje odpowiednio dwie wartości. Jeśli system działa nuklearnie lub elektromagnetycznie. sił parytet zostaje zachowany w przemianach atomowych, molekularnych i jądrowych, tj. ilość ta odnosi się również do ilości konserwowanych. Prawo zachowania parytetu jest konsekwencją symetrii przestrzeni względem odbić lustrzanych i zostaje naruszona w procesach, w których zaangażowane są słabe oddziaływania.
Przejścia kwantowe
- przejścia układu z jednego stanu kwantowego do drugiego. Takie przejścia mogą prowadzić do obu zmian energii. stan systemu i jego cechy. zmiany. Są to przejścia związane, wolne, wolne (patrz Oddziaływanie promieniowania z materią), na przykład wzbudzenie, dezaktywacja, jonizacja, dysocjacja, rekombinacja. To także jest substancja chemiczna. i reakcje jądrowe. Przejścia mogą zachodzić pod wpływem promieniowania - przejścia radiacyjne (lub radiacyjne) lub gdy dany układ zderza się z cząstką. inny układ lub cząstka - przejścia niepromieniste. Ważna cecha zjawisk przejść kwantowych. jego prawdopodobieństwo w jednostkach. czasu, pokazując, jak często to przejście będzie występować. Wartość tę mierzy się w s -1. Prawdopodobieństwa promieniowania przejścia pomiędzy poziomami M I N (m>n) wraz z emisją lub absorpcją fotonu, którego energia jest równa , wyznacza się współczynnik. Einsteina A mn, B mn I Bnm. Przejście poziomu M na poziom N może wystąpić samoistnie. Prawdopodobieństwo emisji fotonów B mn w tym przypadku jest równe min. Przejścia typu pod wpływem promieniowania (przejścia indukowane) charakteryzują się prawdopodobieństwem emisji fotonu i absorpcji fotonu, gdzie jest gęstość energii promieniowania wraz z częstotliwością.
Możliwość przeprowadzenia przejścia kwantowego z zadanego e.e. na k.-l. kolejne U.E. oznacza, że cecha por. oczywiście czas, w którym system może znajdować się w tym UE. Definiuje się je jako odwrotność całkowitego prawdopodobieństwa zaniku danego poziomu, tj. suma prawdopodobieństw wszystkich możliwych przejść z rozważanego poziomu do wszystkich pozostałych. Na promieniowanie przejścia, całkowite prawdopodobieństwo wynosi , i . Skończoność czasu, zgodnie z zależnością niepewności, oznacza, że nie można określić poziomu energii w sposób absolutnie dokładny, tj. U.e. ma określoną szerokość. Dlatego emisja lub absorpcja fotonów podczas przejścia kwantowego nie następuje przy ściśle określonej częstotliwości, ale w pewnym przedziale częstotliwości leżącym w pobliżu tej wartości. Rozkład intensywności w tym przedziale określony jest profilem linii widmowej, który określa prawdopodobieństwo, że częstotliwość fotonu emitowanego lub absorbowanego podczas danego przejścia jest równa:
(1)
gdzie jest połowa szerokości profilu linii. Jeśli poszerzenie U.e. a linie widmowe powstają jedynie w wyniku spontanicznych przejść, wtedy takie poszerzenie nazywa się. naturalny. Jeżeli zderzenia układu z innymi cząstkami odgrywają pewną rolę w poszerzeniu, to poszerzenie ma charakter kombinowany i wartość należy zastąpić sumą, gdzie jest obliczana w podobny sposób, ale promieniowaniem. prawdopodobieństwa przejścia należy zastąpić prawdopodobieństwami kolizji.
Przejścia w układach kwantowych podlegają pewnym regułom selekcji, tj. zasady określające, jak liczby kwantowe charakteryzujące stan układu (MCD, parzystość itp.) mogą się zmieniać podczas przejścia. Zasady selekcji są najprościej sformułowane dla promieniowania. przejścia. W tym przypadku wyznaczają je właściwości stanu początkowego i końcowego, a także charakterystyka kwantowa emitowanego lub pochłoniętego fotonu, w szczególności jego MCD i parzystość. Najprawdopodobniej są to tzw elektryczne przejścia dipolowe. Przejścia te realizowane są pomiędzy poziomami o przeciwnych parzystościach, których pełne MCD różnią się o kwotę (przejście jest niemożliwe). W ramach ustalonej terminologii przejścia te nazywane są. dozwolony. Wszystkie inne rodzaje przejść (dipol magnetyczny, kwadrupol elektryczny itp.) Nazywa się. zabroniony. Znaczenie tego terminu polega jedynie na tym, że ich prawdopodobieństwa okazują się znacznie mniejsze niż prawdopodobieństwa dipolowych przejść elektrycznych. Jednak tak nie jest absolutnie zabronione.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Cały zespół zjawisk zwykle rozumiany pod terminem „właściwości elektroniczne niskowymiarowych układów elektronicznych” opiera się na podstawowym fakcie fizycznym: zmianie widma energetycznego elektronów i dziury w konstrukcjach o bardzo małych rozmiarach. Zademonstrujmy podstawową ideę kwantyzacji wielkości na przykładzie elektronów znajdujących się w bardzo cienkiej warstwie metalu lub półprzewodnika o grubości a.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Elektrony w folii znajdują się w studni potencjału o głębokości równej funkcji wyjścia. Głębokość studni potencjału można uznać za nieskończenie dużą, ponieważ funkcja pracy przekracza energię cieplną nośników o kilka rzędów wielkości. Typowe wartości funkcji pracy w większości ciał stałych to W = 4 -5 Oe. B, o kilka rzędów wielkości wyższy niż charakterystyczna energia cieplna nośników, mający rząd wielkości k. T równy w temperaturze pokojowej do 0,026 e. B. Zgodnie z prawami mechaniki kwantowej energia elektronów w takiej studni jest skwantowana, to znaczy może przyjmować tylko niektóre wartości dyskretne En, gdzie n może przyjmować wartości całkowite 1, 2, 3,… . Te dyskretne wartości energii nazywane są poziomami kwantyzacji wielkości.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Elektrony w folii znajdują się w studni potencjału o głębokości równej funkcji wyjścia. Głębokość studni potencjału można uznać za nieskończenie dużą, ponieważ funkcja pracy przekracza energię cieplną nośników o kilka rzędów wielkości. Typowe wartości funkcji pracy w większości ciał stałych to W = 4 -5 Oe. B, o kilka rzędów wielkości wyższy niż charakterystyczna energia cieplna nośników, mający rząd wielkości k. T równy w temperaturze pokojowej do 0,026 e. B. Zgodnie z prawami mechaniki kwantowej energia elektronów w takiej studni jest skwantowana, to znaczy może przyjmować tylko niektóre wartości dyskretne En, gdzie n może przyjmować wartości całkowite 1, 2, 3,… . Te dyskretne wartości energii nazywane są poziomami kwantyzacji wielkości.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Dla swobodnej cząstki o masie efektywnej m*, której ruch w krysztale w kierunku osi z jest ograniczony barierami nieprzeniknionymi (tj. barierami o nieskończonym potencjale energii), energia stanu podstawowego wzrasta w porównaniu ze stanem bez ograniczeń o ilość. Ten wzrost energii nazywany jest energią kwantyzacji wielkości cząstki. Energia kwantyzacji jest konsekwencją zasady nieoznaczoności w mechanice kwantowej. Jeśli cząstka jest ograniczona przestrzennie wzdłuż osi z w odległości a, niepewność składowej z jej pędu wzrasta o wielkość rzędu ħ/a. W związku z tym energia kinetyczna cząstki wzrasta o wielkość E 1. Dlatego rozpatrywany efekt często nazywany jest efektem wielkości kwantowej.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Dla swobodnej cząstki o masie efektywnej m*, której ruch w krysztale w kierunku osi z jest ograniczony barierami nieprzeniknionymi (tj. barierami o nieskończonym potencjale energii), energia stanu podstawowego wzrasta w porównaniu ze stanem bez ograniczeń o ilość. Ten wzrost energii nazywany jest energią kwantyzacji wielkości cząstki. Energia kwantyzacji jest konsekwencją zasady nieoznaczoności w mechanice kwantowej. Jeśli cząstka jest ograniczona przestrzennie wzdłuż osi z w odległości a, niepewność składowej z jej pędu wzrasta o wielkość rzędu ħ/a. W związku z tym energia kinetyczna cząstki wzrasta o wielkość E 1. Dlatego rozpatrywany efekt często nazywany jest efektem wielkości kwantowej.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Wniosek o kwantyzacji energii ruchu elektronicznego dotyczy tylko ruchu po studni potencjału (wzdłuż osi z). Potencjał studni nie wpływa na ruch w płaszczyźnie xy (równolegle do granic folii). W tej płaszczyźnie nośniki poruszają się jak swobodne nośniki i charakteryzują się, podobnie jak w masywnej próbce, ciągłym widmem energii kwadratowym w pędzie i masie efektywnej. Całkowita energia nośników w warstwie wielkości kwantowej ma mieszane, dyskretne widmo ciągłe
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Wniosek o kwantyzacji energii ruchu elektronicznego dotyczy tylko ruchu po studni potencjału (wzdłuż osi z). Potencjał studni nie wpływa na ruch w płaszczyźnie xy (równolegle do granic folii). W tej płaszczyźnie nośniki poruszają się jak swobodne nośniki i charakteryzują się, podobnie jak w masywnej próbce, ciągłym widmem energii kwadratowym w pędzie i masie efektywnej. Całkowita energia nośników w warstwie wielkości kwantowej ma mieszane, dyskretne widmo ciągłe
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wielkości Oprócz zwiększenia minimalnej energii cząstki, efekt wielkości kwantowej prowadzi również do kwantyzacji energii jej stanów wzbudzonych. Widmo energetyczne błony kwantowej - pęd nośników ładunku w płaszczyźnie błony
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wielkości Oprócz zwiększenia minimalnej energii cząstki, efekt wielkości kwantowej prowadzi również do kwantyzacji energii jej stanów wzbudzonych. Widmo energetyczne błony kwantowej - pęd nośników ładunku w płaszczyźnie błony
 WŁAŚCIWOŚCI ELEKTRONICZNE MISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wielkości Niech elektrony w układzie mają energie mniejsze niż E 2, a zatem należą do niższego poziomu kwantyzacji wielkości. Wtedy żaden proces elastyczny (np. rozpraszanie na domieszkach czy fononach akustycznych), a także wzajemne rozpraszanie elektronów nie jest w stanie zmienić liczby kwantowej n, przenosząc elektron na wyższy poziom, gdyż wymagałoby to dodatkowej energii. Oznacza to, że elektrony podczas rozpraszania elastycznego mogą zmieniać swój pęd jedynie w płaszczyźnie błony, czyli zachowują się jak cząstki czysto dwuwymiarowe. Dlatego struktury wielkości kwantowej, w których wypełniony jest tylko jeden poziom kwantowy, nazywane są często dwuwymiarowymi strukturami elektronicznymi.
WŁAŚCIWOŚCI ELEKTRONICZNE MISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wielkości Niech elektrony w układzie mają energie mniejsze niż E 2, a zatem należą do niższego poziomu kwantyzacji wielkości. Wtedy żaden proces elastyczny (np. rozpraszanie na domieszkach czy fononach akustycznych), a także wzajemne rozpraszanie elektronów nie jest w stanie zmienić liczby kwantowej n, przenosząc elektron na wyższy poziom, gdyż wymagałoby to dodatkowej energii. Oznacza to, że elektrony podczas rozpraszania elastycznego mogą zmieniać swój pęd jedynie w płaszczyźnie błony, czyli zachowują się jak cząstki czysto dwuwymiarowe. Dlatego struktury wielkości kwantowej, w których wypełniony jest tylko jeden poziom kwantowy, nazywane są często dwuwymiarowymi strukturami elektronicznymi.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Istnieją inne możliwe struktury kwantowe, w których ruch nośników jest ograniczony nie w jednym, ale w dwóch kierunkach, jak w mikroskopijnym drucie lub nici (niciach lub drutach kwantowych). W tym przypadku nośniki mogą swobodnie poruszać się tylko w jednym kierunku, wzdłuż gwintu (nazwijmy to osią x). W przekroju (płaszczyzna yz) energia jest skwantowana i przyjmuje dyskretne wartości Emn (jak każdy ruch dwuwymiarowy, opisywany jest przez dwie liczby kwantowe m i n). Pełne widmo jest również dyskretnie ciągłe, ale ma tylko jeden ciągły stopień swobody:
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Istnieją inne możliwe struktury kwantowe, w których ruch nośników jest ograniczony nie w jednym, ale w dwóch kierunkach, jak w mikroskopijnym drucie lub nici (niciach lub drutach kwantowych). W tym przypadku nośniki mogą swobodnie poruszać się tylko w jednym kierunku, wzdłuż gwintu (nazwijmy to osią x). W przekroju (płaszczyzna yz) energia jest skwantowana i przyjmuje dyskretne wartości Emn (jak każdy ruch dwuwymiarowy, opisywany jest przez dwie liczby kwantowe m i n). Pełne widmo jest również dyskretnie ciągłe, ale ma tylko jeden ciągły stopień swobody:
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Możliwe jest także tworzenie struktur kwantowych przypominających sztuczne atomy, w których ruch nośników jest ograniczony we wszystkich trzech kierunkach (kropki kwantowe). W kropkach kwantowych widmo energii nie zawiera już składowej ciągłej, to znaczy nie składa się z podpasm, ale jest czysto dyskretne. Podobnie jak w atomie, jest to opisane trzema dyskretnymi liczbami kwantowymi (nie licząc spinu) i można je zapisać jako E = Elmn i podobnie jak w atomie poziomy energii mogą być zdegenerowane i zależeć tylko od jednej lub dwóch liczb. Wspólną cechą struktur niskowymiarowych jest fakt, że jeśli przynajmniej w jednym kierunku ruch nośników zostanie ograniczony do bardzo małego obszaru porównywalnego wielkością do długości fali de Broglie’a nośników, to ich widmo energii zmienia się zauważalnie i staje się częściowo lub całkowicie dyskretny.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Zasada kwantyzacji wymiarowej Możliwe jest także tworzenie struktur kwantowych przypominających sztuczne atomy, w których ruch nośników jest ograniczony we wszystkich trzech kierunkach (kropki kwantowe). W kropkach kwantowych widmo energii nie zawiera już składowej ciągłej, to znaczy nie składa się z podpasm, ale jest czysto dyskretne. Podobnie jak w atomie, jest to opisane trzema dyskretnymi liczbami kwantowymi (nie licząc spinu) i można je zapisać jako E = Elmn i podobnie jak w atomie poziomy energii mogą być zdegenerowane i zależeć tylko od jednej lub dwóch liczb. Wspólną cechą struktur niskowymiarowych jest fakt, że jeśli przynajmniej w jednym kierunku ruch nośników zostanie ograniczony do bardzo małego obszaru porównywalnego wielkością do długości fali de Broglie’a nośników, to ich widmo energii zmienia się zauważalnie i staje się częściowo lub całkowicie dyskretny.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Definicje Kropki kwantowe to struktury, których wymiary we wszystkich trzech kierunkach odpowiadają kilku odległościom międzyatomowym (struktury zerowymiarowe). Druty kwantowe (nici) - druty kwantowe - struktury, których wymiary w dwóch kierunkach są równe kilku odległościom międzyatomowym, a w trzecim - wartość makroskopowa (struktury jednowymiarowe). Studnie kwantowe to struktury, których rozmiar w jednym kierunku wynosi kilka odległości międzyatomowych (struktury dwuwymiarowe).
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Definicje Kropki kwantowe to struktury, których wymiary we wszystkich trzech kierunkach odpowiadają kilku odległościom międzyatomowym (struktury zerowymiarowe). Druty kwantowe (nici) - druty kwantowe - struktury, których wymiary w dwóch kierunkach są równe kilku odległościom międzyatomowym, a w trzecim - wartość makroskopowa (struktury jednowymiarowe). Studnie kwantowe to struktury, których rozmiar w jednym kierunku wynosi kilka odległości międzyatomowych (struktury dwuwymiarowe).
 WŁAŚCIWOŚCI ELEKTRONICZNE MISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozmiary minimalne i maksymalne Dolną granicę kwantyzacji rozmiarów wyznacza rozmiar krytyczny Dmin, przy którym w strukturze kwantowo-wymiarowej istnieje co najmniej jeden poziom elektronowy. Dmin zależy od przerwy wzbronionej przewodnictwa DEc w odpowiednim heterozłączu używanym do otrzymania struktur studni kwantowych. W studni kwantowej co najmniej jeden poziom elektronowy istnieje, jeśli DEc przekracza wartość h – stała Plancka, me* to efektywna masa elektronu, DE 1 QW to pierwszy poziom w prostokątnej studni kwantowej o nieskończonych ściankach.
WŁAŚCIWOŚCI ELEKTRONICZNE MISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozmiary minimalne i maksymalne Dolną granicę kwantyzacji rozmiarów wyznacza rozmiar krytyczny Dmin, przy którym w strukturze kwantowo-wymiarowej istnieje co najmniej jeden poziom elektronowy. Dmin zależy od przerwy wzbronionej przewodnictwa DEc w odpowiednim heterozłączu używanym do otrzymania struktur studni kwantowych. W studni kwantowej co najmniej jeden poziom elektronowy istnieje, jeśli DEc przekracza wartość h – stała Plancka, me* to efektywna masa elektronu, DE 1 QW to pierwszy poziom w prostokątnej studni kwantowej o nieskończonych ściankach.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Wymiary minimalne i maksymalne Jeżeli odległość pomiędzy poziomami energii staje się porównywalna z energią cieplną k. BT, wówczas populacja wysokich poziomów wzrasta. Dla kropki kwantowej warunek, w którym można zaniedbać populację wyższych poziomów leżących, zapisuje się jako E 1 QD, E 2 QD - odpowiednio energie pierwszego i drugiego poziomu kwantyzacji wielkości. Oznacza to, że korzyści wynikające z kwantyzacji rozmiaru można w pełni wykorzystać, jeśli warunek ten wyznacza górne granice kwantyzacji rozmiaru. Dla Ga. As-Alx. Ga1-x. Ponieważ ta wartość wynosi 12 nm.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Wymiary minimalne i maksymalne Jeżeli odległość pomiędzy poziomami energii staje się porównywalna z energią cieplną k. BT, wówczas populacja wysokich poziomów wzrasta. Dla kropki kwantowej warunek, w którym można zaniedbać populację wyższych poziomów leżących, zapisuje się jako E 1 QD, E 2 QD - odpowiednio energie pierwszego i drugiego poziomu kwantyzacji wielkości. Oznacza to, że korzyści wynikające z kwantyzacji rozmiaru można w pełni wykorzystać, jeśli warunek ten wyznacza górne granice kwantyzacji rozmiaru. Dla Ga. As-Alx. Ga1-x. Ponieważ ta wartość wynosi 12 nm.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Ważną cechą każdego układu elektronicznego, wraz z jego widmem energetycznym, jest gęstość stanów g(E) (liczba stanów na jednostkę przedziału energii E ). Dla kryształów trójwymiarowych gęstość stanów wyznacza się za pomocą cyklicznych warunków brzegowych Borna-Karmana, z których wynika, że składowe wektora fali elektronowej nie zmieniają się w sposób ciągły, lecz przyjmują szereg wartości dyskretnych, tutaj ni = 0 , ± 1, ± 2, ± 3, i są wymiarami kryształu (w kształcie sześcianu o boku L). Objętość przestrzeni k na stan kwantowy jest równa (2)3/V, gdzie V = L 3 jest objętością kryształu.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Ważną cechą każdego układu elektronicznego, wraz z jego widmem energetycznym, jest gęstość stanów g(E) (liczba stanów na jednostkę przedziału energii E ). Dla kryształów trójwymiarowych gęstość stanów wyznacza się za pomocą cyklicznych warunków brzegowych Borna-Karmana, z których wynika, że składowe wektora fali elektronowej nie zmieniają się w sposób ciągły, lecz przyjmują szereg wartości dyskretnych, tutaj ni = 0 , ± 1, ± 2, ± 3, i są wymiarami kryształu (w kształcie sześcianu o boku L). Objętość przestrzeni k na stan kwantowy jest równa (2)3/V, gdzie V = L 3 jest objętością kryształu.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Zatem liczba stanów elektronowych na element objętościowy dk = dkxdkydkz, obliczona na jednostkę objętości, będzie równa tutaj, współczynnik 2 uwzględnia dwa możliwe orientacje wirowania. Liczba stanów na jednostkę objętości w przestrzeni odwrotnej, czyli gęstość stanów) nie zależy od wektora falowego.Innymi słowy, w przestrzeni odwrotnej dozwolone stany są rozmieszczone ze stałą gęstością.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Zatem liczba stanów elektronowych na element objętościowy dk = dkxdkydkz, obliczona na jednostkę objętości, będzie równa tutaj, współczynnik 2 uwzględnia dwa możliwe orientacje wirowania. Liczba stanów na jednostkę objętości w przestrzeni odwrotnej, czyli gęstość stanów) nie zależy od wektora falowego.Innymi słowy, w przestrzeni odwrotnej dozwolone stany są rozmieszczone ze stałą gęstością.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych W ogólnym przypadku obliczenie funkcji gęstości stanów ze względu na energię jest praktycznie niemożliwe, ponieważ powierzchnie izoenergetyczne mogą mieć dość złożony kształt. W najprostszym przypadku izotropowego prawa dyspersji parabolicznej, obowiązującego dla krawędzi pasm energii, można znaleźć liczbę stanów kwantowych w objętości warstwy sferycznej zamkniętej pomiędzy dwiema bliskimi powierzchniami izoenergetycznymi odpowiadającymi energiom E i E+d. MI.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych W ogólnym przypadku obliczenie funkcji gęstości stanów ze względu na energię jest praktycznie niemożliwe, ponieważ powierzchnie izoenergetyczne mogą mieć dość złożony kształt. W najprostszym przypadku izotropowego prawa dyspersji parabolicznej, obowiązującego dla krawędzi pasm energii, można znaleźć liczbę stanów kwantowych w objętości warstwy sferycznej zamkniętej pomiędzy dwiema bliskimi powierzchniami izoenergetycznymi odpowiadającymi energiom E i E+d. MI.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Objętość warstwy sferycznej w przestrzeni k. dk – grubość warstwy. Objętość ta będzie stanowić d. N stanów Biorąc pod uwagę związek E i k zgodnie z prawem parabolicznym otrzymujemy Stąd gęstość stanów w energii będzie równa m* - efektywna masa elektronu
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Objętość warstwy sferycznej w przestrzeni k. dk – grubość warstwy. Objętość ta będzie stanowić d. N stanów Biorąc pod uwagę związek E i k zgodnie z prawem parabolicznym otrzymujemy Stąd gęstość stanów w energii będzie równa m* - efektywna masa elektronu
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach o zredukowanej wymiarowości Zatem w trójwymiarowych kryształach o parabolicznym widmie energii wraz ze wzrostem energii gęstość dopuszczalnych poziomów energii (gęstość stanów) będzie wzrastać proporcjonalnie do gęstość poziomów w paśmie przewodnictwa i w paśmie walencyjnym. Powierzchnia zacienionych obszarów jest proporcjonalna do liczby poziomów w przedziale energetycznym d. mi
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach o zredukowanej wymiarowości Zatem w trójwymiarowych kryształach o parabolicznym widmie energii wraz ze wzrostem energii gęstość dopuszczalnych poziomów energii (gęstość stanów) będzie wzrastać proporcjonalnie do gęstość poziomów w paśmie przewodnictwa i w paśmie walencyjnym. Powierzchnia zacienionych obszarów jest proporcjonalna do liczby poziomów w przedziale energetycznym d. mi
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Obliczmy gęstość stanów dla układu dwuwymiarowego. Całkowita energia nośna dla prawa izotropowej dyspersji parabolicznej w warstwie kwantowej, jak pokazano powyżej, ma mieszane dyskretnie ciągłe widmo.W układzie dwuwymiarowym stany elektronu przewodnictwa są określone przez trzy liczby (n, kx , kk). Widmo energii podzielone jest na osobne dwuwymiarowe podstrefy En odpowiadające ustalonym wartościom n.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Obliczmy gęstość stanów dla układu dwuwymiarowego. Całkowita energia nośna dla prawa izotropowej dyspersji parabolicznej w warstwie kwantowej, jak pokazano powyżej, ma mieszane dyskretnie ciągłe widmo.W układzie dwuwymiarowym stany elektronu przewodnictwa są określone przez trzy liczby (n, kx , kk). Widmo energii podzielone jest na osobne dwuwymiarowe podstrefy En odpowiadające ustalonym wartościom n.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Krzywe stałej energii są okręgami w przestrzeni odwrotnej. Każda dyskretna liczba kwantowa n odpowiada wartości bezwzględnej składowej z wektora falowego. Dlatego objętość w przestrzeni odwrotnej ograniczona zamkniętą powierzchnią o danej energii E w przypadku układu dwuwymiarowego jest dzielona na liczba sekcji.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Krzywe stałej energii są okręgami w przestrzeni odwrotnej. Każda dyskretna liczba kwantowa n odpowiada wartości bezwzględnej składowej z wektora falowego. Dlatego objętość w przestrzeni odwrotnej ograniczona zamkniętą powierzchnią o danej energii E w przypadku układu dwuwymiarowego jest dzielona na liczba sekcji.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Wyznaczmy zależność gęstości stanów od energii dla układu dwuwymiarowego. Aby to zrobić, dla danego n znajdujemy obszar S pierścienia ograniczony dwiema powierzchniami izoenergetycznymi odpowiadającymi energiom E i E+d. E: Oto wielkość dwuwymiarowego wektora falowego odpowiadająca danym n i E; dkr – szerokość pierścienia. Ponieważ jeden stan w płaszczyźnie (kxky) odpowiada obszarowi, w którym L 2 jest obszarem dwuwymiarowej folii o grubości a, liczba stanów elektronowych w pierścieniu, obliczona na jednostkę objętości kryształu, będzie wynosić równy, biorąc pod uwagę spin elektronu
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Wyznaczmy zależność gęstości stanów od energii dla układu dwuwymiarowego. Aby to zrobić, dla danego n znajdujemy obszar S pierścienia ograniczony dwiema powierzchniami izoenergetycznymi odpowiadającymi energiom E i E+d. E: Oto wielkość dwuwymiarowego wektora falowego odpowiadająca danym n i E; dkr – szerokość pierścienia. Ponieważ jeden stan w płaszczyźnie (kxky) odpowiada obszarowi, w którym L 2 jest obszarem dwuwymiarowej folii o grubości a, liczba stanów elektronowych w pierścieniu, obliczona na jednostkę objętości kryształu, będzie wynosić równy, biorąc pod uwagę spin elektronu
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Ponieważ tutaj jest energia odpowiadająca dołowi n-tego podpasma. Zatem gęstość stanów w dwuwymiarowym filmie, gdzie Q(Y) jest funkcją jednostkową Heaviside'a, Q(Y) =1 dla Y≥ 0 i Q(Y) =0 dla Y
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Ponieważ tutaj jest energia odpowiadająca dołowi n-tego podpasma. Zatem gęstość stanów w dwuwymiarowym filmie, gdzie Q(Y) jest funkcją jednostkową Heaviside'a, Q(Y) =1 dla Y≥ 0 i Q(Y) =0 dla Y
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w warstwie dwuwymiarowej można również przedstawić jako część całkowitą równą liczbie podpasm, których dół znajduje się poniżej energii E. Zatem , dla filmów dwuwymiarowych z prawem dyspersji parabolicznej gęstość stanów w dowolnej podstrefie jest stała i nie zależy od energii. Każde podpasmo ma równy udział w ogólnej gęstości stanów. Przy stałej grubości warstwy gęstość stanów zmienia się gwałtownie, gdy nie zmienia się o jedność.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w warstwie dwuwymiarowej można również przedstawić jako część całkowitą równą liczbie podpasm, których dół znajduje się poniżej energii E. Zatem , dla filmów dwuwymiarowych z prawem dyspersji parabolicznej gęstość stanów w dowolnej podstrefie jest stała i nie zależy od energii. Każde podpasmo ma równy udział w ogólnej gęstości stanów. Przy stałej grubości warstwy gęstość stanów zmienia się gwałtownie, gdy nie zmienia się o jedność.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Zależność gęstości stanów dwuwymiarowej warstwy od energii (a) i grubości a (b).
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Zależność gęstości stanów dwuwymiarowej warstwy od energii (a) i grubości a (b).
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych W przypadku dowolnego prawa dyspersji lub innego rodzaju studni potencjału zależność gęstości stanu od energii i grubości warstwy może różnić się od podanych powyżej, ale główna cecha – niemonotoniczne zachowanie – pozostanie.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych W przypadku dowolnego prawa dyspersji lub innego rodzaju studni potencjału zależność gęstości stanu od energii i grubości warstwy może różnić się od podanych powyżej, ale główna cecha – niemonotoniczne zachowanie – pozostanie.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Obliczmy gęstość stanów dla struktury jednowymiarowej - nici kwantowej. Izotropowe prawo dyspersji parabolicznej w tym przypadku można zapisać w postaci x jest skierowane wzdłuż nici kwantowej, d jest grubością nici kwantowej wzdłuż osi y i z, kx jest jednowymiarowym wektorem falowym. m, n są dodatnimi liczbami całkowitymi charakteryzującymi oś gdzie podpasm kwantowych. Widmo energii nici kwantowej jest zatem podzielone na osobne, nakładające się jednowymiarowe podpasma (parabole). Ruch elektronów wzdłuż osi x okazuje się swobodny (ale z masą efektywną), natomiast ruch wzdłuż pozostałych dwóch osi jest ograniczony.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Obliczmy gęstość stanów dla struktury jednowymiarowej - nici kwantowej. Izotropowe prawo dyspersji parabolicznej w tym przypadku można zapisać w postaci x jest skierowane wzdłuż nici kwantowej, d jest grubością nici kwantowej wzdłuż osi y i z, kx jest jednowymiarowym wektorem falowym. m, n są dodatnimi liczbami całkowitymi charakteryzującymi oś gdzie podpasm kwantowych. Widmo energii nici kwantowej jest zatem podzielone na osobne, nakładające się jednowymiarowe podpasma (parabole). Ruch elektronów wzdłuż osi x okazuje się swobodny (ale z masą efektywną), natomiast ruch wzdłuż pozostałych dwóch osi jest ograniczony.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Widmo energii elektronów dla nici kwantowej
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Widmo energii elektronów dla nici kwantowej
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w zależności od energii Liczba stanów kwantowych na przedział dkx, liczona na jednostkę objętości gdzie jest energią odpowiadającą dołowi podpasma z dane n i m.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w zależności od energii Liczba stanów kwantowych na przedział dkx, liczona na jednostkę objętości gdzie jest energią odpowiadającą dołowi podpasma z dane n i m.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w funkcji energii Zatem Zatem Dlatego Przy wyprowadzaniu tego wzoru należy uwzględnić degenerację spinową stanów oraz fakt, że jeden przedział d wynosi uwzględnić. E odpowiada dwóm przedziałom ±dkx każdego podpasma, dla których (E-En, m) > 0. Energia E jest mierzona od dołu pasma przewodnictwa masywnej próbki.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w funkcji energii Zatem Zatem Dlatego Przy wyprowadzaniu tego wzoru należy uwzględnić degenerację spinową stanów oraz fakt, że jeden przedział d wynosi uwzględnić. E odpowiada dwóm przedziałom ±dkx każdego podpasma, dla których (E-En, m) > 0. Energia E jest mierzona od dołu pasma przewodnictwa masywnej próbki.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w nici kwantowej na energię Zależność gęstości stanów nici kwantowej na energię. Liczby obok krzywych pokazują liczby kwantowe n i m. Czynniki degeneracji poziomów podpasm podano w nawiasach.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w nici kwantowej na energię Zależność gęstości stanów nici kwantowej na energię. Liczby obok krzywych pokazują liczby kwantowe n i m. Czynniki degeneracji poziomów podpasm podano w nawiasach.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w funkcji energii W obrębie danego podpasma gęstość stanów maleje wraz ze wzrostem energii. Całkowita gęstość stanów jest superpozycją identycznych funkcji malejących (odpowiadających poszczególnym podpasmom) przesuniętych wzdłuż osi energii. Przy E = E m, n gęstość stanów jest równa nieskończoności. Podpasma o liczbach kwantowych n m okazują się podwójnie zdegenerowane (tylko dla Ly = Lz d).
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w wątku kwantowym w funkcji energii W obrębie danego podpasma gęstość stanów maleje wraz ze wzrostem energii. Całkowita gęstość stanów jest superpozycją identycznych funkcji malejących (odpowiadających poszczególnym podpasmom) przesuniętych wzdłuż osi energii. Przy E = E m, n gęstość stanów jest równa nieskończoności. Podpasma o liczbach kwantowych n m okazują się podwójnie zdegenerowane (tylko dla Ly = Lz d).
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Przy trójwymiarowym ograniczeniu ruchu cząstek dochodzimy do problemu znalezienia dozwolonych stanów w kwantze system kropkowy lub zerowymiarowy. Korzystając z przybliżenia masy efektywnej i prawa dyspersji parabolicznej, dla krawędzi izotropowego pasma energii widmo dozwolonych stanów kropki kwantowej o tych samych wymiarach d wzdłuż wszystkich trzech osi współrzędnych będzie miało postać n, m, l = 1 , 2, 3 ... - liczby dodatnie numerujące podpasma. Widmo energii kropki kwantowej to zbiór dyskretnych dozwolonych stanów odpowiadających ustalonym n, m, l.
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Przy trójwymiarowym ograniczeniu ruchu cząstek dochodzimy do problemu znalezienia dozwolonych stanów w kwantze system kropkowy lub zerowymiarowy. Korzystając z przybliżenia masy efektywnej i prawa dyspersji parabolicznej, dla krawędzi izotropowego pasma energii widmo dozwolonych stanów kropki kwantowej o tych samych wymiarach d wzdłuż wszystkich trzech osi współrzędnych będzie miało postać n, m, l = 1 , 2, 3 ... - liczby dodatnie numerujące podpasma. Widmo energii kropki kwantowej to zbiór dyskretnych dozwolonych stanów odpowiadających ustalonym n, m, l.
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Liczba stanów w podzakresach odpowiadających jednemu zbiorowi n, m, l, w przeliczeniu na jednostkę objętości, Suma liczba stanów o tej samej energii, liczona na jednostkę objętości. O degeneracji poziomów decyduje przede wszystkim symetria problemu. g – współczynnik degeneracji poziomu
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Liczba stanów w podzakresach odpowiadających jednemu zbiorowi n, m, l, w przeliczeniu na jednostkę objętości, Suma liczba stanów o tej samej energii, liczona na jednostkę objętości. O degeneracji poziomów decyduje przede wszystkim symetria problemu. g – współczynnik degeneracji poziomu
 WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii O degeneracji poziomów decyduje przede wszystkim symetria problemu. Przykładowo dla rozważanego przypadku kropki kwantowej o tych samych wymiarach we wszystkich trzech wymiarach poziomy będą zdegenerowane trzykrotnie, jeśli dwie liczby kwantowe będą sobie równe i nie będą równe trzeciej, oraz zdegenerowane sześciokrotnie, jeśli wszystkie liczby kwantowe liczby nie są sobie równe. Specyficzny rodzaj potencjału może także prowadzić do dodatkowej, tzw. losowej degeneracji. Np. dla rozważanej kropki kwantowej do potrójnej degeneracji poziomów E(5, 1, 1); E(1, 5, 1); Do E(1, 1, 5), powiązanego z symetrią problemu, dodaje się losową degenerację E(3, 3, 3) (n 2+m 2+l 2=27 zarówno w pierwszym, jak i drugim przypadku), związaną z potencjałem ograniczającym formę (nieskończona prostokątna studnia potencjału).
WŁAŚCIWOŚCI ELEKTRONICZNE NISKOWYMIAROWYCH UKŁADÓW ELEKTRONICZNYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii O degeneracji poziomów decyduje przede wszystkim symetria problemu. Przykładowo dla rozważanego przypadku kropki kwantowej o tych samych wymiarach we wszystkich trzech wymiarach poziomy będą zdegenerowane trzykrotnie, jeśli dwie liczby kwantowe będą sobie równe i nie będą równe trzeciej, oraz zdegenerowane sześciokrotnie, jeśli wszystkie liczby kwantowe liczby nie są sobie równe. Specyficzny rodzaj potencjału może także prowadzić do dodatkowej, tzw. losowej degeneracji. Np. dla rozważanej kropki kwantowej do potrójnej degeneracji poziomów E(5, 1, 1); E(1, 5, 1); Do E(1, 1, 5), powiązanego z symetrią problemu, dodaje się losową degenerację E(3, 3, 3) (n 2+m 2+l 2=27 zarówno w pierwszym, jak i drugim przypadku), związaną z potencjałem ograniczającym formę (nieskończona prostokątna studnia potencjału).
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Rozkład liczby dozwolonych stanów N w paśmie przewodnictwa dla kropki kwantowej o tych samych wymiarach we wszystkich trzy wymiary. Liczby reprezentują liczby kwantowe; Czynniki degeneracji poziomu podano w nawiasach.
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Rozkład stanów kwantowych w strukturach niskowymiarowych Gęstość stanów w kropce kwantowej w funkcji energii Rozkład liczby dozwolonych stanów N w paśmie przewodnictwa dla kropki kwantowej o tych samych wymiarach we wszystkich trzy wymiary. Liczby reprezentują liczby kwantowe; Czynniki degeneracji poziomu podano w nawiasach.
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Właściwości elektronów w równowadze w półprzewodnikach zależą od funkcji rozkładu Fermiego, która określa prawdopodobieństwo, że elektron znajdzie się w stanie kwantowym o energii E EF - poziom Fermiego lub potencjał elektrochemiczny, T - temperatura bezwzględna, k - stała Boltzmanna. Obliczanie różnych wielkości statystycznych jest znacznie uproszczone, jeśli poziom Fermiego leży w przerwie energetycznej i jest znacznie oddalony od dna pasma przewodnictwa Ec (Ec – EF) > k. T. Wtedy w rozkładzie Fermiego-Diraca można pominąć jednostkę w mianowniku i przejść do rozkładu statystyki klasycznej Maxwella-Boltzmanna. Dzieje się tak w przypadku niezdegenerowanego półprzewodnika
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Właściwości elektronów w równowadze w półprzewodnikach zależą od funkcji rozkładu Fermiego, która określa prawdopodobieństwo, że elektron znajdzie się w stanie kwantowym o energii E EF - poziom Fermiego lub potencjał elektrochemiczny, T - temperatura bezwzględna, k - stała Boltzmanna. Obliczanie różnych wielkości statystycznych jest znacznie uproszczone, jeśli poziom Fermiego leży w przerwie energetycznej i jest znacznie oddalony od dna pasma przewodnictwa Ec (Ec – EF) > k. T. Wtedy w rozkładzie Fermiego-Diraca można pominąć jednostkę w mianowniku i przejść do rozkładu statystyki klasycznej Maxwella-Boltzmanna. Dzieje się tak w przypadku niezdegenerowanego półprzewodnika
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Funkcja rozkładu stanów w paśmie przewodnictwa g(E), funkcja Fermiego-Diraca dla trzech temperatur i funkcja Maxwella-Boltzmanna dla trójwymiarowych gaz elektronowy. W T = 0 funkcja Fermiego-Diraca ma postać funkcji nieciągłej. Dla E EF funkcja wynosi zero, a odpowiadające jej stany kwantowe są całkowicie dowolne. W T > 0 funkcja Fermiego. Rozmazy Diraca znajdują się w pobliżu energii Fermiego, gdzie szybko zmienia się ona z 1 na 0 i rozmaz ten jest proporcjonalny do k. T, tj. im wyższa temperatura, tym większa. (ryc. 1. 4. Gurtow)
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Funkcja rozkładu stanów w paśmie przewodnictwa g(E), funkcja Fermiego-Diraca dla trzech temperatur i funkcja Maxwella-Boltzmanna dla trójwymiarowych gaz elektronowy. W T = 0 funkcja Fermiego-Diraca ma postać funkcji nieciągłej. Dla E EF funkcja wynosi zero, a odpowiadające jej stany kwantowe są całkowicie dowolne. W T > 0 funkcja Fermiego. Rozmazy Diraca znajdują się w pobliżu energii Fermiego, gdzie szybko zmienia się ona z 1 na 0 i rozmaz ten jest proporcjonalny do k. T, tj. im wyższa temperatura, tym większa. (ryc. 1. 4. Gurtow)
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Stężenie elektronów w paśmie przewodnictwa wyznacza się sumując po wszystkich stanach.Zauważ, że jako górną granicę tej całki musielibyśmy przyjąć energia górnej krawędzi pasma przewodnictwa. Ponieważ jednak funkcja Fermiego-Diraca dla energii E >EF maleje wykładniczo szybko wraz ze wzrostem energii, zastąpienie górnej granicy nieskończonością nie zmienia wartości całki. Podstawiając wartości funkcji do całki, otrzymujemy -efektywną gęstość stanów w paśmie przewodnictwa
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Trójwymiarowe układy elektroniczne Stężenie elektronów w paśmie przewodnictwa wyznacza się sumując po wszystkich stanach.Zauważ, że jako górną granicę tej całki musielibyśmy przyjąć energia górnej krawędzi pasma przewodnictwa. Ponieważ jednak funkcja Fermiego-Diraca dla energii E >EF maleje wykładniczo szybko wraz ze wzrostem energii, zastąpienie górnej granicy nieskończonością nie zmienia wartości całki. Podstawiając wartości funkcji do całki, otrzymujemy -efektywną gęstość stanów w paśmie przewodnictwa
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Dwuwymiarowe układy elektroniczne Wyznaczmy stężenie nośników ładunku w dwuwymiarowym gazie elektronowym. Ponieważ gęstość stanów dwuwymiarowego gazu elektronowego Otrzymujemy Tutaj górną granicę integracji przyjmuje się również równą nieskończoności, biorąc pod uwagę ostrą zależność funkcji rozkładu Fermiego-Diraca od energii. Integracja gdzie
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Dwuwymiarowe układy elektroniczne Wyznaczmy stężenie nośników ładunku w dwuwymiarowym gazie elektronowym. Ponieważ gęstość stanów dwuwymiarowego gazu elektronowego Otrzymujemy Tutaj górną granicę integracji przyjmuje się również równą nieskończoności, biorąc pod uwagę ostrą zależność funkcji rozkładu Fermiego-Diraca od energii. Integracja gdzie
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Dwuwymiarowe układy elektroniczne Dla niezdegenerowanego gazu elektronowego, gdy W przypadku ultracienkich warstw można uwzględnić wypełnienie tylko dolnego podpasma Dla silna degeneracja gazu elektronowego, gdy n 0 jest częścią całkowitą
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW MISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Dwuwymiarowe układy elektroniczne Dla niezdegenerowanego gazu elektronowego, gdy W przypadku ultracienkich warstw można uwzględnić wypełnienie tylko dolnego podpasma Dla silna degeneracja gazu elektronowego, gdy n 0 jest częścią całkowitą
 WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Należy zauważyć, że w układach kwantowych, ze względu na mniejszą gęstość stanów, stan całkowitej degeneracji nie wymaga ekstremalnie wysokich stężeń ani niskich temperatur i jest dość często realizowane w eksperymentach. Na przykład w n-Ga. Ponieważ przy N 2 D = 1012 cm-2 degeneracja nastąpi już w temperaturze pokojowej. W wątkach kwantowych całka do obliczeń, w przeciwieństwie do przypadków dwuwymiarowych i trójwymiarowych, nie jest obliczana analitycznie przy dowolnej degeneracji, a proste wzory można zapisać tylko w ograniczonych przypadkach. W niezdegenerowanym jednowymiarowym gazie elektronowym w przypadku ultracienkich włókien, gdy można uwzględnić wypełnienie energią jedynie najniższego poziomu E 11 stężenie elektronów gdzie jest jednowymiarową efektywną gęstością stanów
WŁAŚCIWOŚCI ELEKTRONICZNE UKŁADÓW NISKOWYMIAROWYCH Statystyka nośników w strukturach niskowymiarowych Należy zauważyć, że w układach kwantowych, ze względu na mniejszą gęstość stanów, stan całkowitej degeneracji nie wymaga ekstremalnie wysokich stężeń ani niskich temperatur i jest dość często realizowane w eksperymentach. Na przykład w n-Ga. Ponieważ przy N 2 D = 1012 cm-2 degeneracja nastąpi już w temperaturze pokojowej. W wątkach kwantowych całka do obliczeń, w przeciwieństwie do przypadków dwuwymiarowych i trójwymiarowych, nie jest obliczana analitycznie przy dowolnej degeneracji, a proste wzory można zapisać tylko w ograniczonych przypadkach. W niezdegenerowanym jednowymiarowym gazie elektronowym w przypadku ultracienkich włókien, gdy można uwzględnić wypełnienie energią jedynie najniższego poziomu E 11 stężenie elektronów gdzie jest jednowymiarową efektywną gęstością stanów
Układy kwantowe identycznych cząstek
Kwantowe cechy zachowania mikrocząstek, odróżniające je od właściwości obiektów makroskopowych, pojawiają się nie tylko przy rozważaniu ruchu jednej cząstki, ale także przy analizie zachowania systemy mikrocząstki . Najwyraźniej widać to na przykładzie układów fizycznych składających się z identycznych cząstek - układów elektronów, protonów, neutronów itp.
Dla systemu z N cząstki posiadające masy T 01 , T 02 , … T 0 I , … M 0 N, posiadający współrzędne ( X I , y I , z I) funkcję falową można przedstawić jako
Ψ (X 1 , y 1 , z 1 , … X I , y I , z I , … X N , y N , z N , T) .
Dla podstawowej objętości
dV I = dx I . dy I . dz I
ogrom
w =
określa prawdopodobieństwo, że w objętości znajduje się jedna cząstka dV 1, drugi pod względem objętości dV 2 itd.
Znając zatem funkcję falową układu cząstek, można znaleźć prawdopodobieństwo dowolnej konfiguracji przestrzennej układu mikrocząstek, a także prawdopodobieństwo dowolnej wielkości mechanicznej, zarówno dla układu jako całości, jak i dla pojedynczej cząstki, a także obliczyć średnią wartość wielkości mechanicznej.
Funkcję falową układu cząstek wyznacza się z równania Schrödingera
 , Gdzie
, Gdzie
Operator funkcji Hamiltona dla układu cząstek
 +
+
 .
.

![]() funkcja mocy dla I-
och, cząstki w polu zewnętrznym i
funkcja mocy dla I-
och, cząstki w polu zewnętrznym i
Energia interakcji I- o I J- och cząstki.
Nierozróżnialność identycznych cząstek w kwantze
mechanika
Cząstki o tej samej masie, ładunku elektrycznym, spinie itp. będzie zachowywał się dokładnie tak samo w tych samych warunkach.
Hamiltonian takiego układu cząstek o identycznych masach M oi i identyczne funkcje mocy U i można zapisać w formie przedstawionej powyżej.
Jeśli zmienisz system I- tak i J- y cząstek, to ze względu na identyczność cząstek identycznych stan układu nie powinien się zmieniać. Całkowita energia układu, a także wszystkie wielkości fizyczne charakteryzujące jego stan pozostaną niezmienione.
Zasada identyczności identycznych cząstek: W układzie identycznych cząstek realizowane są tylko takie stany, które nie zmieniają się przy zamianie cząstek.
Stany symetryczne i antysymetryczne
Wprowadźmy operator permutacji cząstek w rozważanym układzie - . Efektem tego operatora jest zamiana I- Wow IJ- y cząstki układu.
Zasada identyczności cząstek identycznych w mechanice kwantowej prowadzi do tego, że wszystkie możliwe stany układu utworzonego przez identyczne cząstki dzielą się na dwa typy:
symetryczny, dla którego
antysymetryczny, dla którego
(X 1 , y 1 ,z 1 … X N , y N , z N , T) = - Ψ A ( X 1 , y 1 ,z 1 … X N , y N , z N , T).
Jeśli funkcja falowa opisująca stan układu jest symetryczna (antysymetryczna) w dowolnym momencie, to ten typ symetrii pozostaje taki sam w każdym innym momencie.
Bozony i fermiony
Cząstki, których stany są opisane symetrycznymi funkcjami falowymi, nazywane są bozony Statystyka Bosego-Einsteina . Bozony obejmują fotony, π- I Do- mezony, fonony w ciałach stałych, ekscytony w półprzewodnikach i dielektrykach. Wszystkie bozony majązero lub spin całkowity .
Cząstki, których stany są opisane antysymetrycznymi funkcjami falowymi, nazywane są fermiony . Układy składające się z takich cząstek są posłuszne Statystyka Fermiego – Diraca . Fermiony obejmują elektrony, protony, neutrony, neutrina i wszystkie cząstki elementarne i antycząstkipół obrotu.
Związek spinu cząstki z rodzajem statystyki pozostaje aktualny w przypadku cząstek złożonych składających się z elementarnych. Jeśli całkowity spin cząstki zespolonej jest równy liczbie całkowitej lub zeru, wówczas cząstka ta jest bozonem, a jeśli jest równy liczbie półcałkowitej, wówczas cząstka jest fermionem.
Przykład: cząstka α() składa się z dwóch protonów i dwóch neutronów, tj. cztery fermiony o spinach +. Zatem spin jądra wynosi 2 i jądro to jest bozonem.
Jądro lekkiego izotopu składa się z dwóch protonów i jednego neutronu (trzech fermionów). Spin tego jądra. Zatem rdzeń jest fermionem.
Zasada Pauliego (wyłączenie Pauliego)
W systemie identycznymfermiony Nie mogą istnieć dwie cząstki w tym samym stanie kwantowym.
W przypadku układu składającego się z bozonów zasada symetrii funkcji falowych nie nakłada żadnych ograniczeń na stany układu. Może być w tym samym stanie dowolną liczbę identycznych bozonów.
Układ okresowy pierwiastków
Na pierwszy rzut oka wydaje się, że w atomie wszystkie elektrony powinny wypełniać poziom o możliwie najniższej energii. Doświadczenie pokazuje, że tak nie jest.
Rzeczywiście, zgodnie z zasadą Pauliego, w atomie Nie może być elektronów o tych samych wartościach wszystkich czterech liczb kwantowych.
Każda wartość głównej liczby kwantowej P odpowiada 2 P 2 stany różniące się od siebie wartościami liczb kwantowych l , M I M S .
Zbiór elektronów w atomie o identycznych wartościach liczb kwantowych P tworzy tak zwaną skorupę. Według numeru P
Muszle dzielą się na podpowłoki, różniących się liczbą kwantową l . Liczba stanów w podpowłoce wynosi 2(2 l + 1).
Różne stany podpowłoki różnią się wartościami liczb kwantowych T I M S .
|
Powłoka |
||||||||||||||
|
Podpowłoka |
||||||||||||||
|
T S |
system składa się z duża liczba identyczny podsystemów, możliwa jest synchronizacja grzejników. kwant przejścia do różnych...klas nie będą emitowane. kwant przejścia tworzą przejścia tunelowe cząsteczki. Tunel kwant przejścia pozwalają opisać... Obliczenie kwant- parametry chemiczne PAS i określenie zależności struktura-aktywność na przykładzie sulfonamidówPraca dyplomowa >> ChemiaXn) - funkcja falowa dla systemy z N cząsteczki, co zależy od ich... przestrzeni. W rzeczywistości elektrony z identyczny za plecami starają się uniknąć niedokładności wyników. sulfonamid kwant chemiczna cząsteczka organiczna Więcej... Chemia ogólna i nieorganicznaPodręcznik do nauki >> ChemiaJednocześnie są dwa elektrony ten sam zestaw czterech kwant kwant liczby (wypełnianie orbitali elektronami... w pobliżu wartości energetycznej E systemy z N cząsteczki. Po raz pierwszy związek między E. a prawdopodobieństwem stanu systemy została założona przez L. Boltzmanna... |
Układ kwantowy
Aby wyjaśnić wiele właściwości mikrocząstek (fotonów, elektronów itp.), potrzebne są specjalne prawa i podejścia mechaniki kwantowej. Kwantowe właściwości mikroświata manifestują się poprzez właściwości makrosystemów. Mikroobiekty tworzą pewien układ fizyczny, który nazywa się kwantowym. Przykładami układów kwantowych są: gaz fotonowy, elektrony w metalach. Zgodnie z warunkami układ kwantowy, cząstka kwantowa należy rozumieć przedmiot materialny, który opisuje się za pomocą specjalnego aparatu mechaniki kwantowej.
Mechanika kwantowa bada właściwości i zjawiska świata mikrocząstek, których mechanika klasyczna nie jest w stanie zinterpretować. Takimi cechami były na przykład: dualizm korpuskularno-falowy, dyskretność i istnienie spinów. Metody mechaniki klasycznej nie są w stanie opisać zachowania cząstek mikroświata. Jednoczesne właściwości falowe i korpuskularne mikrocząstki nie pozwalają na określenie stanu cząstki z klasycznego punktu widzenia.
Fakt ten znajduje odzwierciedlenie w relacji niepewności Heisenberga (1925 $):
gdzie $\trójkąt x$ jest błędem w określeniu współrzędnej, $\trójkąt p$ jest błędem w określeniu pędu mikrocząstki. Zależność tę można zapisać jako:
gdzie $\triangle E$ to niepewność wartości energii, $\triangle t$ to niepewność czasu. Zależności (1) i (2) wskazują, że jeśli jedna z wielkości w tych zależnościach zostanie wyznaczona z dużą dokładnością, to drugi parametr będzie obarczony dużym błędem wyznaczenia. W tych relacjach $\hbar =1,05\cdot (10)^(-34)J\cdot s$. Zatem stanu mikrocząstki w mechanice kwantowej nie można opisać za pomocą jednocześnie współrzędnych i pędu, co jest możliwe w mechanice klasycznej. Podobna sytuacja dotyczy energii w danym momencie. Stany o określonej wartości energii można uzyskać jedynie w przypadkach stacjonarnych (czyli takich, które nie mają dokładnej definicji w czasie).
Mając właściwości korpuskularne i jednocześnie falowe, mikrocząstka nie ma dokładnej współrzędnej, ale jest „rozmazana” w określonym obszarze przestrzeni. Jeśli w określonym obszarze przestrzeni znajdują się dwie lub więcej cząstek, nie jest możliwe ich odróżnienie od siebie, ponieważ niemożliwe jest śledzenie ruchu każdej z nich. Z powyższego wynika, że cząstki są identyczne w mechanice kwantowej.
Niektóre parametry związane z mikrocząstkami przyjmują wartości dyskretne, których mechanika klasyczna nie jest w stanie wyjaśnić. Zgodnie z przepisami i prawami mechaniki kwantowej, oprócz energii układu, moment pędu układu może być dyskretny:
gdzie $l=0,1,2,\kropki $
spin może przyjmować następujące wartości:
gdzie $s=0,\ \frac(1)(2),\ 1,\ \frac(3)(2),\dots $
Rzut momentu magnetycznego na kierunek pola zewnętrznego przyjmuje wartości:
gdzie $m_z$ jest magnetyczną liczbą kwantową, która przyjmuje wartości: $2s+1: s, s-1,...0,...,-(s-1), -s.$
$(\mu )_B$ -- Magneton Bohra.
Aby matematycznie opisać cechy kwantowe wielkości fizycznych, do każdej wielkości przypisany jest operator. Zatem w mechanice kwantowej wielkości fizyczne są reprezentowane przez operatory, a ich wartości są określane przez średnią wartości własnych operatorów.
Stan układu kwantowego
Każdy stan w układzie kwantowym opisuje się za pomocą funkcji falowej. Funkcja ta przewiduje jednak parametry przyszłego stanu układu z pewnym prawdopodobieństwem i niezbyt wiarygodnie, co stanowi zasadniczą różnicę w stosunku do mechaniki klasycznej. Zatem dla parametrów układu funkcja falowa wyznacza wartości probabilistyczne. Taka niepewność i niedokładność przewidywań wywoływała przede wszystkim kontrowersje wśród naukowców.
Mierzone parametry układu kwantowego
Najbardziej globalne różnice między mechaniką klasyczną a mechaniką kwantową polegają na roli pomiaru parametrów badanego układu kwantowego. Problem pomiarów w mechanice kwantowej polega na tym, że badacz próbując zmierzyć parametry mikrosystemu, badacz oddziałuje na ten układ za pomocą makrourządzenia, zmieniając w ten sposób stan samego układu kwantowego. Zatem próbując dokładnie zmierzyć parametr mikroobiektu (współrzędna, pęd, energia) stajemy przed faktem, że sam proces pomiaru zmienia parametry, które staramy się mierzyć, i to w sposób znaczący. W mikrokosmosie nie da się dokonać dokładnych pomiarów. Zgodnie z zasadą nieoznaczoności zawsze będą występować błędy.
W mechanice kwantowej zmienne dynamiczne są reprezentowane przez operatory, więc nie ma sensu mówić o wartościach liczbowych, ponieważ operator określa działanie na wektor stanu. Wynik jest również reprezentowany jako wektor przestrzenny Hilberta, a nie liczba.
Notatka 1
Tylko jeśli wektor stanu jest wektorem własnym operatora zmiennej dynamicznej, wówczas jego działanie na wektor można sprowadzić do mnożenia przez liczbę bez zmiany stanu. W tym przypadku operator zmiennej dynamicznej można powiązać z pojedynczą liczbą równą wartości własnej operatora. W tym przypadku możemy założyć, że zmienna dynamiczna ma określoną wartość liczbową. Wtedy zmienna dynamiczna ma wartość ilościową niezależną od pomiaru.
W przypadku, gdy wektor stanu nie jest wektorem własnym operatora zmiennej dynamicznej, wówczas wynik pomiaru nie staje się jednoznaczny i mówią jedynie o prawdopodobieństwie uzyskania określonej wartości w pomiarze.
Wyniki teorii, które można zweryfikować empirycznie, to prawdopodobieństwo otrzymania zmiennej dynamicznej w pomiarze o dużej liczbie pomiarów dla tego samego wektora stanu.
Główną cechą układu kwantowego jest funkcja falowa, którą wprowadził M. Born. Znaczenie fizyczne najczęściej określa się nie dla samej funkcji falowej, ale dla kwadratu jej modułu, który określa prawdopodobieństwo, że układ kwantowy znajdzie się w danym punkcie przestrzeni w danym momencie. Podstawą mikroświata jest prawdopodobieństwo. Oprócz znajomości funkcji falowej, do opisu układu kwantowego potrzebne są informacje o innych parametrach, np. o parametrach pola, z którym układ oddziałuje.
Procesy zachodzące w mikrokosmosie leżą poza granicami ludzkiej percepcji zmysłowej. W konsekwencji pojęcia i zjawiska, którymi posługuje się mechanika kwantowa, są pozbawione przejrzystości.
Przykład 1
Ćwiczenia: Z jakim minimalnym błędem można wyznaczyć prędkość elektronu i protonu, jeśli znane są współrzędne cząstek z niepewnością wynoszącą 1 $ µm.
Rozwiązanie:
Jako podstawę do rozwiązania problemu wykorzystujemy relację niepewności Heisenberga w postaci:
\[\trójkąt p_x\trójkąt x\ge \hbar \left(1.1\right),\]
gdzie $\triangle x$ to niepewność współrzędnej, $\triangle p_x$ to niepewność rzutu pędu cząstki na oś X. Wielkość niepewności pędu można wyrazić jako:
\[\trójkąt p_x=m\trójkąt v_x\lewy(1,2\prawy).\]
Podstawiając prawą stronę wyrażenia (1.2) zamiast niepewności rzutu pędu w wyrażeniu (1.1), otrzymujemy:
Ze wzoru (1.3) wyrażamy pożądaną niepewność prędkości:
\[\trójkąt v_x\ge \frac(\hbar )(m\trójkąt x)\left(1.4\right).\]
Z nierówności (1.4) wynika, że minimalny błąd wyznaczenia prędkości cząstki jest równy:
\[\trójkąt v_x=\frac(\hbar )(m\trójkąt x).\]
Znając masę elektronu $m_e=9,1\cdot (10)^(-31)kg,$ przeprowadźmy obliczenia:
\[\trójkąt v_(ex)=\frac(1,05\cdot (10)^(-34))(9,1\cdot (10)^(-31)\cdot (10)^(-6) )=1,1\ cdot (10)^2(\frac(m)(s)).\]
masa protonu jest równa $m_p=1,67\cdot (10)^(-27)kg$, obliczmy błąd pomiaru prędkości protonu w danych warunkach:
\[\trójkąt v_(px)=\frac(1,05\cdot (10)^(-34))(1,67\cdot (10)^(-27)\cdot (10)^(-6) )=0,628\ cdot (10)^(-1)(\frac(m)(s)).\]
Odpowiedź:$\triangle v_(ex)=1,1\cdot (10)^2\frac(m)(s),$ $\triangle v_(px)=0,628\cdot (10)^(-1)\frac(m) (s).$
Przykład 2
Ćwiczenia: Jaki jest minimalny błąd pomiaru energii kinetycznej elektronu, jeśli znajduje się on w obszarze o rozmiarze l.
Rozwiązanie:
Jako podstawę do rozwiązania problemu wykorzystujemy relację niepewności Heisenberga w postaci:
\[\triangle p_xl\ge \hbar \to \triangle p_x\ge \frac(\hbar )(l)\left(2.1\right).\]
Z nierówności (2.1) wynika, że minimalny błąd impulsu jest równy:
\[\trójkąt p_x=\frac(\hbar )(l)\lewy(2.2\prawy).\]
Błąd energii kinetycznej można wyrazić jako:
\[\trójkąt E_k=\frac((\left(\triangle p_x\right))^2)(2m)=\frac((\left(\hbar \right))^2)((\left(l\ po prawej))^22\cdot m_e).\]
Odpowiedź:$\triangle E_k=\frac((\left(\hbar \right))^2)((\left(l\right))^22\cdot m_e).$
W pierwszej i drugiej części podręcznika założono, że cząstki tworzące układy makroskopowe podlegają prawom mechaniki klasycznej. Okazało się jednak, że do wyjaśnienia wielu właściwości mikroobiektów zamiast mechaniki klasycznej trzeba posłużyć się mechaniką kwantową. Właściwości cząstek (elektronów, fotonów itp.) w mechanice kwantowej różnią się jakościowo od zwykłych klasycznych właściwości cząstek. Właściwości kwantowe mikroobiektów tworzących dany układ fizyczny przejawiają się także we właściwościach układu makroskopowego.
Jako takie układy kwantowe rozważymy elektrony w metalu, gaz fotonowy itp. W dalszej części pod słowem układ kwantowy lub cząstka będziemy rozumieć pewien obiekt materialny opisany przez aparat mechaniki kwantowej.
Mechanika kwantowa opisuje właściwości i cechy właściwe cząstkom mikroświata, których często nie potrafimy wyjaśnić w oparciu o klasyczne pojęcia. Do takich cech zalicza się na przykład dualizm cząsteczkowo-falowy mikroobiektów w mechanice kwantowej, odkryty i potwierdzony licznymi faktami eksperymentalnymi, dyskretność różnych parametrów fizycznych, właściwości „spinowe” itp.
Szczególne właściwości mikroobiektów nie pozwalają na opisanie ich zachowania konwencjonalnymi metodami mechaniki klasycznej. Na przykład obecność mikrocząstki wykazującej jednocześnie właściwości falowe i korpuskularne
nie pozwala na jednoczesne dokładne zmierzenie wszystkich parametrów określających stan cząstki z klasycznego punktu widzenia.
Fakt ten znajduje odzwierciedlenie w tzw. relacji niepewności, odkrytej w 1925 roku przez Heisenberga, która polega na tym, że niedokładności w wyznaczaniu współrzędnej i pędu mikrocząstki powiązane są zależnością:
Konsekwencją tej zależności jest szereg innych zależności pomiędzy różnymi parametrami, a w szczególności:
![]()
gdzie jest niepewność wartości energii układu i niepewność czasu.
Obie powyższe zależności pokazują, że jeśli jedna z wielkości zostanie wyznaczona z dużą dokładnością, to druga wielkość okaże się wyznaczona z małą dokładnością. Niedokładności wyznacza się tu za pomocą stałej Plancka, która praktycznie nie ogranicza dokładności pomiarów różnych wielkości dla obiektów makroskopowych. Jednak w przypadku mikrocząstek o niskich energiach, małych rozmiarach i pędach dokładność jednoczesnego pomiaru rejestrowanych parametrów nie jest już wystarczająca.
Zatem stanu mikrocząstki w mechanice kwantowej nie można opisać jednocześnie za pomocą współrzędnych i pędów, jak ma to miejsce w mechanice klasycznej (równania kanoniczne Hamiltona). Podobnie nie możemy mówić o wartości energii cząstki w danym momencie. Stany o określonej energii można uzyskać tylko w przypadkach stacjonarnych, tj. nie są one określone precyzyjnie w czasie.
Posiadając właściwości fali korpuskularnej, każda mikrocząstka nie ma absolutnie precyzyjnie określonej współrzędnej, ale wydaje się być „rozmazana” w przestrzeni. Jeśli istnieje pewien obszar przestrzeni składający się z dwóch lub więcej cząstek, nie możemy ich od siebie rozróżnić, ponieważ nie możemy prześledzić ruchu każdej z nich. Oznacza to fundamentalną nierozróżnialność lub tożsamość cząstek w mechanice kwantowej.
Dalej okazuje się, że wielkości charakteryzujące niektóre parametry mikrocząstek mogą zmieniać się jedynie w określonych fragmentach, czyli kwantach, od czego wzięła się nazwa mechanika kwantowa. Tej dyskretności wielu parametrów określających stany mikrocząstek również nie da się opisać w fizyce klasycznej.
Według mechaniki kwantowej oprócz energii układu wartości dyskretne mogą przyjmować moment pędu układu lub spin, moment magnetyczny oraz ich rzuty w dowolnie wybranym kierunku. Zatem kwadrat momentu pędu może przyjmować tylko następujące wartości:
![]()
Spin może przyjmować tylko wartości
![]()
gdzie to może być
Rzut momentu magnetycznego na kierunek pola zewnętrznego może przyjmować wartości
![]()
gdzie jest magneton Bohra i magnetonowa liczba kwantowa, przyjmując wartość:
Aby matematycznie opisać te cechy wielkości fizycznych, każda wielkość fizyczna musiała być powiązana z pewnym operatorem. Dlatego w mechanice kwantowej wielkości fizyczne są reprezentowane przez operatory, a ich wartości są określane jako średnie z wartości własnych operatorów.
Opisując właściwości mikroobiektów, oprócz właściwości i parametrów spotykanych w klasycznym opisie mikrocząstek, konieczne było wprowadzenie nowych, czysto kwantowych parametrów i właściwości. Należą do nich „spin” cząstki, który charakteryzuje jej własny moment pędu, „interakcja wymiany”, zasada Pauliego itp.
Te cechy mikrocząstek nie pozwalają na ich opisanie za pomocą mechaniki klasycznej. W efekcie mikroobiekty opisywane są za pomocą mechaniki kwantowej, która uwzględnia odnotowane cechy i właściwości mikrocząstek.