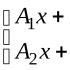Kąt pomiędzy liniami prostymi. Najprostsze zadania z linią prostą na płaszczyźnie

W lipcu 2020 roku NASA rozpoczyna wyprawę na Marsa. Sonda dostarczy na Marsa elektroniczny nośnik z nazwiskami wszystkich zarejestrowanych uczestników wyprawy.

Jeśli ten post rozwiązał Twój problem lub po prostu Ci się spodobał, udostępnij link do niego znajomym w sieciach społecznościowych.

Jedną z tych opcji kodu należy skopiować i wkleić do kodu swojej strony internetowej, najlepiej pomiędzy tagami i/lub bezpośrednio po tagu. Według pierwszej opcji MathJax ładuje się szybciej i mniej spowalnia stronę. Ale druga opcja automatycznie monitoruje i ładuje najnowsze wersje MathJax. Jeśli wstawisz pierwszy kod, będzie on wymagał okresowej aktualizacji. Jeśli wstawisz drugi kod, strony będą ładować się wolniej, ale nie będziesz musiał stale monitorować aktualizacji MathJax.

Najłatwiej połączyć się z MathJax w Bloggerze lub WordPressie: w panelu sterowania witryny dodaj widżet przeznaczony do wstawiania kodu JavaScript innej firmy, skopiuj do niego pierwszą lub drugą wersję kodu pobierania przedstawionego powyżej i umieść widżet bliżej na początek szablonu (nawiasem mówiąc, nie jest to wcale konieczne, ponieważ skrypt MathJax jest ładowany asynchronicznie). To wszystko. Teraz poznaj składnię znaczników MathML, LaTeX i ASCIIMathML i możesz wstawiać formuły matematyczne na stronach internetowych swojej witryny.

Kolejny sylwester... mroźna pogoda i płatki śniegu na szybie... Wszystko to skłoniło mnie do ponownego napisania o... fraktalach i tym, co wie na ten temat Wolfram Alpha. Istnieje ciekawy artykuł na ten temat, który zawiera przykłady dwuwymiarowych struktur fraktalnych. Tutaj przyjrzymy się bardziej złożonym przykładom trójwymiarowych fraktali.

Fraktal można wizualnie przedstawić (opisać) jako figurę geometryczną lub bryłę (co oznacza, że oba są zbiorem, w tym przypadku zbiorem punktów), którego szczegóły mają taki sam kształt jak sama pierwotna figura. Oznacza to, że jest to struktura samopodobna, badając szczegóły, w których powiększeniu zobaczymy ten sam kształt, co bez powiększenia. Natomiast w przypadku zwykłej figury geometrycznej (a nie fraktala) w powiększeniu zobaczymy detale, które mają prostszy kształt niż sama figura pierwotna. Na przykład przy wystarczająco dużym powiększeniu część elipsy wygląda jak odcinek linii prostej. Nie dzieje się tak w przypadku fraktali: przy każdym ich wzroście ponownie zobaczymy ten sam złożony kształt, który będzie się powtarzał przy każdym wzroście.

Benoit Mandelbrot, twórca nauki o fraktalach, napisał w swoim artykule Fractals and Art in the Name of Science: „Fraktale to kształty geometryczne, które są tak samo złożone pod względem szczegółów, jak i ogólnej formy. To znaczy, jeśli stanowią część fraktala zostanie powiększony do rozmiarów całości, pojawi się jako całość, albo dokładnie, albo może z lekkim zniekształceniem.”

Linię prostą w przestrzeni można zawsze zdefiniować jako linię przecięcia dwóch nierównoległych płaszczyzn. Jeżeli równanie jednej płaszczyzny jest równaniem drugiej płaszczyzny, wówczas równanie prostej podaje się jako

Tutaj niewspółliniowy
. Równania te nazywane są równania ogólne prosto w przestrzeń.

Równania kanoniczne prostej

Wektor kierunkowy tej linii nazywa się dowolny niezerowy wektor leżący na danej linii lub do niej równoległy.

Jeśli punkt jest znany
linia prosta i jej wektor kierunkowy
, wówczas równania kanoniczne prostej mają postać:

. (9)

Równania parametryczne prostej

Niech zostaną podane równania kanoniczne prostej

Stąd otrzymujemy równania parametryczne prostej:

(10)

Równania te są przydatne do znajdowania punktu przecięcia linii i płaszczyzny.

Równanie prostej przechodzącej przez dwa punkty
I
ma postać:

Kąt pomiędzy liniami prostymi

równy kątowi między ich wektorami kierunkowymi. Można więc to obliczyć korzystając ze wzoru (4):

Warunek dla prostych równoległych:

Warunek na prostopadłość płaszczyzn:

Odległość punktu od prostej

P powiedzmy, że punkt został podany
i proste

Z równań kanonicznych prostej znamy punkt
, należący do linii i jej wektor kierunkowy
. Następnie odległość punktu
od prostej jest równa wysokości równoległoboku zbudowanego na wektorach I
. Stąd,

Warunek przecięcia linii

Dwie nierównoległe linie

przecinają się wtedy i tylko wtedy, gdy

Względne położenie linii prostej i płaszczyzny.

Niech zostanie podana prosta
i samolot. Narożnik między nimi można znaleźć za pomocą wzoru

Zadanie 73. Napisz równania kanoniczne prostej

(11)

Rozwiązanie. Aby zapisać równania kanoniczne prostej (9), należy znać dowolny punkt należący do tej prostej oraz wektor kierunkowy tej prostej.

Znajdźmy wektor , równolegle do tej linii. Ponieważ musi być prostopadły do wektorów normalnych tych płaszczyzn, tj.

,
, To

Z ogólnych równań prostej mamy to
,
. Następnie

Od tego momentu
dowolny punkt na prostej, wówczas jego współrzędne muszą spełniać równania prostej i można określić jedno z nich, np.
, znajdujemy pozostałe dwie współrzędne z układu (11):

Stąd,
.

Zatem równania kanoniczne pożądanej linii mają postać:

Lub
.

Zadanie 74.

I
.

Rozwiązanie. Z równań kanonicznych pierwszej prostej znane są współrzędne punktu
należące do linii oraz współrzędne wektora kierunku
. Z równań kanonicznych drugiej prostej znane są także współrzędne punktu
i współrzędne wektora kierunku
.

Odległość między liniami równoległymi jest równa odległości punktu
z drugiej prostej. Odległość tę oblicza się ze wzoru

Znajdźmy współrzędne wektora
.

Obliczmy iloczyn wektorowy
:

Zadanie 75. Znajdź punkt punkt symetryczny
stosunkowo proste

Rozwiązanie. Zapiszmy równanie płaszczyzny prostopadłej do danej prostej i przechodzącej przez punkt . Jako jego wektor normalny możesz wziąć wektor kierunkowy linii prostej. Następnie
. Stąd,

Znajdźmy punkt
punkt przecięcia tej prostej i płaszczyzny P. W tym celu zapisujemy równania parametryczne prostej za pomocą równań (10), otrzymujemy

Stąd,
.

Pozwalać
punkt symetryczny do punktu
względem tej linii. Następnie wskaż
punkt środkowy
. Aby znaleźć współrzędne punktu Korzystamy ze wzorów na współrzędne środka odcinka:

,
,
.

Więc,
.

Zadanie 76. Napisz równanie płaszczyzny przechodzącej przez linię
I

a) przez punkt
;

b) prostopadle do płaszczyzny.

Rozwiązanie. Zapiszmy ogólne równania tej prostej. Aby to zrobić, rozważ dwie równości:

Oznacza to, że żądana płaszczyzna należy do wiązki płaszczyzn z generatorami i jej równanie można zapisać w postaci (8):

a) Znajdźmy
I od warunku, że płaszczyzna przechodzi przez punkt
dlatego jego współrzędne muszą spełniać równanie płaszczyzny. Podstawmy współrzędne punktu
do równania wiązki płaszczyzn:

Znaleziono wartość
Podstawmy to do równania (12). otrzymujemy równanie pożądanej płaszczyzny:

b) Znajdźmy
I z warunku, że żądana płaszczyzna jest prostopadła do płaszczyzny. Wektor normalny danej płaszczyzny
, wektor normalny żądanej płaszczyzny (patrz równanie wiązki płaszczyzn (12).

Dwa wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny wynosi zero. Stąd,

Zastąpmy znalezioną wartość
w równanie wiązki płaszczyzn (12). Otrzymujemy równanie pożądanej płaszczyzny:

Problemy do samodzielnego rozwiązania

Zadanie 77. Sprowadź równanie prostych do postaci kanonicznej:

1)
2)

Zadanie 78. Napisz równania parametryczne prostej
, Jeśli:

1)
,
; 2)
,
.

Zadanie 79. Zapisz równanie płaszczyzny przechodzącej przez ten punkt
prostopadle do linii prostej

Zadanie 80. Napisz równania prostej przechodzącej przez punkt
prostopadle do płaszczyzny.

Zadanie 81. Znajdź kąt między liniami:

1)
I
;

2)
I

Zadanie 82. Udowodnij równoległość prostych:

I
.

Zadanie 83. Udowodnij prostopadłość prostych:

Zadanie 84. Oblicz odległość punktu
z linii prostej:

1)
; 2)
.

Zadanie 85. Oblicz odległość między liniami równoległymi:

I
.

Zadanie 86. W równaniach prostej
zdefiniować parametr tak aby ta linia przecinała się z linią i znajdź punkt ich przecięcia.

Zadanie 87. Pokaż, że jest prosto
równolegle do płaszczyzny
i linię prostą
leży w tej płaszczyźnie.

Zadanie 88. Znajdź punkt punkt symetryczny względem samolotu
, Jeśli:

1)
, ;

2)
, ;.

Zadanie 89. Napisz równanie prostopadłej upuszczonej z punktu
bezpośrednio
.

Zadanie 90. Znajdź punkt punkt symetryczny
stosunkowo proste
.

Och, och, och, och… no cóż, jest ciężko, jakby sam sobie czytał zdanie =) Jednak relaks przyda się później, tym bardziej, że dzisiaj kupiłem odpowiednie akcesoria. Przejdźmy zatem do pierwszej części, mam nadzieję, że do końca artykułu utrzymam pogodny nastrój.

Względne położenie dwóch linii prostych

Dzieje się tak, gdy publiczność śpiewa razem z chórem. Dwie linie proste mogą:

1) mecz;

2) być równoległe: ;

3) lub przecinają się w jednym punkcie: .

Pomoc dla manekinów : proszę zapamiętać znak matematyczny skrzyżowania, będzie to miało miejsce bardzo często. Oznaczenie oznacza, że linia przecina się z linią w punkcie .

Jak określić względne położenie dwóch linii?

Zacznijmy od pierwszego przypadku:

Dwie proste pokrywają się wtedy i tylko wtedy, gdy odpowiadające im współczynniki są proporcjonalne, to znaczy istnieje liczba „lambda”, która spełnia równość

Rozważmy linie proste i utwórz trzy równania z odpowiednich współczynników: . Z każdego równania wynika, że zatem te linie się pokrywają.

Rzeczywiście, jeśli wszystkie współczynniki równania pomnóż przez –1 (zmień znak) i wszystkie współczynniki równania po przecięciu przez 2 otrzymasz to samo równanie: .

Drugi przypadek, gdy linie są równoległe:

Dwie linie są równoległe wtedy i tylko wtedy, gdy ich współczynniki zmiennych są proporcjonalne: , Ale .

Jako przykład rozważmy dwie linie proste. Sprawdzamy proporcjonalność odpowiednich współczynników dla zmiennych:

Jednakże jest to całkiem oczywiste.

I trzeci przypadek, gdy linie się przecinają:

Dwie linie przecinają się wtedy i tylko wtedy, gdy ich współczynniki dla zmiennych NIE są proporcjonalne, to znaczy NIE ma takiej wartości „lambda”, którą spełniają równości

Zatem dla prostych stworzymy układ:

Z pierwszego równania wynika, że , a z drugiego równania: , co oznacza system jest niespójny(brak rozwiązań). Zatem współczynniki zmiennych nie są proporcjonalne.

Wniosek: linie się przecinają

W przypadku problemów praktycznych można skorzystać z omówionego właśnie schematu rozwiązania. Nawiasem mówiąc, bardzo przypomina algorytm sprawdzania wektorów pod kątem współliniowości, który oglądaliśmy na zajęciach Pojęcie liniowej (nie)zależności wektorów. Baza wektorów. Ale jest bardziej cywilizowane opakowanie:

Przykład 1

Znajdź względne położenie linii:

Rozwiązanie opiera się na badaniu wektorów kierunku prostych:

a) Z równań znajdujemy wektory kierunkowe linii: .

, co oznacza, że wektory nie są współliniowe, a linie przecinają się.

Na wszelki wypadek postawię na skrzyżowaniu kamień z napisami:

Reszta przeskakuje kamień i podąża dalej, prosto do Nieśmiertelnego Kaszczeja =)

b) Znajdź wektory kierunkowe linii:

Linie mają ten sam wektor kierunkowy, co oznacza, że są równoległe lub pokrywają się. Nie ma tu potrzeby liczenia wyznacznika.

Jest oczywiste, że współczynniki niewiadomych są proporcjonalne, a .

Sprawdźmy, czy równość jest prawdziwa:

Zatem,

c) Znajdź wektory kierunkowe linii:

Obliczmy wyznacznik złożony ze współrzędnych tych wektorów:
dlatego wektory kierunkowe są współliniowe. Linie są równoległe lub pokrywają się.

Współczynnik proporcjonalności „lambda” można łatwo zobaczyć bezpośrednio ze stosunku współliniowych wektorów kierunkowych. Można to jednak również znaleźć na podstawie współczynników samych równań: .

Sprawdźmy teraz, czy równość jest prawdziwa. Obydwa wolne terminy mają wartość zerową, więc:

Wynikowa wartość spełnia to równanie (na ogół spełnia je dowolna liczba).

W ten sposób linie się pokrywają.

Odpowiedź :

Już wkrótce nauczysz się (a nawet już nauczyłeś się), jak rozwiązać problem omawiany ustnie dosłownie w ciągu kilku sekund. W związku z tym nie widzę sensu proponowania czegokolwiek w zamian za samodzielne rozwiązanie, lepiej włożyć w geometryczny fundament kolejną ważną cegłę:

Jak skonstruować prostą równoległą do danej?

Za nieznajomość tego najprostszego zadania Słowik Zbójca surowo karze.

Przykład 2

Linię prostą wyznacza równanie. Napisz równanie prostej równoległej przechodzącej przez ten punkt.

Rozwiązanie: Oznaczmy nieznaną linię literą . Co mówi o niej ten stan? Prosta przechodzi przez ten punkt. A jeśli linie są równoległe, to oczywiste jest, że wektor kierunkowy linii prostej „tse” nadaje się również do zbudowania linii prostej „de”.

Wyciągamy wektor kierunkowy z równania:

Odpowiedź :

Przykładowa geometria wygląda prosto:

Testowanie analityczne składa się z następujących kroków:

1) Sprawdzamy, czy proste mają ten sam wektor kierunkowy (jeśli równanie prostej nie zostanie odpowiednio uproszczone, to wektory będą współliniowe).

2) Sprawdź, czy punkt spełnia otrzymane równanie.

W większości przypadków badania analityczne można łatwo przeprowadzić ustnie. Spójrz na te dwa równania, a wielu z Was szybko określi równoległość linii bez żadnego rysunku.

Przykłady samodzielnych rozwiązań będą dziś kreatywne. Bo nadal będziesz musiał konkurować z Babą Jagą, a ona, jak wiadomo, jest miłośniczką wszelkiego rodzaju zagadek.

Przykład 3

Napisz równanie prostej przechodzącej przez punkt równoległy do prostej jeśli

Istnieje racjonalny i niezbyt racjonalny sposób rozwiązania tego problemu. Najkrótsza droga jest na końcu lekcji.

Pracowaliśmy trochę z liniami równoległymi i wrócimy do nich później. Przypadek zbiegających się linii jest mało interesujący, więc rozważmy problem, który jest Ci dobrze znany ze szkolnego programu nauczania:

Jak znaleźć punkt przecięcia dwóch linii?

Jeśli prosto przecinają się w punkcie , to jego współrzędne są rozwiązaniem układy równań liniowych

Jak znaleźć punkt przecięcia prostych? Rozwiąż system.

Oto geometryczne znaczenie układu dwóch równań liniowych z dwiema niewiadomymi - są to dwie przecinające się (najczęściej) linie na płaszczyźnie.

Przykład 4

Znajdź punkt przecięcia linii

Rozwiązanie: Istnieją dwa sposoby rozwiązania - graficzny i analityczny.

Metoda graficzna polega po prostu na narysowaniu podanych linii i ustaleniu punktu przecięcia bezpośrednio z rysunku:

Oto nasz punkt widzenia: . Aby to sprawdzić należy podstawić jego współrzędne do każdego równania prostej, powinny pasować zarówno tam, jak i tam. Innymi słowy, współrzędne punktu są rozwiązaniem układu. Zasadniczo przyjrzeliśmy się rozwiązaniu graficznemu układy równań liniowych z dwoma równaniami i dwiema niewiadomymi.

Metoda graficzna nie jest oczywiście zła, ale zauważalne są wady. Nie, nie chodzi o to, że siódmoklasiści tak decydują, chodzi o to, że stworzenie prawidłowego i DOKŁADNEGO rysunku zajmie trochę czasu. Poza tym niektóre linie proste nie są tak łatwe do skonstruowania, a sam punkt przecięcia może znajdować się gdzieś w trzydziestym królestwie poza kartką zeszytu.

Dlatego bardziej celowe jest poszukiwanie punktu przecięcia metodą analityczną. Rozwiążmy układ:

Do rozwiązania układu wykorzystano metodę dodawania równań wyraz po wyrazie. Aby rozwinąć odpowiednie umiejętności, weź lekcję Jak rozwiązać układ równań?

Odpowiedź :

Sprawdzenie jest banalne – współrzędne punktu przecięcia muszą spełniać każde równanie układu.

Przykład 5

Znajdź punkt przecięcia prostych, jeśli się przecinają.

To jest przykład, który możesz rozwiązać samodzielnie. Wygodnie jest podzielić zadanie na kilka etapów. Analiza warunku sugeruje, że konieczne jest:
1) Zapisz równanie prostej.
2) Zapisz równanie prostej.
3) Znajdź względne położenie linii.
4) Jeśli linie przecinają się, znajdź punkt przecięcia.

Opracowanie algorytmu działania jest typowe dla wielu problemów geometrycznych i będę się na tym wielokrotnie skupiał.

Pełne rozwiązanie i odpowiedź na końcu lekcji:

Zanim dotarliśmy do drugiej części lekcji, nie zużyła się nawet para butów:

Prostopadłe linie. Odległość punktu od linii.
Kąt pomiędzy liniami prostymi

Zacznijmy od typowego i bardzo ważnego zadania. W pierwszej części nauczyliśmy się budować linię prostą równoległą do tej, a teraz chatka na udkach kurczaka obróci się o 90 stopni:

Jak skonstruować prostą prostopadłą do danej?

Przykład 6

Linię prostą wyznacza równanie. Zapisz równanie prostopadłe do prostej przechodzącej przez ten punkt.

Rozwiązanie: Z warunku wiadomo, że . Byłoby miło znaleźć wektor kierujący linii. Ponieważ linie są prostopadłe, sztuczka jest prosta:

Z równania „usuwamy” wektor normalny: , który będzie wektorem kierującym prostej.

Ułóżmy równanie linii prostej za pomocą punktu i wektora kierunku:

Odpowiedź :

Rozwińmy szkic geometryczny:

Hmmm... Pomarańczowe niebo, pomarańczowe morze, pomarańczowy wielbłąd.

Analityczna weryfikacja rozwiązania:

1) Wyciągamy wektory kierunkowe z równań i z pomocą Iloczyn skalarny wektorów dochodzimy do wniosku, że proste są rzeczywiście prostopadłe: .

Nawiasem mówiąc, możesz użyć normalnych wektorów, jest to jeszcze łatwiejsze.

2) Sprawdź, czy punkt spełnia otrzymane równanie .

Test ponownie można łatwo przeprowadzić ustnie.

Przykład 7

Znajdź punkt przecięcia prostych prostopadłych, jeśli równanie jest znane i okres.

To jest przykład, który możesz rozwiązać samodzielnie. Problem obejmuje kilka działań, dlatego wygodnie jest formułować rozwiązanie punkt po punkcie.

Nasza ekscytująca podróż trwa:

Odległość od punktu do linii

Przed nami prosty pas rzeki i naszym zadaniem jest dotarcie do niego najkrótszą drogą. Nie ma żadnych przeszkód, a najbardziej optymalną trasą będzie poruszanie się po prostopadle. Oznacza to, że odległość punktu od linii to długość odcinka prostopadłego.

Odległość w geometrii tradycyjnie oznacza się grecką literą „rho”, na przykład: – odległość od punktu „em” do prostej „de”.

Odległość od punktu do linii wyrażone wzorem

Przykład 8

Znajdź odległość punktu od linii

Rozwiązanie: wystarczy ostrożnie podstawić liczby do wzoru i wykonać obliczenia:

Odpowiedź :

Zróbmy rysunek:

Znaleziona odległość punktu od linii jest dokładnie równa długości czerwonego odcinka. Jeśli narysujesz rysunek na papierze w kratkę w skali 1 jednostki. = 1 cm (2 komórki), wówczas odległość można zmierzyć zwykłą linijką.

Rozważmy inne zadanie oparte na tym samym rysunku:

Zadanie polega na znalezieniu współrzędnych punktu, który jest symetryczny względem punktu względem prostej . Sugeruję wykonanie kroków samodzielnie, ale przedstawię algorytm rozwiązania z wynikami pośrednimi:

1) Znajdź linię prostopadłą do tej linii.

2) Znajdź punkt przecięcia linii: .

Obydwa działania zostały szczegółowo omówione w tej lekcji.

3) Punkt jest środkiem odcinka. Znamy współrzędne środka i jednego z końców. Przez wzory na współrzędne środka odcinka znaleźliśmy .

Dobrze byłoby sprawdzić, czy odległość wynosi również 2,2 jednostki.

W obliczeniach mogą pojawić się tutaj trudności, ale w wieży dużą pomocą jest mikrokalkulator, pozwalający obliczyć ułamki zwykłe. Doradzałem już wiele razy i będę polecał jeszcze raz.

Jak znaleźć odległość między dwiema równoległymi liniami?

Przykład 9

Znajdź odległość między dwiema równoległymi liniami

To kolejny przykład, który możesz podjąć samodzielnie. Dam ci małą wskazówkę: istnieje nieskończenie wiele sposobów rozwiązania tego problemu. Podsumowanie lekcji na koniec lekcji, ale lepiej spróbować zgadnąć samodzielnie, myślę, że twoja pomysłowość była dobrze rozwinięta.

Kąt między dwiema prostymi

Każdy narożnik jest ościeżem:

W geometrii za kąt pomiędzy dwiema prostymi przyjmuje się MNIEJSZY kąt, z czego automatycznie wynika, że nie może być rozwarty. Na rysunku kąt wskazany przez czerwony łuk nie jest uważany za kąt pomiędzy przecinającymi się liniami. I jego „zielony” sąsiad lub zorientowany przeciwnie kącik „malinowy”.

Jeśli linie są prostopadłe, to dowolny z 4 kątów można przyjąć jako kąt między nimi.

Czym różnią się kąty? Orientacja. Po pierwsze, kierunek, w którym kąt jest „przewijany”, ma fundamentalne znaczenie. Po drugie, kąt zorientowany negatywnie jest zapisywany znakiem minus, na przykład jeśli .

Dlaczego ci to powiedziałem? Wydaje się, że możemy obejść się przy zwykłym pojęciu kąta. Faktem jest, że wzory, dzięki którym znajdziemy kąty, mogą łatwo dać wynik ujemny i nie powinno Cię to dziwić. Kąt ze znakiem minus nie jest gorszy i ma bardzo specyficzne znaczenie geometryczne. Na rysunku dla kąta ujemnego należy wskazać jego orientację strzałką (zgodnie z ruchem wskazówek zegara).

Jak znaleźć kąt między dwiema liniami prostymi? Istnieją dwie działające formuły:

Przykład 10

Znajdź kąt między liniami

Rozwiązanie i metoda pierwsza

Rozważmy dwie linie proste określone równaniami w postaci ogólnej:

Jeśli linie nie są prostopadłe, to zorientowany Kąt między nimi można obliczyć ze wzoru:

Zwróćmy szczególną uwagę na mianownik - dokładnie tak produkt skalarny wektory kierujące prostych:

Jeśli , to mianownik wzoru wyniesie zero, a wektory będą ortogonalne, a proste będą prostopadłe. Dlatego też zgłoszono zastrzeżenie dotyczące nieprostopadłości linii prostych w sformułowaniu.

W związku z powyższym wygodnie jest sformalizować rozwiązanie w dwóch etapach:

1) Obliczmy iloczyn skalarny wektorów kierunkowych prostych:
, co oznacza, że linie nie są prostopadłe.

2) Znajdź kąt między prostymi, korzystając ze wzoru:

Korzystając z funkcji odwrotnej, łatwo jest znaleźć sam kąt. W tym przypadku używamy nieparzystości arcustangens (patrz. Wykresy i własności funkcji elementarnych ):

Odpowiedź :

W Twojej odpowiedzi podajemy wartość dokładną, a także wartość przybliżoną (najlepiej w stopniach i radianach), obliczoną za pomocą kalkulatora.

No cóż, minus, minus, nic wielkiego. Oto ilustracja geometryczna:

Nic dziwnego, że kąt okazał się mieć negatywną orientację, ponieważ w opisie problemu pierwsza liczba jest linią prostą i właśnie od niej rozpoczęło się „odkręcanie” kąta.

Jeśli naprawdę chcesz uzyskać kąt dodatni, musisz zamienić linie, to znaczy wziąć współczynniki z drugiego równania i weź współczynniki z pierwszego równania. Krótko mówiąc, musisz zacząć od bezpośredniego .