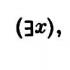Cuantificatori de generalitate și existență. Cuantificatori Sensul formulei logice a predicatelor
1. Cuantificatori.
2. Cuantificator universal.
3. Cuantificator de existență.
4. Conceptul unei formule logice predicate. Sensul formulei
logica predicatelor.
5. Formule echivalente ale logicii predicatelor.
Conceptul de cuantificator
Cuantificator - (din latină quantum - cât), logicoperație cantitativă
zona obiectelor la care se referă expresia,
obtinute ca urmare a utilizarii sale.
În limbajul obișnuit, purtători de astfel de caracteristici
cuvinte precum „toți”, „fiecare”, „unii”,
„există”,
"disponibil",
"orice",
"orice",
„singur”, „mai multe”, „la infinit de multe”,
„număr finit”, precum și toate cantitative
numerale.
Operații pentru predicat
Pentru predicate se introduc două noiîn comparație cu operațiile logice propoziționale:
cuantificator general
cuantificator de existență
Cuantificator general
Fie P(x) un predicat unar definit peset de subiecte M.
O afirmație universală corespunzătoare
predicat P(x), se numește următoarea afirmație:
„fiecare element al multimii M satisface
predicat P(x)"
sau
„pentru fiecare x predicatul este satisfăcut”
Această afirmație se notează - (x)P(x)
Afirmația (x)P(x) este considerată adevărată dacă
predicatul P(x) este identic adevărat și fals
in caz contrar.
Cuantificator general
Simbolul x se numește cuantificatorvariabila x, se citește astfel:
"pentru toate x"
"pentru fiecare x"
"pentru orice x"
comunitatea în
Expresia (x)P(x) spune: „pentru toate x, P(x)”, sau
„pentru fiecare x, P(x).”
De exemplu, x(x=x) este un universal adevărat
afirmație, iar x(x>2) este un universal fals
afirmație.
mulțime finită (a1,a2,...am), atunci:
P(x) P(a1) P(a2) ... P(am)
Cuantificator general
Astfel, cuantificatorul generalpoate fi înțeles ca un operator
conjuncţii prin cuantificabil
variabil.
Cuantificator de existență
Existențialăafirmație,
relevante
predicat
P(x),
numit
afirmația „există un element al mulțimii M,
satisfăcător
predicat
P(x)",
care
se notează cu x P(x) și se consideră adevărată dacă
predicatul P(x) este satisfiabil, dar altfel fals
caz.
Simbolul x se numește cuantificator existențial și
expresia x în care este precedat acest cuantificator
variabila x citește astfel:
„Există x astfel încât...”
"pentru niste x,..."
Cuantificator de existență
DE EXEMPLUx(x>2) – afirmație existențială adevărată
x(x=x+1) este o afirmație existențială falsă.
Dacă P(x) este un predicat unar definit pe
mulţime finită (a1,a2,...am), atunci
P(x) P(a1) P(a2) ... P(am)
Cuantificator de existență
Deci cuantificatorulexistenţa poate fi înţeleasă ca
operator de disjuncţie prin
variabilă cuantificată.
10. Exemple
Exemple de înregistrări de formule și expresiile lor verbale:x(x 2 1 (x 1)(x 1)) Pentru tot x predicatul este satisfăcut...
x(x0)
inegalitate...
x(x0)
Pentru toate x, corect....
y (5 y 5)
Există y astfel încât 5+y=5
y(y 2 y 1 0)
Pentru tot y predicatul este satisfăcut
y(y 2 y 1 0)
Exista tu care....
x(x x)
Pentru unele x, adevărat
3
2
11. Formule ale logicii predicatelor
Logica predicatelor are următorul simbolism:Simbolurile p, q, r, ... sunt variabile propoziționale care iau
două valori: 1 - adevărat, 0 - fals.
Variabilele subiect – x, y, z, …, care rulează
valori dintr-o mulțime M;
x0, y0, z0 – constantele subiectului, adică valorile subiectului
variabile.
P(·), Q(·), F(·), … - variabile predicate unice;
Q(·,·,…,·), R(·,·, …,·) sunt variabile predicate n-are.
P0(·), Q0(·,·, …,·) sunt simboluri ale predicatelor constante.
Simboluri ale operaţiilor logice: , .
Simboluri ale operațiilor cuantificatoare: x, x.
Caractere auxiliare: paranteze, virgule.
12. Formule ale logicii predicatelor
O variabilă subiect se numește liberă dacă aceastanu urmează imediat cuantificatorul și nu este inclus în
domeniul de aplicare al cuantificatorului pe această variabilă, toate celelalte
variabile,
Inbox
V
formulă
sunt numite
conectat.
y z (P(x,y) P(y,z))
Formulele logicii predicatelor sunt:
Fiecare literă de predicat și literă de predicat cu
urmate de variabilele subiectului între paranteze.
Expresii de forma F G, F G, G, F G, F G, (y)F,
(y)G, unde F și G sunt formule logice predicate, variabile
minte.
13. Formule ale logicii predicatelor
Fiecare enunț este atât variabil cât șiconstantă, este o formulă (elementară).
Și
Dacă F(·,·, …,·) este o variabilă predicată n-ară
sau un predicat constant și x1, x2,…, xn sunt obiective
variabile sau constante subiect (nu
sunt neapărat toate distincte), atunci F(x1, x2,…, xn) este
formulă. Această formulă se numește elementară, în
variabilele sale subiect sunt libere, nu
cuantificatori asociati.
14. Formule ale logicii predicatelor
Dacă A și B sunt formule și astfel încât să fie aceleașivariabila subiect nu se află într-una dintre ele
legat și liber în celălalt, apoi cuvintele A B,
A B, A B sunt formule. În aceste formule cei
variabilele care erau în formulele originale
liberi sunt liberi, iar cei care au fost
conectate, sunt conectate.
Dacă A este o formulă, atunci A este o formulă și caracterul
variabilele subiectului în trecerea de la formula A la
formula A nu se modifică.
15. Formule ale logicii predicatelor
Dacă A(x) este o formulă în care subiectulvariabila x intra liber, apoi cuvintele xA(x) si
xA(x) sunt formule, în plus, subiect
variabila este inclusă în ele conectate.
Fiecare cuvânt în afară de cele numite
formulele din paragrafele precedente nu este
formulă.
16. Formule ale logicii predicatelor
De exemplu, dacă P(x) și Q(x,y) sunt singure șipredicate duble și q, r sunt variabile
declarații, atunci formulele vor fi expresii:
q, P(x), P(x) Q(x, y), xP(x) xQ(x, y), (Q(x, y) q) r
0
De exemplu, cuvântul nu este o formulă: xQ(x, y) P(x)
Aici se încalcă condiția clauzei 3, deoarece formula
xQ(x,y) variabila x apare legată, iar în formulă
P(x) variabila x intră liber.
Din definiția formulei logice a predicatului reiese clar că
fiecare formulă de algebră propozițională este
formula logicii predicatelor.
17. Interpretarea formulei predicatului
Interpretarea formulei de calcul predicatse numeşte instanţierea mulţimilor din care
variabilele subiect iau valori și
specificație
relaţii
Și
relevante
seturi de adevăr pentru fiecare literă de predicat.
18. Formule de calcul predicate
identicadevărat la
orice
interpretări,
acestea.
universal valabil
identic
fals
la
orice
interpretări,
acestea.
controversat
fezabil
(formule,
adevăr
care depinde
din
interpretări)
19. Sensul formulei logice a predicatului
Ca exemplu, luați în considerare formulay z (P(x, y) P(y, z))
În formulă, predicatul cu două locuri P(x, y) este definit pe
setați MхM, unde M=(0,1,2,…,n,…), adică MxM=NxN.
Formula include predicatul variabil P(x,y), subiect
variabilele x,y,z, dintre care două y și z sunt conectate prin cuantificatori,
iar x este liber.
Hai sa luam
in spate
specific
sens
predicat
P(x,y)
predicat fix P0(x,y): „x
Apoi, pentru valorile lui y mai mici decât x0=5, predicatul P0(x0,y)
ia valoarea „fals”, iar implicația P(x,y) P(y,z) când
tot z M ia valoarea „adevărat”, adică. afirmație
are sensul „adevărat”.
20. Formule echivalente ale logicii predicatelor
Definiția 1.echivalent pe domeniul M dacă iau
aceleași valori logice pentru toate valorile incluse în
a variabilelor alocate zonei M.
Definiția 2.
Sunt numite două formule logice predicate A și B
echivalente dacă sunt echivalente în orice zonă.
21. Formule echivalente ale logicii predicatelor
Fie A(x) și B(x) predicate variabile, iar C o variabilădeclarație (sau formulă care nu conține x). Apoi au
plasați următoarele echivalențe:
22. Formule echivalente ale logicii predicatelor
ExempluPredicatul Mama(x,y) înseamnă că x este mama lui y.
Atunci y xMama(x,y) înseamnă că fiecare persoană are
mama, este o afirmație adevărată.
x yMama(x,y) înseamnă că există o mamă a tuturor oamenilor, care
este o altă afirmație de al cărui adevăr depinde
seturi de valori pe care y le poate lua: dacă it
multi frati si surori, atunci e adevarat, altfel
in cazul in care este fals.
Astfel, rearanjarea cuantificatorilor universali și
existența poate schimba sensul și sensul unei expresii.
23. Legile operațiilor logice (formule general valabile ale logicii predicatelor)
24. Exercițiu
Găsiți negația următoarelor formule25. Exercițiu
ȘiExercițiu
Demonstrați echivalența
x(A(x) B(x)) xA(x) xB(x)
Fie predicatele A(x) și B(x) să fie identic false. Atunci va fi
fals și predicatul A(x) B(x)
x(A(x) B(x))
În acest caz afirmațiile vor fi false
xA(x) xB(x)
Fie că cel puțin unul dintre predicate (de exemplu, A(x)) nu
identic fals. Atunci nu va fi identic fals și
predicat A(x) B(x)
În acest caz, afirmațiile xA(x) x(A(x) B(x)) vor fi adevărate
Aceasta înseamnă că și formulele originale vor fi adevărate
Prin urmare: x(A(x) B(x)) xA(x) xB(x)
26.
Pe cont propriuPentru un studiu mai detaliat al materialului
citim singuri:
MANUAL: „Logica şi teorie matematică
algoritmi",
autorul Igoshin V.I.
Paginile 157-164
Paginile 165-178
Paginile 178-183
27.
Teme pentru acasăDemonstrați echivalența
C xA(x) x(C A(x))
Demonstrați că formula este general valabilă
A V (P(x) Q(x)) xP(x) xQ(x)
Demonstrați că formula este inconsecventă
A x((F (x) F (x)) (F (x) F (x)))
Natura funcțională a predicatului presupune introducerea unui alt concept - cuantificator. (cuantică – din latină „cât”) Operațiile cuantificatoare pot fi considerate ca o generalizare a operațiilor de conjuncție și disjuncție în cazul regiunilor finite și infinite.
Cuantificator general (toți, toți, toți, orice (toți – „toți”). Expresia verbală corespunzătoare sună astfel:
„Pentru fiecare x P(x) este adevărat.” Apariția unei variabile într-o formulă poate fi legată dacă variabila este situată fie imediat după semnul cuantificatorului, fie în sfera cuantificatorului după care apare variabila. Toate celelalte apariții sunt libere, trecerea de la P(x) la x(Px) sau (Px) se numește legarea variabilei x sau atașarea unui cuantificator la variabila x (sau la predicatul P) sau cuantificarea variabilei x. Se numește variabila la care este atașat cuantificatorul legate de, se numește o variabilă de cuantizare fără legătură gratuit.
De exemplu, variabila x din predicatul P(x) se numește liberă (x este oricare dintre M), în declarația P(x) variabila x este numită variabilă legată.
Echivalența este adevărată: P(x 1)P(x 2)…P(x n),
P(x) – predicat definit pe mulțimea M=(x 1,x 2 ...x 4)
Cuantificator de existență(există – „a exista”). Expresia verbală corespunzătoare este: „Există un x astfel încât P(x) este adevărat”. Enunțul xP(x) nu mai depinde de x, variabila x este conectată printr-un cuantificator.
Echivalența este corectă:
xP(x) = P(x 1)P(x 2)…P(x n), unde
P(x) este un predicat definit pe mulțimea M=(x 1 ,x 2 …x n ).
Cuantificatorul general și cuantificatorul existențial se numesc dual, uneori se folosește notația cuantificatorului! - „există și, în plus, doar unul.”
Este clar că afirmația xP(x) este adevărată numai în cazul unic când P(x) este un predicat identic adevărat, iar afirmația este falsă numai atunci când P(x) este un predicat identic fals.
Operațiile de cuantificare se aplică și predicatelor cu mai multe locuri. Aplicarea unei operații de cuantificare la predicatul P(x,y) în raport cu variabila x pune în corespondență cu predicatul cu două locuri P(x,y) predicatul cu un loc xP(x,y) sau xP( x,y), în funcție de y și independent de x.
La un predicat cu două locuri, puteți aplica operații de cuantificare pe ambele variabile. Apoi obținem opt afirmații:
1. P(x,y); 2. P(x,y);
3. P(x,y); 4. P(x,y);
5. P(x,y); 6. P(x,y);
7. P(x,y); 8. P(x,y)
Exemplul 3. Luați în considerare opțiunile posibile pentru atașarea cuantificatorilor la un predicat P(x,y) – “X impartit de y”, definit pe mulțimea numerelor naturale (fără zero) N. Dați formulări verbale ale afirmațiilor primite și stabiliți-le adevărul.
Operația de atașare a cuantificatorilor conduce la următoarele formule:
Afirmații „pentru oricare două numere naturale, unul este divizibil cu celălalt” (sau 1) toate numerele naturale sunt divizibile cu orice număr natural; 2) orice număr natural este un divizor pentru orice număr natural) fals;
Afirmații „există două numere naturale astfel încât primul este divizibil cu al doilea” (1. „există un număr natural x care este divizibil cu un număr y”; 2. „există un număr natural y care este divizor al lui unele numere naturale x") sunt adevărate;
Afirmația „există un număr natural care este divizibil cu orice număr natural” este falsă;
Afirmația „pentru fiecare număr natural există un număr natural care este divizibil cu primul” (sau pentru fiecare număr natural există un dividend) este adevărată;
Afirmația „pentru fiecare număr natural x există un număr natural y cu care este divizibil” (sau „pentru fiecare număr natural există un divizor”) este adevărată;
Afirmația „există un număr natural care este un divizor al fiecărui număr natural” este adevărată (un astfel de divizor este unul).
În cazul general, schimbarea ordinii cuantificatorilor modifică sensul enunțului și sensul logic al acesteia, i.e. de exemplu, afirmațiile P(x,y) și P(x,y) sunt diferite.
Fie predicatul P(x,y) să însemne că x este mama lui y, atunci P(x,y) înseamnă că fiecare persoană are o mamă - o afirmație adevărată. P(x,y) înseamnă că există o mamă a tuturor oamenilor. Adevărul acestei afirmații depinde de setul de valori pe care îl poți lua: dacă este setul de frați, atunci este adevărat, în caz contrar este fals. Astfel, rearanjarea cuantificatorilor universalității și existenței poate schimba însuși sensul și sensul expresiei.
a) înlocuiți semnul inițial (sau) cu cel opus
b) pune un semn înaintea restului predicatului
Operatorul cu ajutorul căruia aproximativ k.-l. un obiect separat este transformat într-o declarație despre o colecție (set) de astfel de obiecte.
În logică, sunt folosite două coduri de bază: codul generalității, „V” și codul existenței, „E”. În limbajul natural, analogii semantici îndepărtați ai conceptului de comunitate sunt cuvintele „toți”, „oricare”, „toată lumea”; analogi semantici ai existenței K. sunt cuvintele „unii”, „există”. Cu ajutorul datelor K, orice afirmație atributivă de tipul P(x) că un obiect x este inerent în P poate fi transformată într-o declarație cuantificatoare corespunzătoare de tipul VxP(x) și de tipul ZxP(x). În conținut, formula de cuantificare „VxP(x)” în sine se citește ca „pentru tot x există P(x)”, iar formula „ExP(x)” - ca „pentru unele x există P(x)”. O afirmație de forma VxP(x) este adevărată dacă orice x are proprietatea P; și este falsă dacă cel puțin un x nu are proprietatea P. În mod similar, o afirmație de forma ZxP(x) este adevărată dacă cel puțin un x are proprietatea P; și fals dacă niciun x nu are proprietatea P.
Pe baza formulelor cuantificatoare elementare „VxP(x)”, „ExP(x)” pot fi construite alte formule cuantificatoare mai complexe. Relațiile logice dintre astfel de formule sunt studiate în logica predicatelor. În special, formula „ZxP(x)” este echivalentă logic cu formula „) VxQUANTITOR| P(x)”, iar formula „VxP(x)” este echivalentă cu formula „) Eх) P(x)”, unde „)” sunt negații.
Într-o formă implicită, logicile au fost deja folosite de Aristotel, dar în sens strict substantival și formal au fost introduse pentru prima dată în logica lui G. Frege.
Filosofie: Dicţionar Enciclopedic. - M.: Gardariki. Editat de A.A. Ivina. 2004 .
(din lat. cuantic - cât), un operator logic de predicat, aplicat formulelor care conțin o singură variabilă liberă dă (afirmație). Există comunități K., notate prin simbol (din Engleză totul orice), iar K. existenţa (de la a exista - a exista): xP(x) este interpretat (cm. Interpretare) ca „pentru toate x proprietatea P este valabilă”, și xP(x) - ca „există un x astfel încât proprietatea?(x)” să fie valabilă. Dacă (univers) este finit, atunci xP(x) este echivalent cu conjuncția tuturor formulelor P (A), unde a este un element al domeniului subiectului. În mod similar, xP(x) este echivalent cu disjuncția tuturor formulelor de forma? (A). Dacă subiectul este infinit, atunci xP (X)și xP(x) pot fi interpretate ca infinit și, respectiv, disjuncție. Introducere în K. în logica predicatelor multiloc (adică non-singure) determină indecidibilitatea calculului predicat. Diferite relații între principiile generalității și existenței și conexiunile logice ale logicii propoziționale sunt formalizate în calculul predicatului.
Dicționar enciclopedic filozofic. - M.: Enciclopedia Sovietică. Ch. editor: L. F. Ilyichev, P. N. Fedoseev, S. M. Kovalev, V. G. Panov. 1983 .
(din lat. quantum - cât) - logic. operator aplicat la logic. expresii și dând cantități. o caracteristică a domeniului obiectelor (și uneori a domeniului predicatelor), care include ceea ce se obține ca urmare a aplicării lui K. Cât de logic Mijloacele logicii propoziționale nu sunt suficiente pentru a exprima formele judecăților generale, particulare și individuale; în logica predicatelor, obținută prin extinderea logicii propoziționale prin introducerea de principii, astfel de judecăți sunt exprimabile. Deci, de exemplu, patru de bază. forme de judecăţi ale tradiţiilor. logicele „Toți A sunt B”, „Nu A este B”, „Unii A sunt B” și „Unii A nu sunt B” pot fi scrise (dacă ignorăm cerința presupusă a logicii aristotelice pentru non-viditatea lui A). în judecățile generale) folosind simbolismul explicat mai jos, după cum urmează: ∀(x) (A (x) ⊃ B (x)), ∀(x) (A (x) ⊃ B(x)), ∃(x) (A (x ) & B (x)) și ∃ (x) (A (x) & B (x)). Introducere K. vă permite să-l notați într-un mod logic formalizat. limbajul de exprimare al naturii. limbi care conțin cantități. caracteristicile lui k.-l. domeniile subiect sau predicat. În natural În limbi, purtătorii unor astfel de caracteristici sunt așa-numitele. cuvinte cuantificatoare, care includ, în special, cantități. numerale, pronume „toate”, „fiecare”, „unele”, verb „există”, adjective „oricare”, „fiecare”, „singur”, adverbe „la infinit de multe”, etc. Rezultă că pentru a exprima toate cuvintele cuantificatoare menționate într-un formalism. limbaje și logica În calcul, cele două cele mai frecvent utilizate sunt suficiente. K.: K. generalitate (sau în generalitate), notată de obicei prin simbolul ∀ (litera A inversată - litera inițială a cuvântului englezesc „toate”, germană „alle”, etc.), și K. existență, de obicei notată prin simbolul ∃ (litera E inversată este litera inițială a cuvântului englez „exist”, german „existieren”, etc.); semnele ∀ și ∃ în notația unei variabile cuantiale sunt urmate de o literă dintr-un anumit alfabet, numită variabilă cuantificatoare, care este de obicei considerată ca parte a notației unei variabile cuantiale: ∀x, ∀y, ∀F, ∃x, ∃α etc. Pentru generalitățile K. se folosesc și următoarele notații:
pentru K. existența:

Semnul K. se pune înaintea expresiei căreia i se aplică K. (operația de aplicare a K. se numește adesea cuantificare); această expresie este cuprinsă între paranteze (care sunt adesea omise dacă acest lucru nu duce la ambiguitate). Expresia ∀x (A (x)) care conține principiul general se citește ca „Pentru tot x este adevărat că A (x)”, sau „Pentru fiecare x este adevărat că A (x)”; Expresia ∃x (A(x)) care conține K. de existență este citită ca „Există x astfel încât A (x)”, sau „Pentru unele x, A(x) este adevărată.” În ambele cazuri, nu se presupune, în general, că expresia A(x) depinde de fapt de variabila x (s-ar putea să nu conţină deloc variabile, adică poate desemna o anumită afirmaţie; în acest caz, nu schimba sensul acestei afirmatii). Cu toate acestea, principalul scopul lui K. este enunţuri dintr-o expresie care depinde de o variabilă cuantificatoare, sau cel puţin o reducere a numărului de variabile de care depinde această expresie, fiind o formulă deschisă (deschisă) (vezi Formula închisă). De exemplu, expresia (y>0&z>0&x=y-z) conține trei variabile (x, y și z) și devine o afirmație (adevărat sau fals) când k.-l. def. înlocuirea acestor variabile cu numele anumitor obiecte din gama valorilor acestora. Expresia ∃ z(y>0&z>0&x = y-z) depinde doar de două variabile (x și y), iar ∃y∃z (y>0&z>0& &x = y –z) - de un x. Ultima formulă exprimă, așadar, o anumită proprietate (un loc). În cele din urmă, formula ∃х∃у∃z (y>0&z>0&x=y–z) exprimă un afirmație.
Dr. exemple de formule care conțin K.: 1) ∀x(x>0); 2) ∃x(x>0); 3) ∀х (2+2=5); 4) ∃x (2+2=4); 5) ∀x (x = x)& (x+2=y); 6) x ∃y sunt părțile formulei din dreapta lor și domeniul de acțiune al unei formule (x = z⊃x ≠ 0). Apariția unei anumite variabile în semnul unei formule sau în domeniul de acțiune al unei formule care conține această variabilă, se numește apariție legată a unei variabile într-o formulă. În alte cazuri, apariția unei variabile se numește liberă. Aceeași poate apărea într-o anumită formulă într-un loc în o formă legată, iar într-un alt loc - într-un loc liber. Aceasta este, de exemplu, formula 5): primele trei (numărând de la stânga) apariții ale variabilei x din ea sunt conectate, ultima este liberă. Uneori se spune că o variabilă este conectată într-o formulă dată dacă toate aparițiile ei din această formulă sunt conexate. În matematică și logică, orice expresie care conține o variabilă liberă poate fi considerată (într-o abordare informală) deoarece, în sensul obișnuit al cuvântului, aceasta (expresia) depinde de diferite valori ale acestei variabile; dând acestei variabile semnificații diferite (adică, înlocuind toate aparițiile sale libere cu numele unui anumit obiect aparținând gamei de valori ale acestei variabile), obținem semnificații diferite (în general vorbind) ale acestei expresii, în funcție de valoarea a variabilei, adică . din constanta substituită în schimb. În ceea ce privește variabilele legate, expresiile care le încadrează nu depind cu adevărat de ele. De exemplu, expresia ∃x(x = 2y), în funcție de y (care este inclusă în mod liber în ea), este echivalentă cu expresiile ∃z(z = 2y), ∃u(u = 2y), etc. Acest lucru logic expresii din variabilele asociate incluse în acestea se regăsesc în așa-numitele. regula pentru redenumirea variabilelor conexe, postulate sau deduse în dep. logic calcul (vezi variabilă, calcul predicat).
Interpretarea de mai sus a sensului lui K. legată de conținutul de logic. teorii. Cât despre calculele în mod corespunzător. sens (așa-numitele sisteme formale), atunci în ele nu are deloc sens să vorbim despre „sensul” cutare sau cutare calcul, care aici este pur și simplu un anumit simbol al calculului. Întrebarea despre semnificația (sensul) calculului se referă în întregime la domeniul interpretării calculului. În aplicarea lui K. putem vorbi despre cel puțin trei interpretări: clasică, intuiționistă și constructivă, corespunzătoare diferitelor concepte de existență și universalitate în logică și matematică (vezi Intuiționism, Logica constructivă). Atât în calculul predicat clasic, cât și intuiționist (constructiv), metodele de inferență în cazurile în care originalul sau formulele de demonstrat conțin o formulă sunt descrise de același așa-numit calcul de predicate. postulate de cuantificare, de ex. postulatele lui Bernays.
Principiile generalității și existenței nu epuizează tipurile de principii folosite în logică.Principiile extensive sunt așa-numitele. ecuații cuantice limitate de forma ∀xP(x)A(x) sau ∃xQ(x)A(x), în care intervalul de modificare a variabilei cuantificatoare x este „limitat” de unele speciale predicat P(x) (sau Q(x)). K. limitate se reduc la K. de generalitate şi existenţă cu ajutorul urmelor. echivalențe: ∀xP(x)A(x) CUANTITOR ∀x(P(x) ⊃A(x)) și ∃xQ(x)A(x) CUANTITOR ∃x(Q(x)&A(x)). Deseori folosit K. de unicitate ∃!xA(x) („există un x unic astfel încât A(x)”) este exprimat și prin K. de generalitate și existență, de exemplu. deci: xA(x) CUANTITOR ∃xA(x)& ∀y∀z(A(y)&A(z)⊃y=z).
Sunt utilizate și alte tipuri de calcule, care nu sunt acoperite de conceptul de calcul limitat, acestea sunt calcule „numerice” de forma ∃xnA(x) („există exact n x diferite astfel încât A(x)”), folosit în logica intuiționistă a calculului.„cvasiexistență” ∃ xA(x), sau („nu este adevărat că nu există un x astfel încât A(x)”); cu t.zr. clasic în logica Q. de „cvasiexistență” nu este diferit de Q. de existență, în logica intuiționistă propoziția ∃xA(x), care nu spune nimic despre existența unui algoritm pentru găsirea unui astfel de x încât A( x), într-adevăr afirmă doar „cvasi”-ul unui astfel de x și K. infinit ∃x∞A(x) („există infinit de mulți x astfel încât A(x)”). Expresiile care conțin principiile infinitului și termenii numerici pot fi scrise și folosind termenii de generalitate și existență. În calculul predicat extins, coeficienții sunt luați nu numai de variabilele subiect, ci și de variabilele de predicat, i.e. se consideră formule de forma ∃F∀xF(x), ∀Ф∃у(Ф(y)), etc.
Lit.: Gilbert D. și Ackerman V., Fundamentele logicii teoretice, trad. din engleză, M., 1947, p. 81-108; Tarski A., Introducere în logica și metodologia științelor deductive, trad. din engleză, M., 1948, cca. 36-42, 100-102, 120-23; Kleene S.K., Introducere în metamatematică, trad. din engleză, M., 1957, p. 72-80, 130-38; Church A., Introducere în logica matematică, trad. din engleză, vol. 1, p. 42–48; Kuznetsov A.V., Contururile logice ale algoritmului, traducerea din limba rusă standardizată în limbajul informațional-logic, în: Rezumate ale rapoartelor la conferința despre prelucrarea informațiilor, traducerea automată și citirea automată a textului, M., 1961; Mostowski A., Despre o generalizare a cuantificatorilor, „Fundam. math.”, 1957, t. 44, nr. 1, p. 12–36; Hailperin T., A theory of restricted quantification, I–II, „J. Symb. Logic”, 1957, v. 22, nr. 1, p. 19–35, nr. 2, p. 113–29.
Yu. Gastev. Moscova.
Enciclopedie filosofică. În 5 volume - M.: Enciclopedia sovietică. Editat de F. V. Konstantinov. 1960-1970 .
Sinonime:
Vedeți ce este „QUANTITOR” în alte dicționare:
Substantiv, număr de sinonime: 1 operator (24) Dicționar de sinonime ASIS. V.N. Trishin. 2013… Dicţionar de sinonime
cuantificator- - Subiecte de telecomunicații, concepte de bază EN cuantificator... Ghidul tehnic al traducătorului
Cuantificator este un nume general pentru operațiile logice care limitează domeniul de adevăr al unui predicat și creează o declarație. Cel mai des menționat: Cuantificator al universalității (denumirea: , se citește: „pentru toți...”, „pentru fiecare...” sau „fiecare...” ... Wikipedia
Un nume general pentru operațiile logice care folosesc predicatul P(x) pentru a construi o declarație care caracterizează domeniul de adevăr al predicatului P(x). În matematică În logică, cuantificatorul universalității și cuantificatorul existenței sunt cel mai frecvent utilizate. O afirmație înseamnă... ... Enciclopedie matematică
Cuantificator- (din latină quantum cât) simbol folosit pentru a desemna anumite operații ale logicii matematice, în același timp o operație logică care conferă o caracteristică cantitativă a câmpului obiectelor cărora expresia obținută în ... ... Începuturile științelor naturale moderne
Pe lângă operațiile logice cunoscute de noi pentru predicate, se introduc două noi: operația de atașare a cuantificatorilor existenței și generalității.
"pentru toți X" (pentru oricine X, pentru fiecare X) se numește cuantificator general si este desemnat X.
Afirmația „există X" (pentru unii X, cel putin pentru unul X, exista asa ceva X) se numește cuantificator de existență si este desemnat X.
Afirmația „există una și numai una” X„(pentru sens unic X) se numește cuantificator de unicitate : ! X.
De exemplu: „Toți arbuștii sunt plante”. Această afirmație conține un cuantificator general („toate”). Afirmația „există numere care sunt multipli ale 5 „conține un cuantificator existențial („există”).
Pentru a obține o declarație dintr-un predicat multiloc, este necesar să se conecteze fiecare variabilă cu cuantificatori. De exemplu, Dacă P(x;y) este un predicat cu două locuri, atunci (xX) (yY) P(x; y)- afirmație.
Dacă nu fiecare variabilă este conectată printr-un cuantificator, atunci ceea ce se obține nu este o afirmație, ci un predicat în funcție de variabila care nu este conectată printr-un cuantificator. Deci, dacă înainte de predicat P(x;y) pune un cuantificator y, atunci obținem predicatul (yY) P(x; y), în funcție de variabilă X.
Să aflăm care dintre următoarele propoziții sunt enunțuri și care sunt predicate: a) există așa ceva X, Ce x+y = 2;
b) pentru orice XȘi la exista egalitate x + y = y + x.
Soluţie: Să identificăm structura logică a acestor propoziții.
a) Propoziția „Există așa ceva” X, Ce x + y = 2" se poate scrie sub forma (xR) x + y = 2.Întrucât doar variabila x este asociată cu un cuantificator, propoziția în cauză cu două variabile este un predicat.
b) Oferta „pentru orice XȘi la apare x + y = y + x" se poate scrie sub forma : (xR) (yR) x + y = y + x, Unde ambele variabile sunt legate. Prin urmare, această propoziție este o declarație.
Dacă vreo variabilă obiectivă dintr-o formulă nu este asociată cu un cuantificator, atunci este numită variabile libere.
De exemplu: (x) xy=uh. Iată variabila la nu este legat de niciun cuantificator, deci este gratuit. Adevărul unei afirmații date nu depinde de el.
Cuantificatori (x) (x) sunt numite dual reciproc.
Cuantificatorii cu același nume pot fi schimbati, ceea ce nu afectează adevărul afirmației.
De exemplu: (y) (x) x + y = 5. Acest afirmația are același lucru sens, ce si (x) (y) x + y = 5.
Pentru cuantificatori diferiți, o schimbare a ordinii poate duce la o schimbare a adevărului enunțului.
De exemplu: (x) (y) x<у , adică pentru orice număr X mai sunt la- afirmație adevărată.
Să schimbăm cuantificatorii: (x) (y) x
În legătură cu introducerea cuantificatorilor, trebuie luate în considerare următoarele:
1. O formulă logică predicată nu poate conține aceeași variabilă obiectiv, care ar fi legată într-o parte a formulei și liberă în alta.
2. Aceeași variabilă nu poate fi în regiunea cuantificatorilor care sunt duali unul cu celălalt.
Se numește încălcarea acestor condiții coliziune variabilă.
Cum se stabilește valoarea de adevăr a unei afirmații cu un cuantificator?
Pentru a demonstra o afirmație cu un cuantificator general trebuie să vă asigurați că atunci când înlocuiți fiecare dintre valori Xîntr-un predicat P(x) acesta din urmă se transformă într-o afirmație adevărată. Dacă mulțimea X este finită, atunci acest lucru se poate face prin enumerarea tuturor cazurilor; dacă mulțimea X este infinită, atunci este necesar să se efectueze raționamentul într-o formă generală.
Afirmație (x) P(x) false dacă o astfel de valoare poate fi specificată AX, la care P(x) se transformă într-o declarație falsă R(a). De aceea, a infirma o afirmație cu un cuantificator general Este suficient să dau un exemplu.
Afirmație (x) P(x) adevărat dacă o astfel de valoare poate fi specificată AX, la care P(x) se transformă într-o afirmație adevărată R(a). Prin urmare, în ordine verifica adevărul unei afirmații cu un cuantificator existenţă , este suficient să dai un exemplu și astfel să-l dovedești.
Pentru a verifica falsitatea unei afirmatii cu cuantificator existenţă (x) P(x), este necesar să se verifice falsitatea fiecăruia P(x), P(x), …, P(x). Dacă setul X Desigur, acest lucru se poate face prin forță brută. Daca sunt multi X la infinit, atunci este necesar să se efectueze raționamentul într-o formă generală.
Exemple.
1. Găsiți valoarea adevărului „dintre numere” 1, 2, 3, 4 există un număr prim”.
Soluţie: Enunțul conține un cuantificator existențial și, prin urmare, poate fi reprezentat ca o disjuncție de enunțuri: „ 1 - număr prim" sau " 2 - număr prim" sau " 3 - număr prim" sau " 4 - Număr prim". Pentru a dovedi adevărul unei disjuncții, adevărul a cel puțin unei afirmații este suficient, de exemplu, „ 3 este un număr prim care este adevărat. Prin urmare, afirmația inițială este de asemenea adevărată.
2. Să demonstrăm că orice pătrat este dreptunghi.
Soluţie: Enunțul conține un cuantificator general. Prin urmare, poate fi prezentat ca o conjuncție: „pătrat - dreptunghi” și „pătrat - dreptunghi” și „pătrat - dreptunghi”, etc. Deoarece toate aceste afirmații sunt adevărate, atunci conjuncția acestor afirmații este adevărată, prin urmare, propoziția inițială este adevărată.
3. „Orice triunghi este isoscel.” Aceasta este o afirmație falsă. Pentru a verifica acest lucru, este suficient să desenați un triunghi care nu este isoscel.a
Pentru a construi negația unui enunț cu cuantificatori necesar:
1) înlocuiți cuantificatorul de generalitate cu cuantificatorul de existență, iar cuantificatorul de existență cu cuantificatorul de generalitate;
2) înlocuiți predicatul cu negația lui.
Exemplu. Să formulăm o negație pentru următoarele afirmații:
a) toate elementele multimii Z chiar; b) unele verbe răspund la întrebarea „ce să faci?”.
Soluţie: a) Să înlocuim cuantificatorul generalității cu cuantificatorul existenței, iar enunțul lui cu negația lui: unele elemente ale mulțimii Z ciudat.
b) Să înlocuim cuantificatorul existenței cu un cuantificator al generalității, iar expresia lui cu negație: toate verbele nu răspund la întrebarea „ce să faci?”
Predicat (lat. praedicatum- afirmat, menționat, spus) - orice enunț matematic în care există cel puțin o variabilă. Predicatul este obiectul principal de studiu în logica de ordinul întâi.
Un predicat este o expresie cu variabile logice care au sens pentru orice valori permise ale acestor variabile.
Expresii: x > 5, x > y – predicate.
predicat ( n-local, sau n-ary) este o funcție cu un set de valori (0,1) (sau „fals” și „adevărat”), definite pe mulțime. Astfel, fiecare set de elemente ale multimii M caracterizat fie ca „adevărat”, fie „fals”.
Un predicat poate fi asociat cu o relație matematică: dacă n-ka aparține relației, atunci predicatul va returna pe ea 1. În special, un predicat unar definește relația de apartenență la o anumită mulțime.
Un predicat este unul dintre elementele logicii de ordinul întâi și superior. Pornind de la logica de ordinul doi, cuantificatorii pot fi plasați pe predicate în formule.
Predicatul este numit identic adevărat si scrie:
dacă pe orice set de argumente ia valoarea 1.
Predicatul este numit identic fals si scrie:
dacă pe orice set de argumente ia valoarea 0.
Predicatul este numit fezabil, dacă ia valoarea 1 pe cel puțin un set de argumente.
Deoarece predicatele au doar două semnificații, toate operațiile algebrei booleene le sunt aplicabile, de exemplu: negație, implicație, conjuncție, disjuncție etc.
Cuantificator este un nume general pentru operațiile logice care limitează domeniul de adevăr al unui predicat. Cel mai des menționat:
Cuantificator universal(denumirea: citește: „pentru toți...”, „pentru toată lumea...” sau „fiecare...”, „oricare...”, „pentru orice...”).
Cuantificator de existență(denumirea: , citește: „există...” sau „va fi găsit...”).
Exemple
Să notăm P(X) predicat " X divizibil cu 5." Folosind cuantificatorul general, putem scrie formal următoarele afirmații (false, desigur):
orice număr natural este divizibil cu 5;
fiecare număr natural este un multiplu al lui 5;
toate numerele naturale sunt multipli ai lui 5;
in felul urmator:
![]() .
.
Următoarele afirmații (deja adevărate) folosesc cuantificatorul existențial:
există numere naturale care sunt multipli ai lui 5;
există un număr natural care este multiplu al lui 5;
cel puțin un număr natural este divizibil cu 5.
Notația lor formală:
![]() .Introducere în concept
.Introducere în concept
Fie predicatul P(x) dat pe mulțimea X de numere prime: „Numărul prim x este impar”. Să înlocuim cuvântul „oricare” în fața acestui predicat. Obținem afirmația falsă „orice număr prim x este impar” (această afirmație este falsă, deoarece 2 este un număr prim par).
Înlocuind cuvântul „există” în fața predicatului dat P(x), obținem afirmația adevărată „Există un număr prim x care este impar” (de exemplu, x = 3).
Astfel, puteți transforma un predicat într-un enunț punând în fața predicatului cuvintele „totul”, „există”, etc., numite cuantificatori în logică.
Cuantificatori în logica matematică
Declarația înseamnă că intervalul variabilei X incluse în domeniul adevărului predicatului P(X).
("Pentru toate valorile lui (x), afirmația este adevărată.")
Afirmația înseamnă că domeniul de adevăr al predicatului P(X) nu este gol.
(„Există un (x) pentru care afirmația este adevărată”).
Întrebarea 31 Graficul și elementele sale. Noțiuni de bază. Incidență, multiplicitate, buclă, contiguitate. Tipuri de grafice. Traseul din grafic și lungimea acestuia. Clasificarea rutelor. Matrici de adiacență ale graficelor direcționate și nedirecționate.
În teoria grafurilor matematice și în informatică, un graf este o colecție de un set nevid de vârfuri și un set de perechi de vârfuri.
Obiectele sunt reprezentate ca vârfuri sau noduri ale unui graf, iar conexiunile sunt reprezentate ca arce sau muchii. Pentru diferite domenii de aplicare, tipurile de grafice pot diferi în direcționalitate, restricții privind numărul de conexiuni și date suplimentare despre vârfuri sau muchii.
O cale (sau lanț) într-un graf este o succesiune finită de vârfuri în care fiecare vârf (cu excepția ultimului) este conectat la următorul din succesiunea de vârfuri printr-o muchie.
O cale direcționată într-un digraf este o succesiune finită de vârfuri v i, pentru care toate perechile ( v i,v i+ 1) sunt muchii (orientate).
Un ciclu este o cale în care primul și ultimul vârf coincid. În acest caz, lungimea unei căi (sau a unui ciclu) este numărul componentelor sale coaste. Rețineți că dacă vârfurile uȘi v sunt capetele unei muchii, apoi, conform acestei definiții, secvența ( u,v,u) este un ciclu. Pentru a evita astfel de cazuri „degenerate”, sunt introduse următoarele concepte.
O cale (sau ciclu) se numește simplu dacă marginile sale nu se repetă; elementar dacă este simplu și vârfurile sale nu se repetă. Este ușor să vezi că:
Fiecare cale care leagă două vârfuri conține o cale elementară care leagă aceleași două vârfuri.
Orice simplu neelementare calea conține elementare ciclu.
Orice simplu un ciclu care trece printr-un vârf (sau muchie) conține elementar(sub-)ciclu care trece prin același vârf (sau muchie).
O buclă este un ciclu elementar.
Grafic sau grafic nedirecționat G este o pereche ordonată G: = (V,E
V
E acesta este un set de perechi (în cazul unui graf nedirecționat, neordonat) de vârfuri, numite muchii.
V(prin urmare E, altfel ar fi un multiset) sunt de obicei considerate multimi finite. Multe rezultate bune obținute pentru grafice finite nu sunt adevărate (sau diferă într-un fel) pentru grafice infinite. Acest lucru se datorează faptului că o serie de considerații devin false în cazul mulțimilor infinite.
Vârfurile și muchiile unui graf se mai numesc și elemente de graf, numărul de vârfuri din graf | V| - ordinea, numărul muchiilor | E| - dimensiunea graficului.
Vârfurile uȘi v sunt numite vârfuri terminale (sau pur și simplu capete) ale unei muchii e = {u,v). O muchie, la rândul său, leagă aceste vârfuri. Două vârfuri ale aceleiași muchii sunt numite adiacente.
Se spune că două muchii sunt adiacente dacă au un vârf comun de capăt.
Două muchii sunt numite multiple dacă mulțimile vârfurilor lor de capăt coincid.
O muchie se numește buclă dacă capetele ei coincid, adică e = {v,v}.
grad deg V culmi V apelați numărul de muchii incidente cu acesta (în acest caz, buclele sunt numărate de două ori).
Se spune că un vârf este izolat dacă nu este capătul vreunei muchii; agățat (sau frunză) dacă este capătul exact al unei margini.
Grafic direcționat (digraf abreviat) G este o pereche ordonată G: = (V,A), pentru care sunt îndeplinite următoarele condiții:
V este un set nevid de vârfuri sau noduri,
A este un set de perechi (ordonate) de vârfuri distincte, numite arce sau muchii direcționate.
Arc este o pereche ordonată de vârfuri (v, w), unde este vârful v numit începutul și w- capătul arcului. Putem spune că arcul duce de sus vîn partea de sus w.
Grafic mixt
Grafic mixt G este un grafic în care unele muchii pot fi direcționate și altele pot fi nedirecționate. Scris ca un triplu comandat G: = (V,E,A), Unde V, EȘi A definit la fel ca mai sus.
Graficele direcționate și nedirecționate sunt cazuri speciale de grafice mixte.
Grafice izomorfe(?)
Grafic G se numește izomorf la grafic H, dacă există o bijecție f din mulţimea vârfurilor graficului G la setul de vârfuri ale graficului H, care are următoarea proprietate: dacă în grafic G există o muchie de la vârf Aîn partea de sus B, apoi în grafic H f(A) în partea de sus f(B) și invers - dacă în grafic H există o muchie de la vârf Aîn partea de sus B, apoi în grafic G trebuie să existe o muchie de la vârf f − 1 (A) în partea de sus f − 1 (B). În cazul unui graf direcționat, această bijecție trebuie să păstreze și orientarea muchiei. În cazul unui grafic ponderat, bijecția trebuie să păstreze și greutatea muchiei.
Graficul matricei adiacentei G cu un număr finit de vârfuri n(numerotate de la 1 la n) este o matrice pătrată A mărimea n, în care valoarea elementului a ij egal cu numărul muchiilor de la i al-lea vârf al graficului în j-al-lea vârf.
Uneori, mai ales în cazul unui graf nedirecționat, o buclă (o muchie de la i al-lea vârf în sine) este numărat ca două muchii, adică valoarea elementului diagonal a iiîn acest caz egal cu dublul numărului de bucle din jur i vârful.
Matricea de adiacență a unui grafic simplu (care nu conține bucle sau muchii multiple) este o matrice binară și conține zerouri pe diagonala principală.
Întrebarea 32 Funcția. Metode de atribuire. Clasificarea funcțiilor. Funcții elementare de bază și grafice ale acestora. Compoziția funcțiilor. Funcții elementare.
Funcția este un concept matematic care reflectă relația dintre elementele mulțimilor. Putem spune că o funcție este o „lege” conform căreia fiecare element dintr-o mulțime (numit domeniul definirii ) este pus în corespondență cu un element al altui set (numit intervalul de valori ).
Conceptul matematic al unei funcții exprimă ideea intuitivă a modului în care o cantitate determină complet valoarea unei alte mărimi. Deci valoarea variabilei X definește în mod unic sensul unei expresii X 2, iar valoarea lunii determină în mod unic valoarea lunii următoare, de asemenea, orice persoană poate fi comparată cu o altă persoană - tatăl său. În mod similar, un algoritm preconceput produce anumite date de ieșire pe baza datelor de intrare variabile.
Metode pentru specificarea unei funcții
Metoda analitica
O funcție este un obiect matematic care este o relație binară care îndeplinește anumite condiții. O funcție poate fi specificată direct ca un set de perechi ordonate, de exemplu: există o funcție . Cu toate acestea, această metodă este complet nepotrivită pentru funcții pe mulțimi infinite (care sunt funcțiile reale obișnuite: putere, liniară, exponențială, logaritmică etc.).
Pentru a specifica o funcție, utilizați expresia: . în care, X este o variabilă care trece prin domeniul de definire al funcției și y- gama de valori. Această intrare indică prezența unei relații funcționale între elementele mulțimilor. XȘi y poate rula prin orice set de obiecte de orice natură. Acestea pot fi numere, vectori, matrici, mere, culori ale curcubeului. Să explicăm cu un exemplu:
Să fie un set mar, avion, para, scaunși multe om, locomotivă, pătrat. Să definim funcția f după cum urmează: (măr, persoană), (avion, locomotivă), (pare, pătrat), (scaun, persoană). Dacă introducem o variabilă x care trece prin mulțime și o variabilă y care trece prin mulțime, funcția specificată poate fi specificată analitic ca: .
Funcțiile numerice pot fi specificate în mod similar. De exemplu: unde x trece prin mulțimea numerelor reale și definește o funcție f. Este important să înțelegeți că expresia în sine nu este o funcție. O funcție ca obiect este un set de (perechi ordonate). Și această expresie ca obiect este egalitatea a două variabile. Definește o funcție, dar nu este una.
Cu toate acestea, în multe ramuri ale matematicii, este posibil să se noteze cu f(x) atât funcția în sine, cât și expresia analitică care o definește. Această convenție sintactică este extrem de convenabilă și justificată.
Metoda grafică
Funcțiile numerice pot fi specificate și folosind un grafic. Fie o funcție reală a n variabile.
Să considerăm un spațiu liniar (n+1)-dimensional peste câmpul numerelor reale (deoarece funcția este reală). Să alegem orice bază () în acest spațiu. Fiecare punct al funcției este asociat cu un vector: . Astfel, vom avea un set de vectori spațiali liniari corespunzători punctelor unei funcții date conform regulii specificate. Punctele spațiului afin corespunzător vor forma o anumită suprafață.
Dacă luăm spațiul euclidian al vectorilor geometrici liberi (segmente direcționate) ca spațiu liniar, iar numărul de argumente al funcției f nu depășește 2, setul specificat de puncte poate fi reprezentat vizual sub forma unui desen (grafic ). Dacă, în plus, se consideră că baza inițială este ortonormală, obținem definiția „școală” a graficului unei funcții.
Pentru funcțiile de 3 sau mai multe argumente, această reprezentare nu este aplicabilă din cauza lipsei de intuiție geometrică a spațiilor multidimensionale a unei persoane.
Cu toate acestea, pentru astfel de funcții se poate veni cu o reprezentare vizuală semi-geometrică (de exemplu, fiecare valoare a celei de-a patra coordonate a unui punct poate fi asociată cu o anumită culoare pe grafic)
Cantitati proportionale. Dacă variabilele yȘi x sunt direct proporționale
y = k x ,

Unde k- valoare constantă ( factor de proporționalitate).
Programa proporționalitate directă– o linie dreaptă care trece prin originea coordonatelor și formează o linie cu axa X unghi a cărui tangentă este egală cu k: bronz = k(Fig. 8). Prin urmare, se mai numește și coeficientul de proporționalitate pantă. Figura 8 prezintă trei grafice pentru k = 1/3, k= 1 și k = 3 .
Funcție liniară. Dacă variabilele yȘi X sunt legate prin ecuația de gradul I:
A x + B y = C ,
unde cel puțin unul dintre numere A sau B nu este egal cu zero, atunci graficul acestei dependențe funcționale este linie dreapta. Dacă C= 0, atunci trece prin origine, altfel nu. Grafice ale funcțiilor liniare pentru diverse combinații A,B,C sunt prezentate în Fig.9.

Proporționalitate inversă. Dacă variabilele yȘi x sunt invers proporționale, atunci relația funcțională dintre ele este exprimată prin ecuația:
y = k / X,
Unde k- valoare constantă.
 Graficul invers proporțional – hiperbolă(Fig. 10). Această curbă are două ramuri. Hiperbolele se obțin atunci când un con circular se intersectează cu un plan (pentru secțiuni conice, vezi secțiunea „Con” din capitolul „Stereometrie”). După cum se arată în Fig. 10, produsul coordonatelor punctelor hiperbolei este o valoare constantă, în exemplul nostru egală cu 1. În cazul general, această valoare este egală cu k, care rezultă din ecuația hiperbolei: xy = k.
Graficul invers proporțional – hiperbolă(Fig. 10). Această curbă are două ramuri. Hiperbolele se obțin atunci când un con circular se intersectează cu un plan (pentru secțiuni conice, vezi secțiunea „Con” din capitolul „Stereometrie”). După cum se arată în Fig. 10, produsul coordonatelor punctelor hiperbolei este o valoare constantă, în exemplul nostru egală cu 1. În cazul general, această valoare este egală cu k, care rezultă din ecuația hiperbolei: xy = k.
Principalele caracteristici și proprietăți ale unei hiperbole:
X 0, interval: y 0 ;
Funcția este monotonă (descrescătoare) la X< 0 și la x> 0, dar nu
per total monoton datorită punctului de rupere X = 0);
Funcție nemărginită, discontinuă într-un punct X= 0, impar, neperiodic;
- Funcția nu are zerouri.
Funcția pătratică. Aceasta este funcția: y = topor 2 + bx + c, Unde a, b, c- permanent, A b=c= 0 și y = topor 2. Graficul acestei funcții parabolă pătrată - OY, Care e numit axa parabolei.Punct O vârful parabolei.

Funcția pătratică. Aceasta este funcția: y = topor 2 + bx + c, Unde a, b, c- permanent, A 0. În cel mai simplu caz avem: b=c= 0 și y = topor 2. Graficul acestei funcții parabolă pătrată - o curbă care trece prin originea coordonatelor (Fig. 11). Fiecare parabolă are o axă de simetrie OY, Care e numit axa parabolei.Punct O se numește intersecția unei parabole cu axa ei vârful parabolei.
Graficul unei funcții y = topor 2 + bx + c- de asemenea o parabolă pătrată de același tip ca y = topor 2, dar vârful său nu se află la origine, ci într-un punct cu coordonate:

Forma și locația unei parabole pătrate în sistemul de coordonate depinde în întregime de doi parametri: coeficientul A la X 2 și discriminant D:D=b 2 – 4ac. Aceste proprietăți rezultă din analiza rădăcinilor unei ecuații pătratice (vezi secțiunea corespunzătoare din capitolul „Algebră”). Toate cazurile diferite posibile pentru o parabolă pătrată sunt prezentate în Fig. 12.
 Principalele caracteristici și proprietăți ale unei parabole pătrate:
Principalele caracteristici și proprietăți ale unei parabole pătrate:
Domeniul de aplicare: < X+ (adică X R), și zona
valori: … (Vă rugăm să răspundeți singur la această întrebare!);
Funcția în ansamblu nu este monotonă, ci la dreapta sau la stânga vârfului
se comportă ca monoton;
Funcția este nelimitată, continuă peste tot, chiar și atunci când b = c = 0,
și neperiodică;
- la D< 0 не имеет нулей.
 Functie exponentiala. Funcţie y = un x, Unde A- se numește un număr constant pozitiv functie exponentiala.Argument X acceptă orice valori valide; funcțiile sunt considerate valori numai numere pozitive, deoarece altfel avem o funcție cu mai multe valori. Da, funcția y = 81X are la X= 1/4 patru valori diferite: y = 3, y = 3, y = 3 iȘi y = 3 i(Nota, vă rog!). Dar considerăm ca fiind valoarea funcției numai y= 3. Grafice ale funcției exponențiale pt A= 2 și A= 1/2 sunt prezentate în Fig. 17. Ele trec prin punctul (0, 1). La A= 1 avem un grafic al unei drepte paralele cu axa X, adică funcţia se transformă într-o valoare constantă egală cu 1. Când A> 1 funcția exponențială crește, iar la 0< A < 1 – убывает. Основные характеристики и свойства показательной функции:
Functie exponentiala. Funcţie y = un x, Unde A- se numește un număr constant pozitiv functie exponentiala.Argument X acceptă orice valori valide; funcțiile sunt considerate valori numai numere pozitive, deoarece altfel avem o funcție cu mai multe valori. Da, funcția y = 81X are la X= 1/4 patru valori diferite: y = 3, y = 3, y = 3 iȘi y = 3 i(Nota, vă rog!). Dar considerăm ca fiind valoarea funcției numai y= 3. Grafice ale funcției exponențiale pt A= 2 și A= 1/2 sunt prezentate în Fig. 17. Ele trec prin punctul (0, 1). La A= 1 avem un grafic al unei drepte paralele cu axa X, adică funcţia se transformă într-o valoare constantă egală cu 1. Când A> 1 funcția exponențială crește, iar la 0< A < 1 – убывает. Основные характеристики и свойства показательной функции:
Domeniul de aplicare: < X+ (adică X R);
gamă: y> 0 ;
Funcția este monotonă: crește cu A> 1 și scade la 0< A < 1;
- Funcția nu are zerouri.
 Funcția logaritmică. Funcţie y=log un x, Unde A– se numește un număr pozitiv constant care nu este egal cu 1 logaritmică. Această funcție este inversul funcției exponențiale; graficul său (Fig. 18) poate fi obținut prin rotirea graficului funcției exponențiale în jurul bisectoarei primului unghi de coordonate.
Funcția logaritmică. Funcţie y=log un x, Unde A– se numește un număr pozitiv constant care nu este egal cu 1 logaritmică. Această funcție este inversul funcției exponențiale; graficul său (Fig. 18) poate fi obținut prin rotirea graficului funcției exponențiale în jurul bisectoarei primului unghi de coordonate.
Principalele caracteristici și proprietăți ale funcției logaritmice:
Domeniul de aplicare: X> 0 și interval de valori: < y+
(adică y R);
Aceasta este o funcție monotonă: crește pe măsură ce A> 1 și scade la 0< A < 1;
Funcția este nelimitată, continuă peste tot, neperiodică;
Funcția are un zero: X = 1.
Funcții trigonometrice. Când construim funcții trigonometrice folosim radian masura unghiurilor.Apoi functia y= păcat X este reprezentată printr-un grafic (Fig. 19). Această curbă se numește sinusoid.

Graficul unei funcții y=cos X prezentat în Fig. 20; aceasta este, de asemenea, o undă sinusoidală rezultată din deplasarea graficului y= păcat X de-a lungul axei X la stânga prin 2

Din aceste grafice, caracteristicile și proprietățile acestor funcții sunt evidente:
Domeniu: < X+ interval de valori: 1 y +1;
Aceste funcții sunt periodice: perioada lor este 2;
Funcții limitate (| y| , continuă peste tot, nu monotonă, dar
având așa-zis intervale de monotonie, in interiorul caruia se afla
se comportă ca funcții monotone (vezi graficele din Fig. 19 și Fig. 20);
Funcțiile au un număr infinit de zerouri (pentru mai multe detalii, vezi secțiunea
„Ecuații trigonometrice”).
Grafice de funcții y= bronzat XȘi y=cot X sunt prezentate în Fig. 21, respectiv Fig. 22.

Din grafice este clar că aceste funcții sunt: periodice (perioada lor ,
nelimitat, în general nu monoton, dar au intervale de monotonitate
(care?), discontinue (ce puncte de discontinuitate au aceste funcții?). Regiune
definițiile și intervalul de valori ale acestor funcții:
Funcții y= Arcin X(Fig.23) și y= Arccos X(Fig. 24) multivaloric, nelimitat; domeniul lor de definire și, respectiv, domeniul de valori: 1 X+1 și < y+ . Deoarece aceste funcții au mai multe valori, nu
considerate în matematica elementară, principalele lor valori sunt considerate funcții trigonometrice inverse: y= arcsin XȘi y= arccos X; graficele lor sunt evidențiate în Fig. 23 și Fig. 24 cu linii groase.
Funcții y= arcsin XȘi y= arccos X au următoarele caracteristici și proprietăți:
Ambele funcții au același domeniu de definiție: 1 X +1 ;
intervalul lor de valori: /2 y/2 pentru y= arcsin X si 0 y Pentru y= arccos X;
(y= arcsin X– functie de crestere; y= arccos X - in scadere);
Fiecare funcție are un zero ( X= 0 pentru funcție y= arcsin XȘi
X= 1 pentru funcție y= arccos X).

Funcții y= Arctan X(Fig.25) și y= Arccot X(Fig. 26) - funcții multi-valorice, nelimitate; domeniul lor de definire: X+ . Principalele lor semnificații y= arctan XȘi y= arccot X sunt considerate funcții trigonometrice inverse; graficele lor sunt evidențiate în Fig. 25 și Fig. 26 cu ramuri aldine.
Funcții y= arctan XȘi y= arccot X au următoarele caracteristici și proprietăți:
Ambele funcții au același domeniu de definiție: X + ;
intervalul lor de valori: /2<y < /2 для y= arctan X si 0< y < для y= arccos X;
Funcțiile sunt limitate, neperiodice, continue și monotone
(y= arctan X– functie de crestere; y= arccot X - in scadere);
Doar funcție y= arctan X are un singur zero ( X= 0);
funcţie y= arccot X nu are zerouri.
Compoziția funcțiilor
Dacă sunt date două hărți și , unde , atunci „harta de la capăt la capăt” de la , dată de formula , are sens, care se numește compoziția funcțiilor și și se notează cu .

Fig. 1.30 Afișare de la capăt la capăt de la până la