Які ознаки рівності трикутників. Перша ознака рівності трикутників

Геометрична фігура, сформована трьома відрізками, які з'єднують три точки, що не належать до однієї прямої.

Сторони трикутника формують у вершинах трикутника три кути. Перефразовуючи, трикутник- це багатокутник, у якого три кути .

Практичне значення ознак рівності трикутниківзводиться до наступного: згідно з формулюванням трикутники рівні, якщо виходить їх накласти один на одного так, щоб вони збіглися; проте реалізувати накладання трикутників іноді буває важко, інколи ж і неможливо.

Ознаки рівності трикутників дозволяють замінити накладання трикутників знаходженням та зіставленням окремих основних компонентів (сторін і кутів) і таким чином обґрунтувати рівність трикутників.

3. Усі три сторони:

Ще виділяють четверта ознака, який не так широко освітлений у шкільному курсі математики, як попередні три. Він формулюється так:

Якщо дві сторони першого трикутника відповідно дорівнюють двом сторонам другого трикутника і кут, що протилежить більшій із цих сторін у першому трикутнику, дорівнює куту, що протилежить відповідно до рівної їй стороні у другому трикутнику, то ці трикутники рівні.

Ознаки рівності трикутників

Рівними називають трикутники, які мають відповідні сторони рівні.

Теорема (перша ознака рівності трикутників).
Якщо дві сторони та кут, укладений між ними, одного трикутника відповідно дорівнюють двом сторонам та кутку, укладеному між ними, іншого трикутника, то такі трикутники рівні.

Теорема (друга ознака рівності трикутників).
Якщо сторона і два прилеглих до неї кута одного трикутника відповідно дорівнюють стороні та двох прилеглих до неї кутів іншого трикутника, то такі трикутники рівні.

Теорема (третя ознака рівності трикутників).
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.

Ознаки подоби трикутників

Подібними називаються трикутники, у яких кути рівні, а подібні сторони пропорційні: , , де - Коефіцієнт подоби.

I ознака подоби трикутників.Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то ці трикутники подібні.

ІІ ознака подоби трикутників.Якщо три сторони одного трикутника пропорційні трьом сторонам іншого трикутника, такі трикутники подібні.

ІІІ ознака подоби трикутників.Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника, а кути, укладені між цими сторонами, рівні, такі трикутники подібні.

1) з обох боків і кутку між ними

Доведення:

Нехай у трикутників АВС і А 1 В 1 С 1 кут A дорівнює куту А 1 АВ дорівнює А 1 В 1 АС дорівнює А 1 С 1 . Доведемо, що трикутники рівні.

Накладемо трикутник ABC (або симетричний йому)на трикутник A 1 B 1 C 1 так, щоб кут A поєднався з кутом A 1 . Оскільки АВ=А 1 В 1 , а АС=А 1 З 1 , то B збігатиметься з В 1 , а C збігатиметься з С 1. Отже, трикутник А 1 В 1 С 1 збігається з трикутником АВС, а отже, дорівнює трикутнику АВС.

Теорему доведено.

2) збоку і прилеглих до неї кутів

Доведення:

Нехай АВС і А 1 В 1 С 1 - два трикутники, у яких АВ дорівнює А 1 В 1, кут А дорівнює куту А 1 і кут В дорівнює куту В 1 . Доведемо, що вони є рівними.

Накладемо трикутник ABC (або симетричний йому)на трикутник A 1 B 1 C 1 так, щоб AB співпало з A 1 B 1. Так як ∠ВАС = ∠В 1 А 1 С 1 і ∠АВС=∠А 1 В 1 С 1 , то промінь АС збігатиметься з А 1 З 1 , а ЗС збігається з В 1 З 1 . Звідси випливає, що вершина C збігатиметься з С 1. Отже, трикутник А 1 В 1 С 1 збігається з трикутником АВС, а отже, дорівнює трикутнику АВС.

Теорему доведено.

3) по трьох сторонах

Доведення :

Розглянемо трикутники ABC і A l B l C 1, у яких АВ = А 1 В 1 , BC = B l C 1 СА = С 1 А 1. Доведемо, що ΔАВС = ΔA 1 B 1 C 1 .

Докладемо трикутник ABC (або симетричний йому)до трикутника A 1 B 1 C 1 так, щоб вершина А поєдналася з вершиною A 1 , вершина В — з вершиною В 1 , а вершини С і С 1 виявилися по різні боки від прямої А 1 В 1 . Розглянемо 3 випадки:

1) Промінь З 1 З проходить всередині кута А 1 З 1 В 1 . Так як за умовою теореми сторони АС і A 1 C 1 , ВС і 1 С 1 рівні, то трикутники A 1 C 1 C і В 1 С 1 С - рівностегнові . За теоремою про властивість кутів рівнобедреного трикутника ∠1 = ∠2, ∠3 = ∠4, тому ∠ACB=∠A 1 C 1 B 1 .

2) Промінь З 1 З збігається з однією зі сторін цього кута. A лежить на CC1. AC=A 1 C 1 , BC=B 1 C 1 , C 1 BC - рівнобедрений , ∠ACB=∠A 1 C 1 B 1 .

3) Промінь C 1 C проходить поза кутом А 1 З 1 В 1 . AC=A 1 C 1 , BC=B 1 C 1 , отже, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1 .

Отже, AC=A 1 C 1 , BC=B 1 C 1 , ∠C=∠C 1 . Отже, трикутники ABC і A 1 B 1 C 1 дорівнюють
першою ознакою рівності трикутників.

Теорему доведено.

2. Розподіл відрізка на n рівних частин.

Провести промінь через A, відкласти у ньому n рівних відрізків. Через B та A n провести пряму і до неї паралельні через точки A 1 - A n -1. Зазначимо їх точки перетину з AB. Отримаємо n відрізків, які дорівнюють теоремі Фалеса.

Теорема Фалес. Якщо на одній із двох прямих відкласти послідовно кілька рівних відрізків і через їх кінці провести паралельні прямі, що перетинають другу пряму, то вони відсічуть на другій прямі рівні між собою відрізки.

Доведення. AB=CD

1. Проведемо через точки A та C прямі, паралельні іншій стороні кута. Отримаємо два паралелограми AB 2 B 1 A 1 і CD 2 D 1 C 1 . Відповідно до властивості паралелограма : AB 2 = A 1 B 1 і CD 2 = C 1 D 1 .

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 і рівні на підставі другої ознаки рівності трикутників:
AB = CD згідно з умовою теореми,
як відповідні, що утворилися при перетині паралельних BB 1 та DD 1 прямий BD.

3. Аналогічно кожен із кутів і виявляється рівним куту з вершиною в точці перетину січучих. AB 2 = CD 2 як відповідні елементи у рівних трикутниках.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Підгірний Максим

Матеріал дослідницької роботи може використовуватися для гуртків з геометрії у 7 класі

Завантажити:

Попередній перегляд:

МБУ ДО міста Ростова-на-Дону «Палац творчості дітей та молоді»

Донська академія наук молодих дослідників ім. Ю. А. Жданова

Математика

Тема: «Нестандартні теореми про рівність трикутників»

Підгірний Максим, 7 кл.

МБОУ ЗОШ № 3,

Керівник:

Олійникова Людмила Олександрівна,

вчитель математики,

МБОУ ЗОШ № 3,

м. Сальськ, Ростовська область

м. Ростов-на-Дону

2017 рік

Введение………………………………………………………….………………3

Основна частина

Ознаки рівності трикутників…………………………………………… 4

Нестандартні ознаки рівності трикутників………………………….7

Заключение…………………………………………………………………… 10

Список литературы…………………………………………………………… 11

додаток

Вступ.

Актуальність:

Трикутник одна з основних фігур у планіметрії. Я багато чув від старшокласників, що під час підготовки до ЄДІ їм часто доводиться доводити рівність трикутників. І виявляється недостатнім знання основних ознак. Мені захотілося дізнатися, чи можна довести рівність трикутників за іншими параметрами. У підручнику геометрії, яким навчаються учні нашої школи (автори Л.С.Атанасян, В.Ф.Бутузов та інших. Геометрія 7-9) розглядаються лише 3 ознаки рівності трикутників. Я переглянув учбово-методичні комплекти інших авторів. Але і в них для вивчення пропонуються лише три відомі теореми.

Гіпотеза:

Чи можливо сформулювати, крім трьох відомих, інші ознаки рівності трикутників?

Щоб переконатися, що відповідь на це питання хвилює не тільки мене, я провів соціологічне опитування серед учнів 7-11 класів див. додаток 1).

Мої припущення підтвердились. Більшість учнів знають лише три ознаки рівності трикутників.

Таким чином, метою мого дослідження стало віднайти нові ознаки рівності трикутників.

Завдання:

ΘВивчити літературу з досліджуваної теми.

ΘУточнити кількість ознак рівності трикутників.

ΘПродемонструвати своїм однокласникам та учням нашої школи існування інших ознак рівності трикутників та можливості їх доказу.

Об'єкт дослідження:

Вивчення ознак рівності трикутників.

Предмет дослідження. Трикутник як одна з основних фігур у планіметрії.

Метод дослідження:Теоретичний (вивчення, аналіз та синтез), системно-пошуковий, практичний (доказ теорем).

Історична довідка

Трикутник є одним із центральних фігур всієї геометрії.

При вирішенні завдань використовують його найрізноманітніші властивості.

Властивості трикутника широко застосовують практично: в архітектурі; при розробці креслення будівлі, плануванні майбутніх квартир; у промисловості, при проектуванні різних деталей, при виготовленні будматеріалів, при будівництві морських та авіа суден; у навігації для прокладання правильного та максимально точного маршруту; в астрології та астрономії трикутник є дуже значущою фігурою; трикутники роблять надійними конструкції високовольтних ліній електропередач та залізничних мостів.

Крім того, багато інших сфер, де застосовуються різні властивості трикутника: починаючи гру в більярд, необхідно розташувати кулі у вигляді трикутника, для цього використовують спеціальний пристрій; розстановка кеглів у грі Боулінг також у вигляді рівностороннього трикутника; для складання гарних паркетів використовують трикутники; пристрій трикутника Паскаля: кожне число дорівнює сумі двох розташованих над ним чисел (обвести трикутником три числа). Все просто, але скільки в цьому таїться чудес! Трикутник Паскаля комп'ютер переклав мовою кольору.

Тему трикутника можна продовжувати необмежено.

Яких лише трикутників немає на світі!

Існують також переносні значення цієї постаті: наприклад, правило «золотого трикутника» грунтується на психології покупця – знайшовши потрібний йому товар, покупець прямує до каси. Завдання продавців - змусити його затриматися в магазині довше, розташувавши потрібний покупцеві товар у вершинах уявного трикутника, тобто заякорити покупця. Чим більша площа трикутника, тим більш вдалим можна назвати планування магазину. У продуктовому магазині цими товарами-якорями є гастрономія, молочна продукція, хліб. Задня торцева стіна торгового залу є другим місцем за значимістю і саме там найдоцільніше розташовувати товари-якорі – саме для того, щоб змусити покупця пройти весь периметр магазину.

Широко відомий Бермудський трикутник - це район в Атлантичному океані, в якому нібито відбуваються таємничі зникнення морських і повітряних суден. Район обмежений лініями від Флориди до Бермудських островів, далі Пуерто-Ріко і назад до Флориди через Багами.

Тому вивчення трикутника та всіх його властивостей – дуже актуальна тема.

Мета цієї роботи – розповісти про ознаки рівності трикутників, що одна із найважливіших їх властивостей.

Ознаки рівності трикутників – це теореми, на підставі яких можна довести, що деякітрикутники рівні.

У геометрії використовують три ознаки рівності трикутників.

Ця тема практично вивчена, оскільки на сьогоднішній день існують три ознаки рівності трикутників, що доводяться за допомогою відповідних теорем.

У давнину разом з астрономією з'явилася наука – тригонометрія. Слово «тригонометрія» виготовлено від грецьких «трикутник» та «міряю». Буквальне значення - "наука про вимірювання трикутників".

За допомогою натягнутих мотузок завдовжки 3, 4 та 5 одиниць єгипетські жерці отримували прямі кути під час зведення храмів тощо.

Мистецтво зображати предмети на площині з Стародавніх часів привертає увагу людини, люди малювали на скелях, стінах, судинах та інших предметах побуту, різні орнаменти, рослини, тварин. Люди прагнули того, щоб зображення правильно відображало природну форму предмета.

Вчення про подобу фігур на основі теорії відносин і пропорцій було створено в Стародавній Греції в 5-4 століттях до н.е. і існує і розвивається досі. Наприклад, дуже багато дитячих іграшок подібним до предметів дорослого світу, взуття та одяг одного фасону випускається різних розмірів. Ці приклади можна продовжувати далі. Зрештою, всі люди подібні один до одного і як стверджує Біблія, створив їх бог за своїм образом і подобою.

Ознаки рівності трикутників мали здавна найважливіше значення геометрії, оскільки докази численних теорем зводилося до доказу рівності тих чи інших трикутників. Доказом ознак рівності трикутників займалися ще піфагорійці. За словами Прокла, Євдем Родоський приписує Фалесу Мілетському доказ про рівність двох трикутників, які мають рівними бік і два кути, що прилягають до неї (друга ознака рівності трикутників).

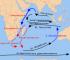
Цю теорему Фалес використовував визначення відстані від берега до морських кораблів.Яким чином користувався при цьому Фалес, достеменно не відомо.

Ознаки рівності трикутників.

Почнемо із визначення. Трикутники АВС та А1В1С1 називаються рівними, якщо їх можна поєднати накладенням.

Трикутник складається із шести елементів: трьох кутів і трьох сторін.

При цьому виникає питання: "Яку найменшу кількість елементів трикутника потрібно взяти для встановлення рівності двох трикутників?"

Ми не зможемо встановити рівність двох трикутників по одному елементу, тому що невідомо: "Чи будуть рівні інші елементи?"

Також неможливо встановити рівність двох трикутників, використовуючи два елементи через брак інформації встановлення рівності.

Можливе встановлення рівності двох трикутників, використовуючи три елементи. Але при цьому виникає питання: "Які саме три елементи потрібно назвати для встановлення рівності трикутників?"

При вивченні цього питання я переглянув шкільні підручники геометрії різних авторів, а також словники та довідники. У підручниках за сьомий клас запропоновано до вивчення лише три ознаки рівності трикутників.

Θ1 Ознака : Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні. рис.1

Доведення. Розглянемо трикутники ABC та A 1 B 1 C 1 , (рис. 1) у яких АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 . Доведемо, що ABC = A 1 B 1 C 1 .

Оскільки ∠А = ∠А 1 то трикутник ABC можна накласти на трикутник А 1 В 1 З 1 так, що вершина А поєднається з вершиною А 1 , а сторони АВ та АС накладуться відповідно на промені А 1 В 1 та A 1 C 1 . Оскільки АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ поєднається зі стороною А 1 В 1 а сторона АС – зі стороною А 1 C 1 ; зокрема, сумісні точки В і В 1 , С та C 1 . Отже, сумісні сторони ВС і В 1 З 1 . Отже, трикутники ABC та А 1 В 1 З 1 повністю поєднаються, отже, вони рівні.

А ось як у Стародавньому Єгипті застосували першу ознаку рівності трикутників. (по двох сторонах і кутку між ними), творцем його також вважається Фалес Мілетський, для вимірювання висоти піраміди: уявімо, що ми стоїмо перед величезною пірамідою, як виміряти її висоту? Адже до неї не додаси вимірювальних приладів! І тут на допомогу Фалесу Мілетському приходить перша ознака рівності трикутників: він почекав поки тінь його точно збігається з його зростанням, застосував теорему, вийшло, що висота піраміди дорівнює її тіні (рис. 2).

Мал. 2

Θ2 Ознака: Якщо сторона і два прилеглих до неї кута одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.

Доказ: Якщо у ΔАВС та ΔА 1 В 1 З 1 матимуть місце такі рівності AB=А 1 В 1 , ∠BAC=∠B 1 A 1 C 1 , ∠АВС= ∠А 1 В 1 С 1 . Накладемо один на одного трикутники А 1 В 1 З 1 і АВС таким чином, щоб збіглися рівні сторони AB та А 1 В 1 та кути, які до них прилягають. Як і в попередньому прикладі, якщо це необхідно, трикутник А 1 В 1 З 1 можна "перевернути та прикласти зворотною стороною". Трикутники співпадуть, отже вони можуть вважатися рівними.

Θ3 Ознака : Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні. Доказ: Нехай для ABC і A 1 B 1 C 1 справедливі рівності А 1 В 1 =АВ, В 1 С 1 =ВС, С 1 А 1 =СА. Перемістимо трикутник А 1 В 1 З 1 таким чином, що сторона А 1 В 1 збігається зі стороною АВ, і вершини B 1 та B, A 1 та A, збігатимуться. Візьмемо коло з центром A і радіусом AC, і друге коло з центром B і радіусом BC. Ці кола перетнуться у двох симетричних щодо відрізка AB точках: точкою C та точкою C 2 . Отже, C1 після перенесення трикутника A1B1C1 має збігатися або з точками C або з C2. У будь-якому випадку це означатиме рівність ΔABC=ΔA 1 B 1 C 1 , так як трикутники ABC = ABC 2 рівні (адже трикутники є симетричними щодо відрізка AB .

Ця властивість – жорсткість трикутника – широко використовується практично. Так, щоб закріпити стовп у вертикальному положенні, до нього ставлять підпір; такий самий принцип використовується при встановленні кронштейна.

Властивість жорсткості трикутника широко використовують у практиці під час будівництва залізних конструкцій.

З третьої ознаки рівності трикутників випливає, що трикутник – жорстка постать. Тому що: можна уявити собі дві рейки, у яких два кінці скріплені цвяхом. Така конструкція не є жорсткою, проте, зсуваючи або розсуваючи вільні кінці рейок, ми можемо змінювати кут між ними. Тепер візьмемо ще одну рейку і скріпимо її кінці з вільними кінцями перших двох рейок. Отримана конструкція – трикутник – буде вже жорсткою. У ній не можна зрушити або розсунути жодні дві сторони, тобто не можна змінити жоден кут. Справді, якби це вдалося, ми отримали б новий трикутник, не рівний вихідному. Але це неможливо, тому що новий трикутник повинен дорівнювати вихідному по третьому

У довіднику з елементарної математики М. Я. Вигодського знайшов ще одна ознака.

Θ4 Ознака: Якщо дві сторони та кут, що лежить проти більшої з них одного трикутника відповідно дорівнюють двом сторонам і куту, що лежить проти більшої з них іншого трикутника, то такі трикутники рівні.

Доведу цю ознаку.

Дано : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1,∠ B= ∠ B1

Довести: ABC=A1B1C1.

Розташуємо трикутники так, як на малюнку 1 . З'єднаємо B і B1, тоді ΔАВВ1

Рівнобедрений, значить∠ 1= ∠ 2. ∠ 3= ∠ 4 як залишки рівних кутів.

Отримаємо ΔВСВ1- рівнобедрений, звідси ВС = В1С1. ΔАВС = ΔА1В1С1 по трьох сторонах.

Також у шкільному курсі розглядаються 4 ознаки рівності прямокутних трикутників:

Θ1 . Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні.

Θ2 . Якщо катет і гострий кут одного прямокутного трикутника, що прилягає до нього, відповідно дорівнюють катету і прилеглому до нього гострому куту іншого, то такі трикутники рівні.

Θ3 . Якщо гіпотенуза та гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту іншого, то такі трикутники рівні.

Θ4 . Якщо гіпотенуза і катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі та катету іншого, то такі трикутники рівні.

Я вирішив теоретичну базу за ознаками рівності трикутників, додавши до сторін і кутів, що використовуються в класичних ознаках рівності трикутників, інші компоненти: бісектрису, медіану та висоту.

Нестандартні ознаки рівності трикутників.

1) По обидва боки та висоту проведеної до однієї з них.

Дано: AB=A1B1, BC=B1C1, AK=A1K1,

Довести: ABC = A1B1C1 .

Доказ: ΔABK=ΔA1B1K1 з гіпотенузи та катету, тоді∠ B= ∠ B1 і отримаємо ABC = A1B1C1 за першою ознакою.

2) З обох сторін та медіані, проведеної до однієї з них

Дано: AB=A1B1, BC=B1C1, AK=A1K1, AK та A1K1 - медіани.

Довести: ABC = A1B1C1 .

Доказ: ΔABK = ΔA1B1K1 по трьох сторонах, значить∠ B= ∠ B1 і ABC = A1B1C1 за першою ознакою.

3) По обидва боки і висоту, проведеної з третього кута.

Дано: ∠ B = ∠ B1 , ∠ C = ∠ C1 , AK = A1K1 .

Довести: ABC = A1B1C1 .

Доказ: ΔABK=ΔA1B1K1 по катету та гострому куту, означає BK=B1K1 ,

ΔACK=ΔA1C1K1 за катетом і гострим кутом, означає KC=K1C1 , а отже BC=B1C1 , а ΔABC= ΔA1B1C1 за другою ознакою.

4) По стороні та двом висотам, проведеним з кутів, прилеглих до цієї сторони.

Дано: АС = А1С1, СМ = С1М1, АК = А1К1.

Довести: ΔСC= ΔA1B1C1 .

Доказ: ΔAМC= ΔA1М1C1 по катету та гіпотенузі, значить∠ А = ∠ А1 , а ΔAКC= ΔA1К1C1 по катету та гіпотенузі, значить∠ С = ∠ С1 .

Отже, ABC = A1B1C1 за другою ознакою.

5) По двох сторонах і висоті, проведеної до третьої сторони.

Дано: АВ = А1В1, ВС = В1С1, ВК = В1К1.

Довести: ABC = A1B1C1 .

Доведення: ΔABK=ΔA1B1K1 з гіпотенузи та катету, означає AK=A1K1,

ΔBКC= ΔB1К1C1 по катету та гіпотенузі, значить KC=K1C1 .

Отже, ABC = A1B1C1 по трьох сторонах.

6) По стороні, одному з кутів, що прилягають до цієї сторони та бісектрисі з цього кута.

Дано: АС = А1С1, АК = А1К1,∠ А ∠ А1.

Довести: ABC = A1B1C1 .

Доказ: ΔКАС=ΔК1А1С1 за першою ознакою, отже∠ С = ∠ С1 ,

ΔABC= ΔA1B1C1 за другою ознакою.

7) За двома висотами і кутом, з якого проведена одна з висот.

Дано: СМ = С1М1, АК = А1К1, ∠ А ∠ А1 .

Довести: ABC = A1B1C1 .

Доказ: ΔAМC= ΔA1М1C1 за катетом та гострим кутом,ΔКАС=ΔК1А1С1 по катету та гіпотенузі, ΔABC= ΔA1B1C1 за другою ознакою.

Висновок.

У ході дослідження я з'ясував, що крім трьох основних ознак рівності трикутників можна вказати чимало інших. Я сформулював і довів рівність трикутників за медіаною, висотою, бісектрисою трикутника у поєднанні зі сторонами та кутами трикутника, дотримуючись наявності трьох елементів. Тепер я можу розповісти учням нашої школи, що є інші ознаки рівності трикутників. Це дозволить випускникам школи застосувати результати моїх досліджень під час підготовки до ОДЕ та ЄДІ та легко вирішувати геометричні завдання на застосування цих ознак.

Результат мого дослідження: Доведено кілька ознак рівності трикутників, які не вивчаються у шкільному курсі геометрії.

Список літератури

Вигодський М.Я. Довідник з елементарної математики.
Геометрія. 7-9 класи: навч. Для загальноосвіт. установ/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев та ін. – 19-те вид. - М.: Просвітництво, 2009.
Погорєлов А. В. Геометрія: Навч. Для 7-9 кл. загальноосвіт. Установ. – 3-тє видання. - М.: Просвітництво, 2002.
. Енциклопедія «Аванта» з математики, Москва, 2004
2. «Вікіпедія» – вільна енциклопедія.
3. Глейзер Г.І. «Історія математики у шкільництві», Москва, Просвітництво, 1982 р.
4. Гусєва Т.М. Ознаки подоби трикутників.- Москва, Перше вересня, додаток «Математика», 1999, №28
5. Погорєлов А.В. «Геометрія 7-9 класи»,Москва, Просвітництво, 2003

Додаток 1

1.Як ви вважаєте, скільки існує ознак рівності трикутників?

А) 3 Б) більше трьох В) менше трьох

2. Чи хотіли б ви дізнатися про нові ознаки рівності трикутників?

А) так Б) ні

Два трикутники називаються рівними, якщо їх можна поєднати накладенням. На малюнку 1 зображені рівні трикутники ABC і А1В1С1. Кожен із цих трикутників можна накласти на інший так, що вони повністю суміщаться, тобто попарно поєднаються їхні вершини та сторони. Ясно, що при цьому попарно поєднаються і кути цих трикутників.

Таким чином, якщо два трикутники рівні, то елементи (тобто сторони та кути) одного трикутника відповідно дорівнюють елементам іншого трикутника. Відмітимо, що у рівних трикутниках проти відповідно рівних сторін(тобто поєднуються при накладенні) лежать рівні кути,і назад: проти відповідно рівних кутів лежать рівні боки.

Так, наприклад, у рівних трикутниках ABC і A 1 B 1 C 1 , зображених на малюнку 1, проти відповідно рівних сторін АВ і А 1 В 1 лежать рівні кути З і С 1 . Рівність трикутників ABC і А1В1С1 позначатимемо так: ΔABC = ΔА1В1С1. Виявляється, що рівність двох трикутників можна встановити, порівнюючи деякі їх елементи.

Теорема 1. Перша ознака рівності трикутників.Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні (рис.2).

Доведення. Розглянемо трикутники ABC і A 1 B 1 C 1 , які мають АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 (див. рис.2). Доведемо, що ABC = A 1 B 1 C 1 .

Так як ∠ А = ∠ А 1 , то трикутник ABC можна накласти на трикутник А 1 В 1 С 1 так, що вершина А суміситься з вершиною А 1 , а сторони АВ та АС накладуться відповідно на промені А 1 В 1 та A 1 C 1 . Оскільки АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ поєднається зі стороною А 1 В 1 а сторона АС - зі стороною А 1 C 1 ; зокрема, суміщаються точки В і В 1 , З і C 1 . Отже, суміщаються сторони ЗС і В1С1. Отже, трикутники ABC та А 1 В 1 С 1 повністю суміщаються, отже, вони рівні.

Аналогічно шляхом накладання доводиться теорема 2.

Теорема 2. Друга ознака рівності трикутників.Якщо сторона і два кути одного трикутника, що до неї прилягають, відповідно рівні стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні (рис. 34).

Зауваження. На основі теореми 2 встановлюється теорема 3.

Теорема 3. Сума будь-яких двох внутрішніх кутів трикутника менша за 180°.

З останньої теореми випливає теорема 4.

Теорема 4. Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний з ним.

Теорема 5. Третя ознака рівності трикутників.Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні ().

приклад 1.У трикутниках ABC та DEF (рис. 4)

∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Порівняти трикутники ABC та DEF. Який кут у трикутнику DEF дорівнює куту?

Рішення. Дані трикутники дорівнюють за першою ознакою. Кут F трикутника DEF дорівнює куту трикутника ABC, так як ці кути лежать проти відповідно рівних сторін DE і АС.

приклад 2.Відрізки АВ та CD (рис. 5) перетинаються у точці О, яка є серединою кожного з них. Чому дорівнює відрізок BD, якщо відрізок АС дорівнює 6 м?

Рішення. Трикутники АОС та BOD рівні (за першою ознакою): ∠ АОС = ∠ BOD (вертикальні), АВ = ОВ, СО = OD (за умовою).
З рівності цих трикутників випливає рівність їх сторін, тобто АС = BD. Але оскільки за умовою АС = 6 м, то BD = 6 м.