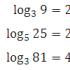Примери с логаритми и тяхното решение на изпита. Решаване на логаритмични уравнения

Какво е логаритъм?

Внимание!
Има допълнителни
материал в специален раздел 555.
За тези, които силно "не много..."
И за тези, които "много...")

Какво е логаритъм? Как се решават логаритми? Тези въпроси объркват много завършили. Традиционно темата за логаритмите се счита за сложна, неразбираема и страшна. Особено - уравнения с логаритми.

Това абсолютно не е вярно. Абсолютно! Не вярвате? Добре. Сега, за около 10 - 20 минути вие:

1. Разберете какво е логаритъм.

2. Научете се да решавате цял клас експоненциални уравнения. Дори и да не сте чували за тях.

3. Научете се да изчислявате прости логаритми.

Освен това, за това ще трябва само да знаете таблицата за умножение и как числото се повишава до степен ...

Чувствам, че се съмняваш... Е, имай време! Отивам!

Първо, решете следното уравнение наум:

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаването на примери и да разберете нивото си. Тестване с незабавна проверка. Учене - с интерес!)

можете да се запознаете с функции и производни.

Вашата поверителност е важна за нас. Поради тази причина разработихме Политика за поверителност, която описва как използваме и съхраняваме вашата информация. Моля, прочетете нашата политика за поверителност и ни уведомете, ако имате въпроси.

Събиране и използване на лична информация

Личната информация се отнася до данни, които могат да бъдат използвани за идентифициране или връзка с конкретно лице.

Може да бъдете помолени да предоставите личната си информация по всяко време, когато се свържете с нас.

Следват някои примери за видовете лична информация, която можем да събираме и как можем да използваме такава информация.

Каква лична информация събираме:

• Когато подадете заявление на сайта, ние може да събираме различна информация, включително вашето име, телефонен номер, имейл адрес и т.н.

Как използваме вашата лична информация:

• Личната информация, която събираме, ни позволява да се свържем с вас и да ви информираме за уникални оферти, промоции и други събития и предстоящи събития.
• От време на време може да използваме вашата лична информация, за да ви изпращаме важни известия и съобщения.
• Можем също така да използваме лична информация за вътрешни цели, като извършване на одити, анализ на данни и различни изследвания, за да подобрим услугите, които предоставяме, и да ви предоставим препоръки относно нашите услуги.
• Ако участвате в теглене на награди, конкурс или подобен стимул, ние може да използваме предоставената от вас информация, за да администрираме такива програми.

Разкриване на трети страни

Ние не разкриваме получената от вас информация на трети страни.

Изключения:

• В случай, че е необходимо - в съответствие със закона, съдебния ред, в съдебно производство и/или въз основа на публични искания или искания от държавни органи на територията на Руската федерация - разкрийте личната си информация. Може също да разкрием информация за вас, ако преценим, че такова разкриване е необходимо или подходящо за сигурност, правоприлагане или други причини от обществен интерес.
• В случай на реорганизация, сливане или продажба, ние можем да прехвърлим личната информация, която събираме, на съответния правоприемник на трета страна.

Защита на личната информация

Ние вземаме предпазни мерки – включително административни, технически и физически – за да защитим вашата лична информация от загуба, кражба и злоупотреба, както и от неоторизиран достъп, разкриване, промяна и унищожаване.

Поддържане на вашата поверителност на ниво компания

За да гарантираме, че вашата лична информация е защитена, ние съобщаваме практиките за поверителност и сигурност на нашите служители и стриктно прилагаме практиките за поверителност.

Логаритмични изрази, решение на примери. В тази статия ще разгледаме проблеми, свързани с решаването на логаритми. Задачите поставят въпроса за намиране на стойността на израза. Трябва да се отбележи, че понятието логаритъм се използва в много задачи и е изключително важно да се разбере значението му. Що се отнася до USE, логаритъмът се използва при решаване на уравнения, в приложни задачи, а също и в задачи, свързани с изучаване на функции.

Ето примери, за да разберете самото значение на логаритъма:

Основна логаритмична идентичност:

Свойства на логаритмите, които винаги трябва да помните:

*Логаритъмът на произведението е равен на сбора от логаритмите на факторите.

* * *

* Логаритъмът на частното (дроба) е равен на разликата от логаритмите на факторите.

* * *

* Логаритъмът на степента е равен на произведението на степента и логаритъма на нейната основа.

* * *

*Преход към нова база

* * *

Още имоти:

* * *

Изчисляването на логаритми е тясно свързано с използването на свойствата на степените.

Ние изброяваме някои от тях:

Същността на това свойство е, че при прехвърляне на числителя към знаменателя и обратно, знакът на степента се променя на противоположния. Например:

Последица от това свойство:

* * *

При повишаване на степен в степен, основата остава същата, но степените се умножават.

* * *

Както можете да видите, самата концепция на логаритъма е проста. Основното е, че е необходима добра практика, която дава определено умение. Разбира се познаването на формулите е задължително. Ако умението за преобразуване на елементарни логаритми не се формира, тогава при решаване на прости задачи човек може лесно да направи грешка.

Упражнявайте се, решавайте първо най-простите примери от курса по математика, след това преминете към по-сложни. В бъдеще определено ще покажа как се решават „грозните“ логаритми, няма да има такива на изпита, но представляват интерес, не го пропускайте!

Това е всичко! Късмет!

С уважение, Александър Крутицки

P.S: Ще бъда благодарен, ако разкажете за сайта в социалните мрежи.

В този видео урок ще разгледаме решаването на доста сериозно логаритмично уравнение, в което не само трябва да намерите корените, но и да изберете тези, които лежат на даден сегмент.

Задача C1. Решете уравнението. Намерете всички корени на това уравнение, които принадлежат на интервала.

Бележка за логаритмичните уравнения

Въпреки това от година на година при мен идват студенти, които се опитват да решат такива, честно казано, трудни уравнения, но в същото време не могат да разберат: откъде изобщо започват и как да подходят към логаритмите? Такъв проблем може да възникне дори при силни, добре подготвени ученици.

В резултат на това мнозина започват да се страхуват от тази тема или дори се смятат за глупави. Така че, запомнете: ако не можете да решите такова уравнение, това изобщо не означава, че сте глупави. Защото, например, можете да се справите с това уравнение почти устно:

log 2 x = 4

И ако това не е така, нямаше да четете този текст сега, защото бяхте заети с по-прости и обикновени задачи. Разбира се, сега някой ще възрази: „Какво общо има това най-просто уравнение с нашия здравословен дизайн?“ Отговарям: всяко логаритмично уравнение, колкото и сложно да е то, в крайна сметка се свежда до толкова прости, вербално решени конструкции.

Разбира се, необходимо е да се премине от сложни логаритмични уравнения към по-прости не с помощта на избор или танци с тамбурин, а според ясни, отдавна дефинирани правила, които се наричат ​​така - правила за преобразуване на логаритмични изрази. Познавайки ги, можете лесно да разберете дори и най-сложните уравнения на изпита по математика.

И именно за тези правила ще говорим в днешния урок. Отивам!

Решаване на логаритмичното уравнение в задача C1

Така че нека решим уравнението:

На първо място, когато става дума за логаритмични уравнения, припомняме основната тактика - ако мога да кажа, основното правило за решаване на логаритмични уравнения. Състои се в следното:

Теорема за каноничната форма. Всяко логаритмично уравнение, независимо какво включва, без значение какви логаритми, без значение каква е основата и без значение какво c има в себе си, е необходимо да го доведем до уравнение от вида:

log a f (x ) = log a g (x )

Ако погледнем нашето уравнение, веднага забелязваме два проблема:

1. Отляво имаме сумата от две числа, единият от които изобщо не е логаритъм.
2. Вдясно е доста логаритъм, но в основата му е корен. А логаритъмът отляво има само 2, т.е. основите на логаритмите отляво и отдясно са различни.

Така че излязохме със списък с проблеми, които отделят нашето уравнение от това канонично уравнение, към което трябва да намалите всяко логаритмично уравнение в процеса на решаване. По този начин решаването на нашето уравнение на този етап се свежда до елиминиране на двата проблема, описани по-горе.

Всяко логаритмично уравнение може да бъде решено бързо и лесно, ако се сведе до неговата канонична форма.

Сборът от логаритмите и логаритъма на произведението

Да продължим по ред. Първо, нека се справим със структурата, която стои отляво. Какво можем да кажем за сбора от два логаритма? Нека си спомним прекрасната формула:

log a f (x) + log a g (x) = log a f (x) g (x)

Но си струва да се има предвид, че в нашия случай първият член изобщо не е логаритъм. Така че, трябва да представите единицата като логаритъм на база 2 (а именно 2, защото логаритъмът на база 2 е отляво). Как да го направим? Отново запомнете прекрасната формула:

a = log b b a

Тук трябва да разберете: когато казваме „Всяка основа b“, тогава имаме предвид, че b все още не може да бъде произволно число. Ако вмъкнем число в логаритъма, върху него веднага се наслагват определени числа. ограничения, а именно: основата на логаритъма трябва да е по-голяма от 0 и не трябва да е равна на 1. В противен случай логаритъмът просто няма смисъл. Нека го запишем:

0 < b ≠ 1

Нека видим какво се случва в нашия случай:

1 = log 2 2 1 = log 2 2

Сега нека пренапишем цялото си уравнение, като имаме предвид този факт. И веднага прилагаме друго правило: сумата от логаритмите е равна на логаритъма на произведението на аргументите. В резултат на това получаваме:

Имаме ново уравнение. Както виждате, това вече е много по-близо до каноничното изравняване, към което се стремим. Но има един проблем, написахме го под формата на втората точка: нашите логаритми, които са отляво и отдясно, различни основания. Нека да преминем към следващата стъпка.

Правила за вземане на степени от логаритъма

Така че логаритъмът отляво има основа само 2, а логаритъмът отдясно има корен в основата. Но и това не е проблем, ако си спомним, че от основите от аргументите на логаритъма може да се изведе на степен. Нека напишем едно от тези правила:

log a b n = n log a b

Превод на човешки език: можете да извадите степента от основата на логаритъма и да я поставите отпред като фактор. Числото n "мигрира" от логаритъма и се превърна в коефициент отпред.

Можем и да извадим силата от основата на логаритъма. Ще изглежда така:

С други думи, ако извадите степента от аргумента логаритъм, тази степен също се записва като множител пред логаритъма, но не като число, а като реципрочна стойност на 1/k.

Това обаче не е всичко! Можем да комбинираме тези две формули и да излезем със следната формула:

Когато експонентът е както в основата, така и в аргумента на логаритъм, можем да спестим време и да опростим изчисленията, като премахнем експонентите и от основата, и от аргумента наведнъж. В този случай това, което е било в аргумента (в нашия случай това е коефициентът n), ще бъде в числителя. И каква е била степента в основата, a k , ще отиде в знаменателя.

И точно тези формули ще използваме сега, за да сведем логаритмите си до една и съща основа.

На първо място, ще изберем повече или по-малко красива основа. Очевидно двойката в основата е много по-приятна за работа, отколкото с корена. Така че нека се опитаме да базираме втория логаритъм на 2. Нека напишем този логаритъм отделно:

Какво можем да направим тук? Припомнете си формулата за степен с рационален показател. С други думи, можем да запишем корени като степен с рационален показател. И тогава изваждаме степента на 1/2 както от аргумента, така и от основата на логаритъма. Намаляваме двойките в коефициентите в числителя и знаменателя пред логаритъма:

Накрая пренаписваме оригиналното уравнение, като вземем предвид новите коефициенти:

log 2 2 (9x 2 + 5) = log 2 (8x 4 + 14)

Получихме каноничното логаритмично уравнение. И отляво, и отдясно имаме логаритъм в една и съща основа 2. Освен тези логаритми няма коефициенти, няма членове нито отляво, нито отдясно.

Следователно можем да се отървем от знака на логаритъма. Разбира се, като се вземе предвид областта на дефиниция. Но преди да направим това, нека се върнем назад и да направим малко пояснение относно дробите.

Разделяне на дроб на дроб: допълнителни съображения

Не всички ученици разбират откъде идват и къде отиват факторите пред правилния логаритъм. Нека го запишем отново:

Нека разберем какво е дроб. Нека напишем:

И сега си припомняме правилото за разделяне на дроби: за да разделите на 1/2, трябва да умножите по обърнатата дроб:

Разбира се, за удобство на по-нататъшните изчисления, можем да запишем двойката като 2/1 - и точно това наблюдаваме като втори коефициент в процеса на решаване.

Надявам се сега всички да разберат откъде идва вторият коефициент, така че да преминем директно към решаването на нашето канонично логаритмично уравнение.

Да се ​​отървем от знака на логаритъма

Напомням ви, че сега можем да се отървем от логаритмите и да оставим следния израз:

2(9x2 + 5) = 8x4 + 14

Нека разширим скобите вляво. Получаваме:

18x2 + 10 = 8x4 + 14

Нека преместим всичко от лявата страна на дясната:

8x4 + 14 - 18x2 - 10 = 0

Ние даваме подобни и получаваме:

8x4 - 18x2 + 4 = 0

Можем да разделим двете страни на това уравнение на 2, за да опростим коефициентите, и получаваме:

4x4 - 9x2 + 2 = 0

Пред нас е обичайното биквадратно уравнение, а корените му лесно се изчисляват по отношение на дискриминанта. Така че нека напишем дискриминанта:

D = 81 - 4 4 2 \u003d 81 - 32 = 49

Добре, Discriminant е "красив", коренът му е 7. Това е всичко, ние считаме самите X. Но в този случай корените ще се окажат не x, а x 2, защото имаме биквадратично уравнение. Така че нашите опции са:

Моля, обърнете внимание: извадихме корените, така че ще има два отговора, т.к. квадрат - равномерна функция. И ако напишем само корен от две, тогава просто ще загубим втория корен.

Сега рисуваме втория корен на нашето биквадратно уравнение:

Отново вземаме аритметичния квадратен корен от двете страни на нашето уравнение и получаваме два корена. Запомнете обаче:

Не е достатъчно просто да се приравнят аргументите на логаритмите в канонична форма. Запомнете обхвата!

Общо получихме четири корена. Всички те наистина са решения на нашето оригинално уравнение. Погледнете: в нашето оригинално логаритмично уравнение, вътре в логаритмите е или 9x 2 + 5 (тази функция винаги е положителна), или 8x 4 + 14 - тя също винаги е положителна. Следователно областта на дефиниция на логаритмите е изпълнена във всеки случай, без значение какъв корен получаваме, което означава, че и четирите корена са решения на нашето уравнение.

Чудесно, сега да преминем към втората част на проблема.

Избор на корени на логаритмично уравнение върху сегмент

Избираме от нашите четири корена тези, които лежат на интервала [−1; 8/9]. Връщаме се към нашите корени и сега ще извършим тяхната селекция. За начало предлагам да начертаете координатна ос и да маркирате краищата на сегмента върху нея:

И двете точки ще бъдат засенчени. Тези. според условието на задачата се интересуваме от защрихования сегмент. Сега нека се заемем с корените.

Ирационални корени

Нека започнем с ирационалните корени. Имайте предвид, че 8/9< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

От това следва, че коренът от две не попада в интересуващия ни сегмент. По същия начин получаваме с отрицателен корен: той е по-малък от −1, т.е. лежи вляво от сегмента, който ни интересува.

рационални корени

Остават два корена: x = 1/2 и x = −1/2. Нека забележим, че левият край на сегмента (−1) е отрицателен, а десният край (8/9) е положителен. Следователно някъде между тези краища се намира числото 0. Коренът x = −1/2 ще бъде между −1 и 0, т.е. ще бъдат включени в крайния отговор. Правим същото с корена x = 1/2. Този корен също лежи върху разглеждания сегмент.

Много е лесно да се уверите, че числото 8/9 е по-голямо от 1/2. Нека извадим тези числа едно от друго:

Получаваме дроб 7/18 > 0, което по дефиниция означава, че 8/9 > 1/2.

Нека маркираме подходящи корени по координатната ос:

Крайният отговор ще бъде два корена: 1/2 и −1/2.

Сравнение на ирационални числа: универсален алгоритъм

В заключение бих искал да се върна отново към ирационалните числа. Използвайки техния пример, сега ще видим как да сравняваме рационални и ирационални величини в математиката. Като начало между тях има такава отметка V - знакът "повече" или "по-малко", но все още не знаем в коя посока е насочен. Нека напишем:

Защо изобщо се нуждаем от алгоритми за сравнение? Факт е, че в този проблем имахме голям късмет: в процеса на решаване възникна разделящо число 1, за което определено можем да кажем:

Въпреки това, не винаги ще видите такъв номер в движение. Затова нека се опитаме да сравним нашите числа директно, директно.

Как се прави? Правим същото като с обичайните неравенства:

1. Първо, ако някъде имахме отрицателни коефициенти, тогава щяхме да умножим двете страни на неравенството по −1. Разбира се смяна на знака. Такава отметка V би се променила в такава - Λ.
2. Но в нашия случай и двете страни вече са положителни, така че няма нужда да променяте нищо. Това, което наистина е необходимо е квадрат и двете странида се отървем от радикала.

Ако при сравняване на ирационални числа не е възможно да се вземе разделителен елемент в движение, препоръчвам да извършите такова сравнение "на челото" - описвайки го като обикновено неравенство.

При решаването му изглежда така:

Сега всичко е лесно за сравнение. Факт е, че 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

Това е всичко, получихме строго доказателство, че всички числа са отбелязани на числовата права x правилно и точно в последователността, в която всъщност трябва да бъдат. Никой няма да се оплаче от такова решение, така че запомнете: ако не видите веднага разделящото число (в нашия случай това е 1), тогава не се колебайте да напишете горната конструкция, умножете, квадратирайте - и накрая вие ще получи красиво неравенство. От това неравенство ще стане ясно кое точно число е по-голямо и кое по-малко.

Връщайки се към нашия проблем, бих искал още веднъж да насоча вниманието ви към това, което направихме в самото начало при решаването на нашето уравнение. А именно, ние разгледахме отблизо нашето оригинално логаритмично уравнение и се опитахме да го сведем до канониченлогаритмично уравнение. Където има само логаритми отляво и отдясно - без допълнителни членове, коефициенти отпред и т.н. Не са ни необходими два логаритъма към основата a или b, а именно логаритъм равен на друг логаритъм.

Освен това основите на логаритмите също трябва да са равни. В същото време, ако уравнението е съставено правилно, тогава с помощта на елементарни логаритмични трансформации (сумата от логаритми, преобразуване на число в логаритъм и т.н.), ще сведем това уравнение до каноничното.

Следователно, отсега нататък, когато видите логаритмично уравнение, което не е решено веднага „на челото“, не трябва да се губите или да се опитвате да намерите отговор. Достатъчно е да следвате тези стъпки:

1. Приведете всички свободни елементи към логаритъма;
2. След това добавете тези логаритми;
3. В получената конструкция всички логаритми водят до една и съща основа.

В резултат на това ще получите просто уравнение, което може да бъде решено с елементарни средства на алгебрата от материали от 8-9 клас. Като цяло, отидете на моя сайт, практикувайте решаване на логаритми, решавайте логаритмични уравнения като мен, решавайте ги по-добре от мен. И това е всичко за мен. Павел Бердов беше с вас. Ще се видим скоро!

Както знаете, когато умножавате изрази със степени, техните експоненти винаги се сумират (a b * a c = a b + c). Този математически закон е изведен от Архимед, а по-късно, през 8-ми век, математикът Вирасен създава таблица с целочислени показатели. Именно те послужиха за по-нататъшното откриване на логаритмите. Примери за използване на тази функция могат да бъдат намерени почти навсякъде, където е необходимо да се опрости тромавото умножение до просто събиране. Ако отделите 10 минути, четейки тази статия, ще ви обясним какво представляват логаритмите и как да работите с тях. Прост и достъпен език.

Определение в математиката

Логаритъмът е израз в следната форма: log ab=c, тоест логаритъмът на всяко неотрицателно число (тоест всяко положително) "b" по неговата основа "a" се счита за степента на "c" , до което трябва да се повдигне основата "a", така че накрая да се получи стойността "b". Нека анализираме логаритъма с помощта на примери, да кажем, че има израз log 2 8. Как да намерим отговора? Много е просто, трябва да намерите такава степен, че от 2 до необходимата степен да получите 8. След като направихме някои изчисления в ума си, получаваме числото 3! И правилно, защото 2 на степен 3 дава числото 8 в отговора.

Разновидности на логаритмите

За много ученици и студенти тази тема изглежда сложна и неразбираема, но всъщност логаритмите не са толкова страшни, основното е да разберете общото им значение и да запомните техните свойства и някои правила. Има три различни вида логаритмични изрази:

1. Естествен логаритъм ln a, където основата е числото на Ойлер (e = 2.7).
2. Десетична а, където основата е 10.
3. Логаритъмът на произволно число b спрямо основата a>1.

Всеки от тях се решава по стандартен начин, включващ опростяване, редукция и последващо свеждане до един логаритъм с помощта на логаритмични теореми. За да получите правилните стойности на логаритмите, трябва да запомните техните свойства и реда на действията в техните решения.

Правила и някои ограничения

В математиката има няколко правила-ограничения, които се приемат като аксиома, тоест не подлежат на обсъждане и са верни. Например, не е възможно числата да се разделят на нула, а също така е невъзможно да се извлече корен от четна степен от отрицателни числа. Логаритмите също имат свои собствени правила, следвайки които лесно можете да научите как да работите дори с дълги и обемни логаритмични изрази:

• основата "a" винаги трябва да е по-голяма от нула и в същото време да не е равна на 1, в противен случай изразът ще загуби смисъла си, тъй като "1" и "0" до всяка степен винаги са равни на техните стойности;
• ако a > 0, тогава a b > 0, се оказва, че "c" трябва да е по-голямо от нула.

Как се решават логаритми?

Например, като се има предвид задачата да се намери отговорът на уравнението 10 x \u003d 100. Много е лесно, трябва да изберете такава степен, като повишите числото десет, до което получаваме 100. Това, разбира се, е 10 2 \u003d 100.

Сега нека представим този израз като логаритмичен. Получаваме log 10 100 = 2. При решаване на логаритми всички действия на практика се сближават с намирането на степента, до която трябва да се въведе основата на логаритъма, за да се получи дадено число.

За да определите точно стойността на неизвестна степен, трябва да научите как да работите с таблица с градуси. Изглежда така:

Както можете да видите, някои експоненти могат да бъдат отгатнати интуитивно, ако имате технически начин на мислене и познания за таблицата за умножение. Въпреки това, по-големи стойности ще изискват таблица за мощност. Може да се използва дори от тези, които не разбират нищо от сложни математически теми. Лявата колона съдържа числа (база а), горният ред числа е стойността на степента c, до която се повдига числото a. На пресечната точка в клетките се определят стойностите на числата, които са отговорът (a c = b). Нека вземем например първата клетка с числото 10 и я квадратираме, получаваме стойността 100, която е посочена в пресечната точка на нашите две клетки. Всичко е толкова просто и лесно, че дори най-истинският хуманист ще разбере!

Уравнения и неравенства

Оказва се, че при определени условия степента е логаритъмът. Следователно всякакви математически числови изрази могат да бъдат записани като логаритмично уравнение. Например, 3 4 = 81 може да се запише като логаритъм от 81 към основа 3, което е четири (log 3 81 = 4). За отрицателните степени правилата са едни и същи: 2 -5 = 1/32 записваме като логаритъм, получаваме log 2 (1/32) = -5. Един от най-увлекателните раздели на математиката е темата за "логаритмите". Ще разгледаме примери и решения на уравнения малко по-ниско, веднага след изучаване на техните свойства. Сега нека разгледаме как изглеждат неравенствата и как да ги разграничим от уравненията.

Даден е израз от следния вид: log 2 (x-1) > 3 - това е логаритмично неравенство, тъй като неизвестната стойност "x" е под знака на логаритъма. И също така в израза се сравняват две количества: логаритъмът на желаното число в основа две е по-голям от числото три.

Най-важната разлика между логаритмичните уравнения и неравенствата е, че уравненията с логаритми (например логаритъмът на 2 x = √9) предполагат една или повече конкретни числови стойности в отговора, докато при решаване на неравенството и двата диапазона на приемливи стойности и точките, нарушаващи тази функция. В резултат на това отговорът не е прост набор от отделни числа, както в отговора на уравнението, а непрекъсната серия или набор от числа.

Основни теореми за логаритмите

При решаване на примитивни задачи за намиране на стойностите на логаритъма, неговите свойства може да не са известни. Но когато става дума за логаритмични уравнения или неравенства, на първо място е необходимо ясно да се разберат и приложат на практика всички основни свойства на логаритмите. По-късно ще се запознаем с примери за уравнения, нека първо анализираме всяко свойство по-подробно.

1. Основната идентичност изглежда така: a logaB =B. Прилага се само ако a е по-голямо от 0, не е равно на единица и B е по-голямо от нула.
2. Логаритъмът на произведението може да се представи в следната формула: log d (s 1 * s 2) = log d s 1 + log d s 2. В този случай предпоставката е: d, s 1 и s 2 > 0; а≠1. Можете да дадете доказателство за тази формула от логаритми, с примери и решение. Нека log като 1 = f 1 и log като 2 = f 2 , тогава a f1 = s 1 , a f2 = s 2. Получаваме, че s 1 *s 2 = a f1 *a f2 = a f1+f2 (степенни свойства ), и по-нататък по дефиниция: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log като 2, което трябваше да се докаже.
3. Логаритъмът на частното изглежда така: log a (s 1 / s 2) = log a s 1 - log a s 2.
4. Теоремата под формата на формула приема следната форма: log a q b n = n/q log a b.

Тази формула се нарича "свойство на степента на логаритъма". Наподобява свойствата на обикновените степени и не е изненадващо, защото цялата математика се основава на редовни постулати. Нека разгледаме доказателството.

Нека log a b \u003d t, оказва се, a t = b. Ако повдигнете двете части на степен m: a tn = b n ;

но тъй като a tn = (a q) nt/q = b n , следователно log a q b n = (n*t)/t, тогава log a q b n = n/q log a b. Теоремата е доказана.

Примери за проблеми и неравенства

Най-често срещаните видове логаритмни задачи са примери за уравнения и неравенства. Те се намират в почти всички задачници, а също така са включени в задължителната част от изпитите по математика. За да влезете в университет или да преминете приемни тестове по математика, трябва да знаете как да решавате правилно такива задачи.

За съжаление няма единен план или схема за решаване и определяне на неизвестната стойност на логаритъма, но към всяко математическо неравенство или логаритмично уравнение могат да се прилагат определени правила. На първо място, трябва да разберете дали изразът може да бъде опростен или сведен до обща форма. Можете да опростите дългите логаритмични изрази, ако използвате правилно техните свойства. Да ги опознаем скоро.

При решаване на логаритмични уравнения е необходимо да се определи какъв вид логаритъм имаме пред нас: пример за израз може да съдържа естествен логаритъм или десетичен.

Ето примери ln100, ln1026. Тяхното решение се свежда до факта, че трябва да определите степента, до която основата 10 ще бъде равна съответно на 100 и 1026. За решения на естествени логаритми трябва да се прилагат логаритмични идентичности или техните свойства. Нека разгледаме примери за решаване на логаритмични задачи от различен тип.

Как да използвате логаритмни формули: с примери и решения

И така, нека разгледаме примери за използване на основните теореми за логаритмите.

1. Свойството на логаритъма на произведението може да се използва в задачи, при които е необходимо да се разложи голяма стойност на числото b на по-прости фактори. Например log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Отговорът е 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - както виждате, прилагайки четвъртото свойство на степента на логаритъма, успяхме да решим на пръв поглед сложен и неразрешим израз. Необходимо е само да се факторизира основата и след това да се извадят стойностите на степента от знака на логаритъма.

Задачи от изпита

Логаритмите често се срещат на приемните изпити, особено много логаритмични проблеми в Единния държавен изпит (държавен изпит за всички завършили училище). Обикновено тези задачи присъстват не само в част A (най-лесната тестова част от изпита), но и в част C (най-трудните и обемни задачи). Изпитът предполага точно и перфектно познаване на темата "Естествени логаритми".

Примерите и решаването на проблеми са взети от официалните версии на изпита. Нека видим как се решават подобни задачи.

Даден е log 2 (2x-1) = 4. Решение:
нека пренапишем израза, като го опростим малко log 2 (2x-1) = 2 2 , чрез дефиницията на логаритъма получаваме, че 2x-1 = 2 4 , следователно 2x = 17; х = 8,5.

• Всички логаритми се редуцират най-добре до една и съща основа, така че решението да не е тромаво и объркващо.
• Всички изрази под знака на логаритъма са посочени като положителни, следователно, когато се изважда степента на степента на израза, която е под знака на логаритъма и като негова основа, изразът, оставащ под логаритъма, трябва да бъде положителен.