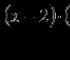Тангенс, котангенс

Дефиниции на хиперболични функции, техните области на дефиниции и стойности

ш х- хиперболичен синус
, -∞ < x < +∞; -∞ < y < +∞ .
ch x- хиперболичен косинус
, -∞ < x < +∞; 1 ≤ y< +∞ .
Мерси- хиперболичен тангенс
, -∞ < x < +∞; - 1 < y < +1 .
cth x- хиперболичен котангенс
, x ≠ 0; г< -1 или y > +1 .

Графики на хиперболични функции

График на хиперболичния синус y = ш х

График на хиперболичния косинус y = ch x

График на хиперболичния тангенс y= Мерси

График на хиперболичния котангенс y= cth x

Формули с хиперболични функции

Връзка с тригонометрични функции

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z; ch iz = cos z
tgiz = i th z ; ctg iz = - i cth z
th iz = i tg z ; cth iz = - i ctg z
Тук i е въображаема единица, i 2 = - 1 .

Прилагайки тези формули към тригонометрични функции, получаваме формули, свързващи хиперболични функции.

Паритет

sh(-x) = - sh x; ch(-x) = ch x.
th(-x) = -th x; cth(-x) = - cth x.

функция ch(x)- дори. Функции sh(x), Мерси), cth(x)- странно.

Разлика на квадратите

ch 2 x - sh 2 x = 1.

Формули за сбор и разлика на аргументи

sh(x y) = sh x ch y ch x sh y,
ch(x y) = ch x ch y sh x sh y,
,
,

sh 2 x = 2 sh x ch x,
ch 2 x = ch 2 x + sh 2 x = 2 ch 2 x - 1 = 1 + 2 sh 2 x,
.

Формули за произведения на хиперболичен синус и косинус

,
,
,

,
,
.

Формули за сбор и разлика на хиперболични функции

,
,
,
,
.

Връзка на хиперболичен синус и косинус с тангенс и котангенс

, ,
, .

Деривати

,

Интеграли от sh x, ch x, th x, cth x

,
,
.

Разширения в серии

Обратни функции

Ареасинус

При - ∞< x < ∞ и - ∞ < y < ∞ имеют место формулы:
,
.

Ареакосинус

При 1 ≤ x< ∞ И 0 ≤ y< ∞ има формули:
,
.

Вторият клон на арекосинуса се намира на 1 ≤ x< ∞ и - ∞< y ≤ 0 :
.

Повърхностна допирателна

на - 1 < x < 1 и - ∞< y < ∞ имеют место формулы:
,

Въведение

В математиката и нейните приложения към природните науки и технологиите експоненциалните функции се използват широко. Това по-специално се обяснява с факта, че много от явленията, изучавани в естествените науки, са сред така наречените процеси на органичен растеж, при които скоростите на промяна на участващите в тях функции са пропорционални на стойностите на самите функции.

Ако се означи с функция и с аргумент, тогава диференциалният закон на процеса на органичен растеж може да бъде записан във формата където е някакъв постоянен коефициент на пропорционалност.

Интегрирането на това уравнение води до общо решениекато експоненциална функция

Ако зададете начално състояниекогато, тогава е възможно да се определи произволна константа и по този начин да се намери конкретно решение, което е интегрален закон на разглеждания процес.

Процесите на органичен растеж включват, при някои опростени допускания, такива явления като например промени в атмосферното налягане в зависимост от височината над земната повърхност, радиоактивен разпад, охлаждане или нагряване на тялото в заобикаляща средапостоянна температура, едномолекулярна химическа реакция(например разтваряне на вещество във вода), при което се изпълнява законът за масовото действие (скоростта на реакцията е пропорционална на количеството на реагента), размножаването на микроорганизмите и много други.

Увеличаването на размера на парите поради начисляването на сложна лихва върху тях (лихва върху лихвата) също е процес на органичен растеж.

Тези примери могат да бъдат продължени.

Наред с отделните експоненциални функции в математиката и нейните приложения се използват различни комбинации от експоненциални функции, сред които особено значение имат някои линейни и дробно-линейни комбинации от функции и т. нар. хиперболични функции. Има шест от тези функции, за които са въведени следните специални имена и обозначения:

(хиперболичен синус),

(хиперболичен косинус),

(хиперболичен тангенс),

(хиперболичен котангенс),

(хиперболичен секанс),

(хиперболичен секанс).

Възниква въпросът защо са дадени точно такива наименования, а тук има хипербола и имената на известни от тригонометрията функции: синус, косинус и т.н.? Оказва се, че отношенията, свързващи тригонометрични функции с координатите на точки от окръжност с единичен радиус, са подобни на отношенията, свързващи хиперболични функции с координатите на точки от равностранна хипербола с единична полуос. Това оправдава името хиперболични функции.

Хиперболични функции

Функциите, дадени с формули, се наричат ​​съответно хиперболичен косинус и хиперболичен синус.

Тези функции са дефинирани и непрекъснати и е четна функция и е нечетна функция.

Фигура 1.1 - Графики на функции

От дефиницията на хиперболичните функции следва, че:

По аналогия с тригонометричните функции, хиперболичният тангенс и котангенс се определят съответно по формулите

Функция е дефинирана и непрекъсната върху, а функция е дефинирана и непрекъсната върху множество с пунктирана точка; и двете функции са странни, техните графики са показани на фигурите по-долу.

Фигура 1.2 - Графика на функцията

Фигура 1.3 - Графика на функцията

Може да се покаже, че функциите и са строго нарастващи, докато функцията е строго намаляваща. Следователно тези функции са обратими. Обратните към тях функции означаваме съответно с.

Помислете за функция, обратна на функция, т.е. функция. Изразяваме го с елементарни. Решавайки уравнението по отношение на, получаваме Тъй като, тогава откъде

Заменяйки с и с, намираме формулата за обратната функция за хиперболичния синус.

Наред с връзката между тригонометричните и експоненциални функции(формули на Ойлер)

в сложната област има такава много проста връзкамежду тригонометрични и хиперболични функции.

Припомнете си, че според определението:

Ако в тъждеството (3) заменим до тогава от дясната страна получаваме същия израз, който е от дясната страна на тъждеството, от което следва равенството на левите страни. Същото важи и за тъждествата (4) и (2).

Разделяйки двете части на идентичността (6) на съответните части на идентичността (5) и обратно (5) чрез (6), получаваме:

Подобна замяна в идентичности (1) и (2) и сравнение с идентичности (3) и (4) дава:

И накрая, от идентичностите (9) и (10) намираме:

Ако поставим идентичности (5)-(12), където x е реално число, т.е. считаме аргумента чисто въображаем, тогава получаваме още осем идентичности между тригонометричните функции на чисто въображаем аргумент и съответните хиперболични функции на реален аргумент, както и между хиперболичните функции на чисто въображаем аргумент и съответните тригонометрични функции на реален аргумент:

Получените отношения позволяват преминаването от тригонометрични функциидо хиперболичен и от

хиперболични функции към тригонометрични със замяната на имагинерния аргумент с реалния. Те могат да бъдат формулирани като следното правило:

За да преминете от тригонометрични функции на въображаем аргумент към хиперболични или, обратно, от хиперболични функции на въображаем аргумент към тригонометрични, трябва да извадите въображаемата единица от функционалния знак за синуса и тангенса и да я изхвърлите напълно за косинуса.

Установената връзка е забележителна по-специално с това, че позволява да се получат всички отношения между хиперболични функции от известни отношения между тригонометрични функции чрез заместване на последните с хиперболични функции

Нека покажем как е. се прави.

Вземете за пример основната тригонометрична идентичност

и поставете в него, където x е реално число; получаваме:

Ако в това тъждество заместим синуса и косинуса с хиперболичния синус и косинус съгласно формулите, тогава получаваме или и това е основното тъждество между предварително получените по различен начин.

По същия начин можете да изведете всички други формули, включително формули за хиперболичните функции на сумата и разликата на аргументите, двойни и половин аргументи и т.н., като по този начин от обикновената тригонометрия получавате "хиперболична тригонометрия".