Кои са признаците, че триъгълниците са равни? Първият знак за равенство на триъгълниците

Геометрична фигура, образувана от три отсечки, които свързват три точки, които не принадлежат на една и съща права линия.

Страните на триъгълника образуват три ъгъла във върховете на триъгълника. Перифразирайки, триъгълнике многоъгълник, който има три ъгъла .

Практическо значение признаци за равенство на триъгълницисе свежда до следното: според формулировката триъгълниците са равни, в случай че е възможно да се наслагват един върху друг, така че да съвпадат; прилагането на триъгълно припокриване обаче понякога може да бъде трудно, а понякога и невъзможно.

Тестовете за равенство на триъгълници позволяват да се замени припокриването на триъгълници чрез намиране и сравняване на отделни основни компоненти (страни и ъгли) и по този начин да се обоснове равенството на триъгълниците.

3. И трите страни:

Те също подчертават четвърти знак, който не е толкова широко обхванат в училищния курс по математика, колкото предишните три. Формулира се по следния начин:

Ако две страни на първия триъгълник са съответно равни на две страни на втория триъгълник и ъгълът срещу по-голямата от тези страни в първия триъгълник е равен на ъгъла срещу съответната страна, равна на него във втория триъгълник, тогава тези триъгълниците са равни.

Признаци за равенство на триъгълници

Триъгълници, чиито страни са равни, се наричат равни.

Теорема (първият признак за равенство на триъгълниците).
Ако две страни и ъгълът между тях на един триъгълник са съответно равни на две страни и ъгълът между тях на друг триъгълник, тогава тези триъгълници са еднакви.

Теорема (втори критерий за равенство на триъгълници).
Ако страна и два съседни ъгъла на един триъгълник са съответно равни на страна и два съседни ъгъла на друг триъгълник, тогава тези триъгълници са еднакви.

Теорема (трети критерий за равенство на триъгълници).
Ако три страни на един триъгълник са съответно равни на три страни на друг триъгълник, тогава тези триъгълници са еднакви.

Признаци за подобие на триъгълници

Триъгълници, чиито ъгли са равни и чиито еднакви страни са пропорционални, се наричат подобни: , където е коефициентът на подобие.

I знак за подобие на триъгълници.Ако два ъгъла на един триъгълник са съответно равни на два ъгъла на друг, тогава тези триъгълници са подобни.

II признак за подобие на триъгълници.Ако три страни на един триъгълник са пропорционални на три страни на друг триъгълник, тогава триъгълниците са подобни.

III признак за подобие на триъгълници.Ако две страни на един триъгълник са пропорционални на две страни на друг триъгълник и ъглите между тези страни са равни, тогава триъгълниците са подобни.

1) на двете страни и ъгъла между тях

Доказателство:

Нека триъгълниците ABC и A 1 B 1 C 1 имат ъгъл A, равен на ъгъл A 1, AB равен на A 1 B 1, AC равен на A 1 C 1. Нека докажем, че триъгълниците са еднакви.

Нека наложим триъгълник ABC (или симетрично на него)върху триъгълник A 1 B 1 C 1, така че ъгъл A да е подравнен с ъгъл A 1 . Тъй като AB=A 1 B 1 и AC=A 1 C 1, тогава B ще съвпада с B 1, а C ще съвпада с C 1. Това означава, че триъгълник A 1 B 1 C 1 съвпада с триъгълник ABC и следователно е равно на триъгълник ABC.

Теоремата е доказана.

2) по страничните и съседните ъгли

Доказателство:

Нека ABC и A 1 B 1 C 1 са два триъгълника, в които AB е равен на A 1 B 1, ъгъл A е равен на ъгъл A 1 и ъгъл B е равен на ъгъл B 1. Нека докажем, че са равни.

Нека наложим триъгълник ABC (или симетрично на него)върху триъгълника A 1 B 1 C 1, така че AB съвпада с A 1 B 1. Тъй като ∠BAC =∠B 1 A 1 C 1 и ∠ABC=∠A 1 B 1 C 1, то лъч AC ще съвпада с A 1 C 1 и BC ще съвпадне с B 1 C 1. От това следва, че връх C съвпада с C 1. Това означава, че триъгълник A 1 B 1 C 1 съвпада с триъгълник ABC и следователно е равен на триъгълник ABC.

Теоремата е доказана.

3) от три страни

Доказателство:

Да разгледаме триъгълници ABC и A l B l C 1, в които AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Нека докажем, че ΔАВС =ΔA 1 B 1 C 1.

Нека приложим триъгълник ABC (или симетрично на него)към триъгълника A 1 B 1 C 1, така че връх A е подравнен с връх A 1, връх B е подравнен с връх B 1, а върховете C и C 1 са на противоположните страни на правата A 1 B 1. Нека разгледаме 3 случая:

1) Лъч C 1 C минава в ъгъла A 1 C 1 B 1. Тъй като според условията на теоремата страните AC и A 1 C 1, BC и B 1 C 1 са равни, тогава триъгълниците A 1 C 1 C и B 1 C 1 C са равнобедрени. По теоремата за свойството на ъглите на равнобедрен триъгълник ∠1 = ∠2, ∠3 = ∠4, следователно ∠ACB=∠A 1 C 1 B 1 .

2) Лъч C 1 C съвпада с една от страните на този ъгъл. A лежи на CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - равнобедрен, ∠ACB=∠A 1 C 1 B 1.

3) Лъч C 1 C минава извън ъгъла A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, което означава ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

И така, AC=A 1 C 1, BC=B 1 C 1, ∠C=∠C 1. Следователно триъгълниците ABC и A 1 B 1 C 1 са равни
първият критерий за равенство на триъгълниците.

Теоремата е доказана.

2. Разделяне на отсечка на n равни части.

Начертайте лъч през А, очертайте n равни сегмента върху него. Начертайте права линия през B и A n и успоредни на нея през точки A 1 - A n -1. Нека отбележим техните пресечни точки с AB. Получаваме n отсечки, които са равни според теоремата на Талес.

Теорема на Талес. Ако няколко равни сегмента са разположени последователно на една от двете линии и през краищата им са начертани успоредни линии, които пресичат втората линия, тогава те ще отрежат равни сегменти на втората линия.

Доказателство. AB=CD

1. Начертайте прави линии през точки A и C, успоредни на другата страна на ъгъла. Получаваме два успоредника AB 2 B 1 A 1 и CD 2 D 1 C 1. Според свойството на успоредник: AB 2 = A 1 B 1 и CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 и са равни въз основа на втория критерий за равенство на триъгълниците:
AB = CD съгласно теоремата,
като съответни, образувани в пресечната точка на успоредник BB 1 и DD 1 права линия BD.

3. По същия начин всеки от ъглите се оказва равен на ъгъла с върха в точката на пресичане на секущите. AB 2 = CD 2 като съответни елементи в еднакви триъгълници.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Подгорни Максим

Материалът от изследователската работа може да се използва за кръжоци по геометрия в 7. клас

Изтегли:

Преглед:

MBU DO на град Ростов на Дон "Дворец на творчеството на децата и младежта"

Донска академия на науките за млади изследователи, кръстена на. Ю. А. Жданова

Математика

Тема: “Нестандартни теореми за равенството на триъгълници”

Подгорни Максим, 7 клас,

MBOU средно училище № 3,

Ръководител:

Олейникова Людмила Александровна,

учител по математика,

MBOU средно училище № 3,

Салск, Ростовска област

Ростов на Дон

2017 г

Въведение……………………………………………………………………………3

Главна част

Признаци за равенство на триъгълници……………………………………………… 4

Нестандартни знаци за равенство на триъгълници………………………….7

Заключение………………………………………………………………………………… 10

Използвана литература……………………………………………………………… 11

Приложение

Въведение.

Уместност:

Триъгълникът е една от основните фигури в планиметрията. Чух много от гимназисти, че когато се подготвят за Единния държавен изпит, често трябва да доказват равенството на триъгълници. И познаването на основните знаци се оказва недостатъчно. Исках да знам дали е възможно да се докаже равенството на триъгълници с други параметри. В учебника по геометрия, от който учат учениците на нашето училище (автори Л. С. Атанасян, В. Ф. Бутузов и др. Геометрия 7-9), се разглеждат само 3 знака за равенство на триъгълници. Прегледах учебни комплекти от други автори. Но дори и в тях са предложени за изучаване само три добре известни теореми.

Хипотеза:

Възможно ли е да се формулират, освен трите добре познати, други критерии за равенство на триъгълниците?

За да се уверя, че отговорът на този въпрос засяга не само мен, проведох социологическо проучване сред ученици от 7-11 клас (виж Приложение 1).

Предположенията ми се потвърдиха. Повечето ученици знаят само три признака, че триъгълниците са равни.

Така че целта на моето изследване беше да намеря нови признаци за равенство на триъгълници.

Задачи:

ΘПроучете литературата по изучаваната тема.

ΘПосочете броя на признаците, че триъгълниците са равни.

ΘДемонстрирайте на вашите съученици и ученици от нашето училище съществуването на други признаци на равенство на триъгълници и възможността за тяхното доказване.

Обект на изследване:

Изучаване на признаците за равенство на триъгълници.

Предмет на изследване. Триъгълникът е една от основните фигури в планиметрията.

Изследователски метод:Теоретичен (проучване, анализ и синтез), системно-търсен, практически (доказателство на теореми).

Историческа справка

Триъгълникът е една от централните фигури на цялата геометрия.

При решаването на задачи се използва голямото му разнообразие от свойства.

Свойствата на триъгълника се използват широко в практиката: в архитектурата; при разработване на чертеж на сграда, при планиране на бъдещи апартаменти; в индустрията, в проектирането на различни части, в производството на строителни материали, в строителството на кораби и самолети; в навигацията за начертаване на правилен и най-точен маршрут; в астрологията и астрономията триъгълникът е много значима фигура; Триъгълниците правят конструкциите на високоволтови електропроводи и железопътни мостове надеждни.

Освен това има много други области, в които се използват различни свойства на триъгълника: когато започвате игра на билярд, трябва да подредите топките под формата на триъгълник, за това те използват специално устройство; поставянето на кеглите в играта боулинг също е под формата на равностранен триъгълник; триъгълниците се използват за създаване на красиви паркети; устройство на триъгълника на Паскал: всяко число е равно на сумата от двете числа, разположени над него (оградете трите числа с триъгълник). Всичко е елементарно, но колко чудеса се крият в него! Компютърът преведе триъгълника на Паскал на езика на цветовете.

Темата за триъгълника може да бъде продължена за неопределено време.

В света има толкова много триъгълници!

Има и фигуративни значения на тази фигура: например правилото на „златния триъгълник“ се основава на психологията на купувача - след като намери продукта, от който се нуждае, купувачът се втурва към касата. Задачата на продавачите е да го накарат да остане в магазина по-дълго, като постави стоките, от които се нуждае купувачът, във върховете на въображаем триъгълник, тоест да „закотви“ купувача. Колкото по-голяма е площта на триъгълника, толкова по-успешно може да се нарече оформлението на магазина. В магазин за хранителни стоки тези основни продукти са гастрономия, млечни продукти и хляб. Задната крайна стена на търговската зона е второто по важност място и там е най-препоръчително да поставите анкерни продукти - именно за да принудите купувача да премине през целия периметър на магазина.

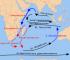
Добре известният Бермудски триъгълник е зона в Атлантическия океан, където се случват предполагаеми мистериозни изчезвания на кораби и самолети. Районът е ограничен от линии от Флорида до Бермудите, до Пуерто Рико и обратно до Флорида през Бахамските острови.

Следователно изучаването на триъгълник и всички негови свойства е много актуална тема.

Целта на тази работа е да говорим за признаците на равенство на триъгълниците, което е едно от най-важните им свойства.

Тестове за равенство на триъгълници са теореми, въз основа на които може да се докаже, че някоитриъгълници са равни.

В геометрията се използват три знака за равенство на триъгълниците.

Тази тема е практически изучавана, тъй като днес има три критерия за равенство на триъгълници, които могат да бъдат доказани с помощта на съответните теореми.

В древността заедно с астрономията се появява и науката тригонометрия. Думата "тригонометрия" произлиза от гръцките "триъгълник" и "мярка". Буквалното значение е „наука за измерване на триъгълници“.

Използвайки опънати въжета с дължина 3, 4 и 5 единици, египетските жреци са получавали прави ъгли при изграждане на храмове и др.

Изкуството да се изобразяват предмети върху плоскост привлича вниманието на хората от древни времена; хората рисуват различни орнаменти, растения и животни върху скали, стени, съдове и други битови предмети. Хората се стремяха да гарантират, че изображението правилно отразява естествената форма на обекта.

Учението за подобието на фигурите, основано на теорията за отношенията и пропорциите, е създадено в Древна Гърция през 5-4 век пр. н. е. и съществува и се развива и до днес. Например, има много детски играчки, подобни на артикулите в света на възрастните, обувки и дрехи от същия стил се предлагат в различни размери. Тези примери могат да бъдат продължени по-нататък. В крайна сметка всички хора си приличат и, както се казва в Библията, Бог ги е създал по свой образ и подобие.

Тестовете за равенство на триъгълници отдавна са от голямо значение в геометрията, тъй като доказателството на многобройни теореми се свежда до доказване на равенството на определени триъгълници. Питагорейците вече са били ангажирани с доказването на знаците за равенство на триъгълниците. Според Прокъл Евдем от Родос приписва на Талес от Милет доказателство за равенството на два триъгълника с равни страни и два ъгъла, съседни на него (вторият знак за равенството на триъгълниците).

Талес използва тази теорема, за да определи разстоянието от брега до морските кораби.Не е известно какъв точно метод е използвал Талес за това.

Признаци за равенство на триъгълници.

Да започнем с определение. Триъгълниците ABC и A1B1C1 се наричат равни, ако могат да се комбинират чрез припокриване.

Триъгълникът се състои от шест елемента: три ъгъла и три страни.

Това повдига въпроса: „Какъв е най-малкият брой триъгълни елементи, необходими за установяване на равенството на два триъгълника?“

Няма да можем да установим равенството на два триъгълника въз основа на един елемент, защото не е известно: „Останалите елементи ще бъдат ли равни?“

Също така е невъзможно да се установи равенството на два триъгълника с помощта на два елемента поради липсата на информация за установяване на равенството.

Възможно е да се установи равенството на два триъгълника с помощта на три елемента. Но това повдига въпроса: „Кои точно три елемента трябва да бъдат назовани, за да се установи равенството на триъгълниците?“

Когато изучавах този въпрос, прегледах училищните учебници по геометрия на различни автори, както и речници и справочници. В учебниците за седми клас са предложени за изучаване само три критерия за равенство на триъгълниците.

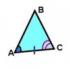
Θ1 Знак : Ако две страни и ъгълът между тях на един триъгълник са съответно равни на две страни и ъгълът между тях на друг триъгълник, тогава тези триъгълници са еднакви. Фиг. 1

Доказателство. Помислете за триъгълници ABC и A 1 B 1 C 1 , (фиг. 1), за които AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 . Нека докажем, че ΔABC = ΔA 1 B 1 C 1 .

Тъй като ∠A = ∠A 1 , тогава триъгълник ABC може да бъде насложен върху триъгълник A 1 B 1 C 1 така че връх А да съвпада с връх А 1 , а страните AB и AC ще припокриват съответно лъчите A 1 B 1 и A 1 C 1 . Тъй като AB = A 1 B 1, AC = A 1 C 1 , тогава страна AB ще се подравни със страна A 1 в 1 и страна AC е със страна A 1 C 1 ; по-специално, точки B и B ще съвпадат 1, C и C 1 . Следователно страните BC и B ще съвпадат 1 C 1 . И така, триъгълници ABC и A 1 B 1 C 1 са напълно съвместими, което означава, че са равни.

И ето как първият знак за равенство на триъгълниците е бил използван в Древен Египет (от двете страни и ъгъла между тях), Талес от Милет също се смята за негов създател, за да измери височината на пирамидата: представете си, че стоим пред огромна пирамида, как можем да измерим нейната височина? В крайна сметка не можете да прикачите измервателни уреди към него! И тук първият знак за равенство на триъгълниците идва на помощ на Талес от Милет: той изчака, докато сянката му съвпадне точно с височината му, приложи теоремата, оказа се, че височината на пирамидата е равна на нейната сянка (фиг. 2).

Ориз. 2

Θ2 знак: Ако страна и два съседни ъгъла на един триъгълник са съответно равни на страна и два съседни ъгъла на друг триъгълник, тогава тези триъгълници са еднакви.

Доказателство: Ако в △ABC и △A 1 B 1 C 1 ще се случат следните равенства AB=A 1 B 1, ∠BAC=∠B 1 A 1 C 1, ∠АВС= ∠А 1 B 1 C 1 . Нека поставим триъгълници А един върху друг 1 B 1 C 1 и ABC така, че равните страни AB и A съвпадат 1 в 1 и ъглите, които са в съседство с тях. Както в предишния вече обсъден пример, ако е необходимо, триъгълник A 1 B 1 C 1 Можете да го „обърнете и да го поставите от другата страна“. Триъгълниците ще съвпадат, следователно могат да се считат за равни.

Θ3 Знак : Ако три страни на един триъгълник са съответно равни на три страни на друг триъгълник, тогава тези триъгълници са еднакви. Доказателство: Нека за △ABC и △A 1 B 1 C 1 равенства А са валидни 1 B 1 = AB, B 1 C 1 = BC, C 1 A 1 = SA. Нека преместим триъгълник A 1 B 1 C 1 така че тази страна А 1 в 1 съвпада със страна AB и връх B 1 и Б, А 1 и А ще съвпадат. Вземете окръжност с център A и радиус AC и втора окръжност с център B и радиус BC. Тези окръжности ще се пресичат в две точки, симетрични по отношение на сегмента AB: точка C и точка C 2 . Това означава, че C1, след като премести триъгълника A1B1C1, трябва да съвпадне или с точки C, или с C2. Във всеки случай това ще означава равенството △ABC=△A 1 B 1 C 1 , тъй като триъгълници △ABC=△ABC 2 са равни (в края на краищата тези триъгълници са симетрични спрямо сегмента AB.

Това свойство - твърдостта на триъгълника - се използва широко в практиката. Така че, за да се закрепи стълбът във вертикално положение, върху него се поставя опора; същият принцип се използва при монтажа на скобата.

Свойството триъгълна твърдост се използва широко в практиката при изграждането на железни конструкции.

От третия критерий за равенство на триъгълниците следва, че триъгълникът е твърда фигура. Защото: можем да си представим две летви, двата края на които са закрепени с пирон. Този дизайн не е твърд, но чрез преместване или разпръскване на свободните краища на ламелите можем да променим ъгъла между тях. Сега нека вземем друга летва и затегнем краищата й със свободните краища на първите две летви. Получената структура - триъгълник - вече ще бъде твърда. Невъзможно е да преместите или раздалечите две страни, т.е. нито един ъгъл не може да бъде променен. Наистина, ако това беше възможно, тогава щяхме да получим нов триъгълник, който да не е равен на първоначалния. Но това е невъзможно, тъй като новият триъгълник трябва да е равен на оригиналния в третия

В справочника по елементарна математика на М. Я. Выгодски намерих друг знак.

Θ4 Знак: Ако две страни и ъгълът срещу по-големия от един триъгълник са съответно равни на две страни и ъгълът срещу по-големия от друг триъгълник, тогава такива триъгълници са еднакви.

Ще докажа този знак.

дадени : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1,∠ B= ∠ B1

Докажете: ΔABC=A1B1C1.

Нека подредим триъгълниците, както е на фигура 1. Нека свържем B и B1, след това ΔАВВ1

Равнобедрен означава∠ 1= ∠ 2. ∠ 3= ∠ 4 като остатъци от равни ъгли.

Получаваме ΔВСВ1 - равнобедрен, откъдето ВС=В1С1. ΔАВС = ΔА1В1С1 от трите страни.

Също така в училищния курс се обсъждат 4 знака за равенство на правоъгълни триъгълници:

Θ1 . Ако катетите на един правоъгълен триъгълник са съответно равни на катетите на друг, тогава такива триъгълници са еднакви.

Θ2 . Ако катетът и прилежащият остър ъгъл на един правоъгълен триъгълник са съответно равни на катета и прилежащия остър ъгъл на друг, тогава такива триъгълници са еднакви.

Θ3 . Ако хипотенузата и острия ъгъл на един правоъгълен триъгълник са съответно равни на хипотенузата и острия ъгъл на друг, тогава такива триъгълници са еднакви.

Θ4 . Ако хипотенузата и катетът на един правоъгълен триъгълник са съответно равни на хипотенузата и катетът на друг, тогава тези триъгълници са еднакви.

Реших теоретичната основа на критериите за равенство на триъгълници, като добавих други компоненти към страните и ъглите, използвани в класическите тестове за равенство на триъгълници: ъглополовяща, медиана и височина.

Нестандартни критерии за съответствие на триъгълници.

1) На две страни и височината, начертана към едната от тях.

Дадено е: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔABK=ΔA1B1K1 чрез хипотенуза и катет, тогава∠ B= ∠ B1 и получаваме ΔABC= ΔA1B1C1 според първия знак.

2) На две страни и медиана, начертана към едната от тях

Дадено е: AB=A1B1, BC=B1C1, AK=A1K1, AK и A1K1 са медиани.

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔABK=ΔA1B1K1 от трите страни, което означава∠ B= ∠ B1 и ΔABC= ΔA1B1C1 според първия знак.

3) По двете страни и височина, изтеглена от третия ъгъл.

Дадено е: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔABK=ΔA1B1K1 по крака и остър ъгъл, което означава BK=B1K1,

ΔACK=ΔA1C1K1 по катет и остър ъгъл, което означава KC=K1C1, следователно BC=B1C1, и ΔABC= ΔA1B1C1 по втория знак.

4) По една страна и две височини, изтеглени от ъглите, съседни на тази страна.

Дадено е: AC=A1C1, SM=C1M1, AK=A1K1.

Докажете: ΔСC= ΔA1B1C1.

Доказателство: ΔAMC= ΔA1М1C1 по катета и хипотенузата, което означава∠ A= ∠ A1, а ΔAКC= ΔA1К1C1 по катета и хипотенузата, т.е.∠ C= ∠ C1.

И така, ΔABC= ΔA1B1C1 според втория критерий.

5) От двете страни и височината, начертана към третата страна.

дадени: AB=A1B1,BC=B1C1,BK=B1K1.

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔABK=ΔA1B1K1 на хипотенузата и крака, което означава AK=A1K1,

ΔBКC= ΔB1К1C1 по катета и хипотенузата, което означава KC=K1C1.

И така, ΔABC= ΔA1B1C1 от трите страни.

6) По протежение на страната, един от ъглите, съседни на тази страна, и ъглополовящата от този ъгъл.

Дадено е: AC=A1C1, AK=A1K1,∠ A ∠ A1.

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔКАС=ΔК1А1С1 по първия знак, което означава∠ C= ∠ C1,

ΔABC= ΔA1B1C1 по втората характеристика.

7) По две височини и ъгъла, от който е начертана една от височините.

Дадено е: SM=S1M1, AK=A1K1, ∠ A ∠ A1.

Докажете: ΔABC= ΔA1B1C1.

Доказателство: ΔAMC= ΔA1М1C1 по катет и остър ъгъл, ΔКАС=ΔК1А1С1 по катет и хипотенуза, ΔABC= ΔA1B1C1 по втори знак.

Заключение.

По време на изследването разбрах, че в допълнение към трите основни признака на равенство на триъгълниците е възможно да се посочат много други. Формулирах и доказах равенството на триъгълниците въз основа на медианата, надморската височина, ъглополовящата на триъгълника в комбинация със страните и ъглите на триъгълника, като се придържах към наличието на три елемента. Сега мога да кажа на учениците от нашето училище, че има и други признаци, че триъгълниците са равни. Това ще позволи на завършилите училище да прилагат резултатите от моите изследвания в подготовката за Единния държавен изпит и Единния държавен изпит и лесно да решават геометрични задачи, използвайки тези функции.

Резултатът от моите изследвания: Доказани са няколко критерия за равенство на триъгълници, които не се изучават в училищния курс по геометрия.

Библиография

Вигодски М.Я. Наръчник по елементарна математика.
Геометрия. 7-9 клас: учебник. За общо образование институции/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19 изд. – М.: Образование, 2009.
Погорелов А.В. Геометрия: Учебник. За 7-9 клас. общо образование институции. – 3-то издание. – М.: Образование, 2002.
. Енциклопедия "Аванта" по математика, Москва, 2004 г.
2. Уикипедия е безплатна енциклопедия.
3. Глейзър Г.И. „История на математиката в училище“, Москва, Просвещение, 1982 г.
4. Гусева Т.М. Признаци на подобие на триъгълници - Москва, 1 септември, приложение "Математика", 1999 г., № 28
5. Погорелов А.В. "Геометрия 7-9 клас"Москва, Образование, 2003 г

Приложение 1

1. Колко признака смятате, че триъгълниците са равни?

A) 3 B) повече от три C) по-малко от три

2. Искате ли да научите нови признаци за съответствие на триъгълници?

А) да Б) не

Два триъгълника се наричат еднакви, ако могат да бъдат събрани чрез припокриване. Фигура 1 показва еднакви триъгълници ABC и A 1 B 1 C 1. Всеки от тези триъгълници може да бъде насложен върху другия, така че да са напълно съвместими, тоест върховете и страните им да съвпадат по двойки. Ясно е, че ъглите на тези триъгълници също ще съвпадат по двойки.

Така, ако два триъгълника са еднакви, тогава елементите (т.е. страни и ъгли) на единия триъгълник са съответно равни на елементите на другия триъгълник. Забележи, че в равни триъгълници срещу съответно равни страни(т.е. припокриване при наслагване) лежат равни ъглии обратно: Равните страни лежат срещу съответно равни ъгли.

Така например в равни триъгълници ABC и A 1 B 1 C 1, показани на фигура 1, срещу равни страни AB и A 1 B 1, съответно, лежат равни ъгли C и C 1. Ще обозначим равенството на триъгълниците ABC и A 1 B 1 C 1, както следва: Δ ABC = Δ A 1 B 1 C 1. Оказва се, че равенството на два триъгълника може да се установи чрез сравняване на някои от техните елементи.

Теорема 1. Първият знак за равенство на триъгълниците.Ако две страни и ъгълът между тях на един триъгълник са съответно равни на две страни и ъгълът между тях на друг триъгълник, тогава такива триъгълници са еднакви (фиг. 2).

Доказателство. Да разгледаме триъгълници ABC и A 1 B 1 C 1, в които AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (виж Фиг. 2). Нека докажем, че Δ ABC = Δ A 1 B 1 C 1 .

Тъй като ∠ A = ∠ A 1, тогава триъгълник ABC може да бъде насложен върху триъгълник A 1 B 1 C 1 така, че върхът A да е подравнен с върха A 1, а страните AB и AC са съответно насложени върху лъчите A 1 B 1 и A 1 C 1 . Тъй като AB = A 1 B 1, AC = A 1 C 1, тогава страната AB ще се изравни със страната A 1 B 1 и страната AC ще се изравни със страната A 1 C 1; по-специално, точки B и B 1, C и C 1 ще съвпадат. Следователно страните BC и B 1 C 1 ще съвпадат. И така, триъгълниците ABC и A 1 B 1 C 1 са напълно съвместими, което означава, че са равни.

Теорема 2 се доказва по подобен начин с помощта на метода на суперпозицията.

Теорема 2. Вторият знак за равенство на триъгълниците.Ако страна и два съседни ъгъла на един триъгълник са съответно равни на страната и два съседни ъгъла на друг триъгълник, тогава тези триъгълници са равни (фиг. 34).

Коментирайте. Въз основа на теорема 2 е установена теорема 3.

Теорема 3. Сборът от всеки два вътрешни ъгъла на триъгълник е по-малък от 180°.

Теорема 4 следва от последната теорема.

Теорема 4. Външен ъгъл на триъгълник е по-голям от всеки вътрешен ъгъл, който не е съседен на него.

Теорема 5. Третият знак за равенство на триъгълниците.Ако три страни на един триъгълник са съответно равни на три страни на друг триъгълник, тогава такива триъгълници са еднакви ().

Пример 1.В триъгълници ABC и DEF (фиг. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm. Какъв ъгъл в триъгълник DEF е равен на ъгъл B?

Решение. Тези триъгълници са равни по първия знак. Ъгъл F на триъгълник DEF е равен на ъгъл B на триъгълник ABC, тъй като тези ъгли лежат срещу съответно равни страни DE и AC.

Пример 2.Отсечките AB и CD (фиг. 5) се пресичат в точка O, която е средата на всеки от тях. Каква е дължината на отсечката BD, ако отсечката AC е 6 m?

Решение. Триъгълниците AOC и BOD са равни (според първия критерий): ∠ AOC = ∠ BOD (вертикално), AO = OB, CO = OD (по условие).
От равенството на тези триъгълници следва, че страните им са равни, т.е. AC = BD. Но тъй като според условието AC = 6 m, тогава BD = 6 m.