علائم مساوی بودن مثلث ها چیست؟ اولین علامت برابری مثلث ها

شکل هندسی که از سه قسمت تشکیل شده است که سه نقطه را که به یک خط مستقیم تعلق ندارند به هم متصل می کند.

اضلاع مثلث سه زاویه را در رأس مثلث تشکیل می دهند. به تعبیر، مثلثچند ضلعی است که سه زاویه دارد .

اهمیت عملی نشانه های برابری مثلث هابه موارد زیر خلاصه می شود: با توجه به عبارت مثلث ها مساوی هستنددر مواردی که امکان قرار دادن آنها بر یکدیگر وجود داشته باشد تا با هم منطبق شوند. با این حال، اجرای همپوشانی مثلث گاهی می‌تواند دشوار و گاهی غیرممکن باشد.

آزمایش‌های تساوی مثلث‌ها، جایگزینی همپوشانی مثلث‌ها را با یافتن و مقایسه اجزای اساسی منفرد (اضلاع و زوایا) ممکن می‌سازد و در نتیجه تساوی مثلث‌ها را توجیه می‌کند.

3. هر سه طرف:

آنها نیز برجسته می کنند علامت چهارم، که در درس ریاضی مدرسه به اندازه سه دوره قبلی به طور گسترده ای پوشش داده نمی شود. به صورت زیر فرموله شده است:

اگر دو ضلع از مثلث اول به ترتیب برابر با دو ضلع مثلث دوم و زاویه مقابل بزرگتر از این ضلع ها در مثلث اول برابر با زاویه مقابل ضلع مربوطه برابر با آن در مثلث دوم باشد، این مثلث ها مساوی هستند.

نشانه های برابری مثلث ها

به مثلث هایی که اضلاع متناظر آنها با هم مساوی است، همگن می گویند.

قضیه (نخستین علامت تساوی مثلث ها).
اگر دو ضلع و زاویه بین یک مثلث به ترتیب برابر با دو ضلع و زاویه بین آنها با مثلث دیگر باشد، این مثلث ها متجانس هستند.

قضیه (معیار دوم برای تساوی مثلث ها).
اگر یک ضلع و دو زاویه مجاور یک مثلث به ترتیب با یک ضلع و دو زاویه مجاور یک مثلث دیگر برابر باشند، این مثلث ها متجانس هستند.

قضیه (ملاک سوم برای تساوی مثلث ها).
اگر سه ضلع یک مثلث به ترتیب برابر با سه ضلع مثلث دیگر باشد، این مثلث ها متجانس هستند.

علائم تشابه مثلث ها

به مثلث هایی که زوایای آنها مساوی و اضلاع مشابه آنها متناسب است، مشابه می گویند: ، ضریب شباهت کجاست.

من نشانه شباهت مثلث ها هستم.اگر دو زاویه از یک مثلث به ترتیب برابر با دو زاویه از مثلث دیگر باشند، این مثلث ها مشابه هستند.

علامت دوم شباهت مثلث ها.اگر سه ضلع یک مثلث با سه ضلع مثلث دیگر متناسب باشد، مثلث ها شبیه هم هستند.

علامت سوم شباهت مثلث ها.اگر دو ضلع یک مثلث با دو ضلع مثلث دیگر متناسب باشد و زوایای بین این ضلع ها مساوی باشد، مثلث ها شبیه هم هستند.

1) در دو طرف و زاویه بین آنها

اثبات:

فرض کنید مثلث های ABC و A 1 B 1 C 1 دارای زاویه A برابر با زاویه A 1، AB برابر با A 1 B 1، AC برابر با A 1 C 1 باشند. بیایید ثابت کنیم که مثلث ها متجانس هستند.

بیایید مثلث ABC را تحمیل کنیم (یا متقارن با آن)روی مثلث A 1 B 1 C 1 به طوری که زاویه A با زاویه A 1 تراز شود. از آنجایی که AB=A 1 B 1، و AC=A 1 C 1، پس B با B 1 منطبق خواهد شد و C با C 1 منطبق خواهد شد. این بدان معناست که مثلث A 1 B 1 C 1 با مثلث ABC منطبق است، و بنابراین برابر مثلث ABC

قضیه ثابت می شود.

2) در امتداد کناره ها و گوشه های مجاور

اثبات:

فرض کنید ABC و A 1 B 1 C 1 دو مثلث باشند که در آنها AB برابر با A 1 B 1، زاویه A برابر با زاویه A 1 و زاویه B برابر با زاویه B 1 است. بیایید ثابت کنیم که آنها برابر هستند.

بیایید مثلث ABC را تحمیل کنیم (یا متقارن با آن)روی مثلث A 1 B 1 C 1 به طوری که AB با A 1 B 1 منطبق است. از آنجایی که ∠BAC =∠B 1 A 1 C 1 و ∠ABC=∠A 1 B 1 C 1، پس پرتو AC با A 1 C منطبق خواهد شد. 1 و BC با B 1 C 1 منطبق خواهد شد. نتیجه این است که راس C با C 1 منطبق است. این بدان معنی است که مثلث A 1 B 1 C 1 با مثلث ABC منطبق است و بنابراین برابر با مثلث ABC است.

قضیه ثابت می شود.

3) در سه طرف

اثبات:

مثلث های ABC و A l B l C 1 را در نظر بگیرید که در آنها AB = A 1 B 1، BC = B l C 1 CA = C 1 A 1. اجازه دهید ثابت کنیم که ΔАВС =ΔA 1 B 1 C 1.

بیایید مثلث ABC را اعمال کنیم (یا متقارن با آن)به مثلث A 1 B 1 C 1 به طوری که راس A با راس A 1، راس B با راس B 1 و رئوس C و C 1 در اضلاع مخالف خط مستقیم A 1 B 1 قرار دارند. بیایید 3 مورد را در نظر بگیریم:

1) پرتو C 1 C از داخل زاویه A 1 C 1 B 1 می گذرد. از آنجایی که طبق شرایط قضیه، اضلاع AC و A 1 C 1، BC و B 1 C 1 برابر هستند، پس مثلث های A 1 C 1 C و B 1 C 1 C متساوی الساقین هستند. با قضیه خاصیت زوایای مثلث متساوی الساقین، ∠1 = ∠2، ∠3 = ∠4، بنابراین ∠ACB=∠A 1 C 1 B 1 .

2) اشعه C 1 C با یکی از اضلاع این زاویه منطبق است. یک دروغ در CC 1. AC=A 1 C 1، BC=B 1 C 1، C 1 BC - متساوی الساقین، ∠ACB=∠A 1 C 1 B 1.

3) پرتو C 1 C از زاویه A 1 C 1 B 1 خارج می شود. AC=A 1 C 1، BC=B 1 C 1، یعنی ∠1 = ∠2، ∠1+∠3 = ∠2+∠4، ∠ACB=∠A 1 C 1 B 1.

بنابراین، AC=A 1 C 1، BC=B 1 C 1، ∠C=∠C 1. بنابراین، مثلث های ABC و A 1 B 1 C 1 برابر هستند
اولین معیار برای تساوی مثلث ها

قضیه ثابت می شود.

2. تقسیم یک قطعه به n قسمت مساوی.

یک پرتو را از طریق A بکشید، n بخش مساوی را روی آن قرار دهید. یک خط مستقیم از طریق B و A n و خطوط موازی با آن از طریق نقاط A 1 - A n -1 بکشید. اجازه دهید نقاط تقاطع آنها را با AB مشخص کنیم. ما n پاره ای را به دست می آوریم که طبق قضیه تالس برابر هستند.

قضیه تالس. اگر چند پاره مساوی پشت سر هم بر روی یکی از دو خط گذاشته شوند و خطوط موازی از انتهای آنها که خط دوم را قطع می کنند ترسیم کنند، آنگاه قسمت های مساوی را در خط دوم قطع می کنند.

اثبات AB=CD

1. خطوط مستقیمی را از طریق نقاط A و C موازی با طرف دیگر زاویه رسم کنید. دو متوازی الاضلاع AB 2 B 1 A 1 و CD 2 D 1 C 1 به دست می آوریم. با توجه به خاصیت متوازی الاضلاع: AB 2 = A 1 B 1 و CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 و بر اساس معیار دوم برای تساوی مثلث ها برابر هستند:
AB = CD با توجه به قضیه،
به عنوان متناظر، در تقاطع موازی BB 1 و DD 1 خط مستقیم BD تشکیل شده است.

3. به همین ترتیب، هر یک از زوایا برابر با زاویه با رأس در نقطه تلاقی دو جداره است. AB 2 = CD 2 به عنوان عناصر متناظر در مثلث های متجانس.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

پودگورنی ماکسیم

از مواد پژوهشی می توان برای باشگاه های هندسه در پایه هفتم استفاده کرد

دانلود:

پیش نمایش:

MBU DO از شهر روستوف-آن-دون "کاخ خلاقیت کودکان و جوانان"

آکادمی علوم دان برای محققان جوان به نام. یو. آ.ژدانوا

ریاضیات

موضوع: قضایای غیر استاندارد تساوی مثلث ها

پودگورنی ماکسیم، کلاس هفتم،

مدرسه متوسطه MBOU شماره 3،

سرپرست:

اولینیکوا لیودمیلا الکساندرونا،

معلم ریاضی،

مدرسه متوسطه MBOU شماره 3،

سالسک، منطقه روستوف

روستوف-آن-دون

2017

مقدمه……………………………………………………………………………………3

بخش اصلی

علائم تساوی مثلث ها…………………………………………………………………………………

نشانه‌های غیر استاندارد تساوی مثلث‌ها……………………………………………………

نتیجه گیری…………………………………………………………………………… 10

مراجع……………………………………………………………………………………………………………………………………………………………

کاربرد

معرفی.

ارتباط:

مثلث یکی از ارقام اصلی در پلان سنجی است. من از دانش آموزان دبیرستانی زیاد شنیدم که هنگام آماده شدن برای آزمون یکپارچه دولتی، اغلب باید برابری مثلث ها را ثابت کنند. و معلوم می شود که دانش علائم اساسی ناکافی است. می خواستم بدانم آیا می توان تساوی مثلث ها را با استفاده از پارامترهای دیگر اثبات کرد؟ در کتاب هندسه، که دانش آموزان مدرسه ما از آن درس می خوانند (نویسندگان L.S. Atanasyan، V.F. Butuzov، و غیره. هندسه 7-9)، تنها 3 علامت تساوی مثلث ها در نظر گرفته شده است. من بسته های آموزشی نویسندگان دیگر را بررسی کردم. اما حتی در آنها فقط سه قضیه معروف برای مطالعه ارائه شده است.

فرضیه:

آیا می توان علاوه بر سه معیار شناخته شده، معیارهای دیگری برای تساوی مثلث ها تدوین کرد؟

برای اطمینان از اینکه پاسخ این سوال نه تنها به من مربوط می شود، یک نظرسنجی جامعه شناختی در بین دانش آموزان کلاس های 7-11 انجام دادم (به پیوست 1 مراجعه کنید).

فرضیات من تایید شد. بیشتر دانش آموزان فقط سه علامت مساوی مثلث ها را می دانند.

بنابراین، هدف تحقیق من یافتن نشانه های جدیدی از برابری مثلث ها بود.

وظایف:

Θ ادبیات موضوع مورد مطالعه را مطالعه کنید.

تعداد علائم مساوی مثلث ها را مشخص کنید.

Θ وجود سایر نشانه های تساوی مثلث ها و امکان اثبات آنها را به همکلاسی ها و دانش آموزان مدرسه ما نشان دهید.

موضوع مطالعه:

بررسی علائم تساوی مثلث ها.

موضوع مطالعه. مثلث یکی از ارقام اصلی در پلان سنجی است.

روش تحقيق:نظری (مطالعه، تجزیه و تحلیل و ترکیب)، جستجوی سیستمی، عملی (اثبات قضایا).

مرجع تاریخی

مثلث یکی از چهره های مرکزی تمام هندسه است.

هنگام حل مسائل، از طیف گسترده ای از خواص آن استفاده می شود.

خواص مثلث به طور گسترده در عمل استفاده می شود: در معماری; هنگام توسعه نقشه ساختمان، هنگام برنامه ریزی آپارتمان های آینده؛ در صنعت، در طراحی قطعات مختلف، در ساخت مصالح ساختمانی، در ساخت کشتی و هواپیما. در ناوبری برای ترسیم صحیح و دقیق ترین مسیر؛ در طالع بینی و ستاره شناسی، مثلث یک رقم بسیار مهم است. مثلث ها ساختار خطوط برق فشار قوی و پل های راه آهن را قابل اعتماد می کنند.

علاوه بر این، بسیاری از مناطق دیگر وجود دارد که در آن از خواص مختلف مثلث استفاده می شود: هنگام شروع یک بازی بیلیارد، باید توپ ها را به شکل مثلث مرتب کنید، برای این کار آنها از یک دستگاه مخصوص استفاده می کنند. قرار دادن پین ها در بازی بولینگ نیز به صورت مثلث متساوی الاضلاع است. از مثلث ها برای ایجاد کف پارکت زیبا استفاده می شود. دستگاه مثلث پاسکال: هر عدد برابر است با مجموع دو عدد واقع در بالای آن (سه عدد را با یک مثلث دایره کنید). همه چیز ابتدایی است، اما چقدر معجزات در آن نهفته است! کامپیوتر مثلث پاسکال را به زبان رنگ ترجمه کرد.

موضوع مثلث را می توان به طور نامحدود ادامه داد.

مثلث های زیادی در دنیا وجود دارد!

معانی مجازی نیز از این شکل وجود دارد: به عنوان مثال، قانون "مثلث طلایی" بر اساس روانشناسی خریدار است - پس از یافتن محصول مورد نیاز خود، خریدار با عجله به صندوق پرداخت می رود. وظیفه فروشندگان این است که با قرار دادن کالاهای مورد نیاز خریدار در رأس یک مثلث خیالی، یعنی «لنگر انداختن» خریدار، او را مجبور به ماندن بیشتر در فروشگاه کنند. هر چه مساحت مثلث بزرگتر باشد، می توان طرح فروشگاه را موفق تر نامید. در یک فروشگاه مواد غذایی، این محصولات لنگر عبارتند از غذا، محصولات لبنی و نان. دیوار انتهایی قسمت فروش دومین مکان مهم است و در آنجا است که توصیه می شود محصولات لنگر را قرار دهید - دقیقاً برای اینکه خریدار مجبور شود کل محیط فروشگاه را طی کند.

مثلث معروف برمودا منطقه ای در اقیانوس اطلس است که ظاهراً ناپدید شدن مرموز کشتی ها و هواپیماها در آن رخ می دهد. این منطقه با خطوطی از فلوریدا به برمودا، به پورتوریکو و از طریق باهاما به فلوریدا محدود می شود.

بنابراین، مطالعه یک مثلث و تمام خواص آن موضوع بسیار مرتبط است.

هدف از این کار صحبت در مورد علائم تساوی مثلث ها است که یکی از مهمترین ویژگی های آنهاست.

تست های تساوی مثلث ها قضایایی هستند که بر اساس آن ها می توان ثابت کرد که برخیمثلثها برابر هستند.

در هندسه از سه علامت تساوی مثلث ها استفاده می شود.

این موضوع به طور عملی مورد مطالعه قرار گرفته است، زیرا امروزه سه معیار برای تساوی مثلث ها وجود دارد که با استفاده از قضایای مربوطه می توان آنها را اثبات کرد.

در زمان های قدیم، همراه با ستاره شناسی، علم مثلثات ظاهر شد. کلمه مثلثات از کلمه یونانی مثلث و اندازه گیری گرفته شده است. معنای لغوی آن «علم اندازه‌گیری مثلث‌ها» است.

کاهنان مصری با استفاده از طناب های کشیده به طول 3، 4 و 5 واحد هنگام ساختن معابد و غیره زوایای قائمه به دست آوردند.

هنر به تصویر کشیدن اشیا در هواپیما از زمان های قدیم توجه بشر را به خود جلب کرده است. مردم به دنبال این بودند که اطمینان حاصل کنند که تصویر به درستی شکل طبیعی جسم را منعکس می کند.

دکترین تشابه ارقام بر اساس تئوری روابط و تناسبات در یونان باستان در قرون 5-4 قبل از میلاد ایجاد شد و هنوز هم وجود دارد و توسعه می یابد. به عنوان مثال، بسیاری از اسباب بازی های کودکانه مشابه وسایل در دنیای بزرگسالان وجود دارد، کفش ها و لباس های یک سبک در اندازه های مختلف موجود است. این مثال ها را می توان ادامه داد. در نهایت، همه مردم شبیه یکدیگر هستند و همانطور که کتاب مقدس بیان می کند، خداوند آنها را به صورت و شباهت خود آفریده است.

آزمایش‌های تساوی مثلث‌ها از دیرباز اهمیت زیادی در هندسه داشته‌اند، زیرا اثبات قضایای متعدد به اثبات تساوی مثلث‌های معین کاهش یافته است. فیثاغورثی ها قبلاً درگیر اثبات علائم برابری مثلث ها بودند. به گفته پروکلوس، ائودموس رودس به تالس میلتوسی دلیلی بر تساوی دو مثلث با اضلاع مساوی و دو زاویه مجاور آن (نشان دوم برابری مثلث ها) نسبت می دهد.

تالس از این قضیه برای تعیین فاصله از ساحل تا کشتی های دریایی استفاده کرد.دقیقاً مشخص نیست که تالس از چه روشی برای این کار استفاده کرده است.

نشانه های برابری مثلث ها.

بیایید با یک تعریف شروع کنیم. مثلث های ABC و A1B1C1 در صورتی که بتوان آنها را با همپوشانی ترکیب کرد، برابر نامیده می شوند.

یک مثلث از شش عنصر تشکیل شده است: سه زاویه و سه ضلع.

این سؤال را ایجاد می کند: "کمترین تعداد عناصر مثلثی که برای ایجاد برابری دو مثلث لازم است چقدر است؟"

ما نمی توانیم بر اساس یک عنصر برابری دو مثلث را ایجاد کنیم، زیرا ناشناخته است: "آیا عناصر باقیمانده برابر خواهند بود؟"

همچنین به دلیل کمبود اطلاعات برای برقراری برابری، نمی توان با استفاده از دو عنصر برابری دو مثلث را ایجاد کرد.

می توان با استفاده از سه عنصر برابری دو مثلث را برقرار کرد. اما این سؤال را ایجاد می کند: "برای ایجاد برابری مثلث ها دقیقاً چه سه عنصر باید نامگذاری شود؟"

هنگام مطالعه این موضوع، کتاب های هندسه مدرسه نویسندگان مختلف و همچنین فرهنگ لغت ها و کتاب های مرجع را بررسی کردم. در کتاب های درسی پایه هفتم فقط سه معیار برای تساوی مثلث ها برای مطالعه پیشنهاد شده است.

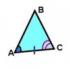
علامت Θ1 اگر دو ضلع و زاویه بین یک مثلث به ترتیب برابر با دو ضلع و زاویه بین آنها با مثلث دیگر باشد، این مثلث ها متجانس هستند.. عکس. 1

اثبات مثلث ها را در نظر بگیرید ABC و A 1 B 1 C 1 ، (شکل 1) که برای آن AB = A 1 B 1، AC = A 1 C 1 ∠ A = ∠ A 1 . اجازه دهید ثابت کنیم ΔABC = ΔA 1 B 1 C 1 .

از آنجایی که ∠A = ∠A 1 ، سپس مثلث ABC را می توان بر روی مثلث A قرار داد 1 B 1 C 1 به طوری که راس A با راس A منطبق است 1 ، و دو طرف AB و AC به ترتیب با پرتوهای A همپوشانی دارند 1 B 1 و A 1 C 1 . از آنجایی که AB = A 1 B 1، AC = A 1 C 1 ، سپس سمت AB با ضلع A تراز می شود 1 در 1 و سمت AC با ضلع A است 1 C 1 ; به طور خاص، نقاط B و B منطبق خواهند شد 1، C و C 1 . بنابراین، ضلع BC و B بر هم منطبق خواهند بود 1 C 1 . بنابراین، مثلث های ABC و A 1 B 1 C 1 کاملاً سازگار هستند، به این معنی که آنها برابر هستند.

و در اینجا نحوه استفاده از اولین علامت برابری مثلث ها در مصر باستان است (در دو ضلع و زاویه بین آنها)، تالس میلتوس نیز خالق آن برای اندازه گیری ارتفاع هرم به حساب می آید: تصور کنید که در مقابل یک هرم عظیم ایستاده ایم، چگونه می توانیم ارتفاع آن را اندازه گیری کنیم؟ از این گذشته ، شما نمی توانید ابزار اندازه گیری را به آن وصل کنید! و در اینجا اولین علامت برابری مثلث ها به کمک تالس از میلتوس می آید: او منتظر ماند تا سایه او دقیقاً با قد او منطبق شود ، قضیه را اعمال کرد ، معلوم شد که ارتفاع هرم برابر با سایه آن است (شکل 10). 2).

برنج. 2

علامت Θ2: اگر یک ضلع و دو زاویه مجاور یک مثلث به ترتیب با یک ضلع و دو زاویه مجاور یک مثلث دیگر برابر باشند، این مثلث ها متجانس هستند.

اثبات: اگر در △ABC و △A 1 B 1 C 1 برابری های زیر AB=A انجام خواهد شد 1 B 1، ∠BAC=∠B 1 A 1 C 1، ∠АВС= ∠А 1 B 1 C 1 . مثلث های A را روی هم قرار می دهیم 1 B 1 C 1 و ABC به طوری که اضلاع مساوی AB و A بر هم منطبق باشند 1 در 1 و گوشه هایی که در مجاورت آنها قرار دارند. همانطور که در مثال قبلی قبلاً مورد بحث قرار گرفت، در صورت لزوم، مثلث A 1 B 1 C 1 می‌توانید «آن را برگردانید و در طرف دیگر بگذارید». مثلث ها بر هم منطبق خواهند بود، بنابراین می توان آنها را برابر در نظر گرفت.

علامت Θ3 : اگر سه ضلع یک مثلث به ترتیب برابر با سه ضلع مثلث دیگر باشد، این مثلث ها همسو هستند. اثبات: اجازه دهید برای △ABC و △A 1 B 1 C 1 برابری های A معتبر هستند 1 B 1 =AB، B 1 C 1 = BC، C 1 A 1 = SA. مثلث A را جابه جا می کنیم 1 B 1 C 1 بنابراین آن طرف A 1 در 1 با سمت AB و راس B منطبق است 1 و B، A 1 و A منطبق می شوند. دایره ای با مرکز A و شعاع AC و دایره دومی با مرکز B و شعاع BC در نظر بگیرید. این دایره ها در دو نقطه متقارن نسبت به قطعه AB متقاطع می شوند: نقطه C و نقطه C. 2 . این بدان معنی است که C1، پس از حرکت مثلث A1B1C1، باید با هر دو نقطه C یا C2 منطبق باشد. در هر صورت، این به معنای برابری △ABC=△A خواهد بود 1 B 1 C 1 ، زیرا مثلث ها △ABC=△ABC 2 مساوی هستند (بالاخره، این مثلث ها نسبت به قطعه AB متقارن هستند.

این ویژگی - صلبیت یک مثلث - به طور گسترده در عمل استفاده می شود. بنابراین، برای محکم کردن قطب در حالت عمودی، یک تکیه گاه روی آن قرار می گیرد. هنگام نصب براکت نیز از همین اصل استفاده می شود.

خاصیت صلبیت مثلثی به طور گسترده در ساخت سازه های آهنی استفاده می شود.

از معیار سوم برای تساوی مثلث ها چنین بر می آید که مثلث یک شکل صلب است. زیرا: دو لت را می توان تصور کرد که دو سر آن با میخ بسته می شود. این طرح سفت نیست، اما با جابجایی یا بازکردن انتهای آزاد لت ها می توان زاویه بین آنها را تغییر داد. حالا یک لت دیگر برداریم و انتهای آن را با انتهای آزاد دو لت اول محکم کنیم. ساختار حاصل - یک مثلث - قبلاً سفت و سخت خواهد بود. حرکت یا جدا کردن هر دو طرف غیرممکن است، یعنی حتی یک گوشه را نمی توان تغییر داد. در واقع، اگر این امکان وجود داشت، یک مثلث جدید به دست می‌آوریم، نه برابر مثلث اصلی. اما این غیرممکن است، زیرا مثلث جدید باید برابر با مثلث اصلی در سوم باشد

در کتاب مرجع ریاضیات ابتدایی توسط M. Ya.

علامت Θ4: اگر دو ضلع و زاویه مقابل بزرگ‌تر یک مثلث به ترتیب برابر با دو ضلع و زاویه مقابل بزرگ‌تر مثلث دیگر باشند، آن‌گاه این مثلث‌ها متجانس هستند.

من این علامت را ثابت خواهم کرد.

داده شده : ΔABC، ΔA1B1C1، AB=A1B1، AC=A1C1،∠ B= ∠ B1

ثابت کنید: ΔABC=A1B1C1.

بیایید مثلث ها را مانند شکل 1 مرتب کنیم. بیایید B و B1 و سپس ΔАВВ1 را به هم وصل کنیم

متساوی الساقین یعنی∠ 1= ∠ 2. ∠ 3= ∠ 4 به عنوان باقیمانده زوایای مساوی.

ما ΔВСВ1 - متساوی الساقین را دریافت می کنیم، بنابراین ВС=В1С1. ΔАВС = ΔА1В1С1 در سه طرف.

همچنین در دوره مدرسه، 4 علامت برابری مثلث های قائم الزاویه مطرح می شود:

Θ1 . اگر پایه های یک مثلث قائم الزاویه به طور متناظر با پایه های یک مثلث دیگر برابر باشد، آنگاه این مثلث ها متجانس هستند.

Θ2 . اگر ساق و زاویه حاد مجاور یک مثلث قائم الزاویه به ترتیب برابر با ساق و زاویه حاد مجاور یک مثلث دیگر باشد، آنگاه چنین مثلث هایی همسو هستند.

Θ3 . اگر زوایای هیپوتانوس و تند یک مثلث قائم الزاویه به ترتیب برابر با زاویه هیپوتانوس و زاویه تند یک مثلث دیگر باشد، این مثلث ها همخوان هستند.

Θ4 . اگر هیپوتنوز و پایه یک مثلث قائم الزاویه به ترتیب برابر با فرضیه و پایه یک مثلث دیگر باشد، آنگاه این مثلث ها همخوان هستند.

من مبنای نظری معیارهای تساوی مثلث ها را حل کردم و اجزای دیگری را به اضلاع و زوایای مورد استفاده در آزمون های کلاسیک برای تساوی مثلث ها اضافه کردم: نیمساز، میانه و ارتفاع.

معیارهای غیر استاندارد برای همخوانی مثلث ها.

1) در دو طرف و ارتفاع کشیده شده به یکی از آنها.

داده شده: AB=A1B1، BC=B1C1، AK=A1K1،

ثابت کنید: ΔABC= ΔA1B1C1.

اثبات: ΔABK=ΔA1B1K1 توسط هیپوتنوز و پا، سپس∠ B= ∠ B1 و با توجه به علامت اول ΔABC= ΔA1B1C1 بدست آورید.

2) در دو طرف و یک وسط کشیده شده به یکی از آنها

داده شده: AB=A1B1، BC=B1C1، AK=A1K1، AK و A1K1 میانه هستند.

ثابت کنید: ΔABC= ΔA1B1C1.

اثبات:ΔABK=ΔA1B1K1 در سه طرف، یعنی∠ B= ∠ B1 و ΔABC= ΔA1B1C1 طبق علامت اول.

3) در امتداد دو طرف و ارتفاعی که از گوشه سوم کشیده شده است.

داده شده: ∠ B= ∠ B1، ∠ C= ∠ C1، AK=A1K1.

ثابت کنید: ΔABC= ΔA1B1C1.

اثبات: ΔABK=ΔA1B1K1 در امتداد ساق و زاویه حاد، یعنی BK=B1K1،

ΔACK=ΔA1C1K1 با ساق و زاویه حاد یعنی KC=K1C1 و بنابراین BC=B1C1 و ΔABC= ΔA1B1C1 با علامت دوم.

4) در امتداد یک ضلع و دو ارتفاع کشیده شده از زوایای مجاور این ضلع.

داده شده: AC=A1C1، SM=C1M1، AK=A1K1.

ثابت کنید: ΔСC= ΔA1B1C1.

اثبات: ΔAMC= ΔA1Μ1C1 در امتداد ساق و هیپوتنوز یعنی∠ A= ∠ A1 و ΔAKC= ΔA1K1C1 در امتداد ساق و هیپوتنوز یعنی∠ C= ∠ C1.

پس ΔABC= ΔA1B1C1 با توجه به معیار دوم.

5) در دو طرف و ارتفاع کشیده شده به سمت سوم.

داده شده: AB=A1B1،BC=B1C1،BK=B1K1.

ثابت کنید: ΔABC= ΔA1B1C1.

اثبات: ΔABK=ΔA1B1K1 روی هیپوتنوز و پا که به معنی AK=A1K1 است،

ΔBKC= ΔB1K1C1 در امتداد ساق و هیپوتنوز یعنی KC=K1C1.

بنابراین، ΔABC= ΔA1B1C1 در سه طرف.

6) در امتداد ضلع، یکی از زوایای مجاور این ضلع و نیمساز از این زاویه.

داده شده: AC=A1C1، AK=A1K1،∠ A ∠ A1.

ثابت کنید: ΔABC= ΔA1B1C1.

برهان: ΔКАС=ΔК1А1С1 طبق علامت اول یعنی∠ C= ∠ C1،

ΔABC= ΔA1B1C1 با توجه به مشخصه دوم.

7) با دو ارتفاع و زاویه ای که یکی از ارتفاعات از آن کشیده شده است.

داده شده: SM=S1M1، AK=A1K1، ∠ A ∠ A1.

ثابت کنید: ΔABC= ΔA1B1C1.

اثبات: ΔAMC= ΔA1Μ1C1 روی ساق و زاویه حاد، ΔКАС=ΔK1A1С1 روی ساق و هیپوتنوز، ΔABC= ΔA1B1C1 در علامت دوم.

نتیجه.

در حین تحقیق متوجه شدم که علاوه بر سه علامت اصلی تساوی مثلث ها، می توان بسیاری دیگر را نیز نشان داد. من تساوی مثلث ها را بر اساس میانه، ارتفاع، نیمساز مثلث در ترکیب با اضلاع و زوایای مثلث، با رعایت حضور سه عنصر، فرموله و اثبات کردم. اکنون می توانم به دانش آموزان مدرسه خود بگویم که علائم دیگری نیز وجود دارد که مثلث ها برابر هستند. این به فارغ التحصیلان مدرسه این امکان را می دهد تا نتایج تحقیقات من را در آمادگی برای آزمون یکپارچه دولتی و آزمون یکپارچه دولتی به کار گیرند و با استفاده از این ویژگی ها به راحتی مسائل هندسی را حل کنند.

نتیجه تحقیقات من: معیارهای متعددی برای تساوی مثلث هایی که در درس هندسه مدرسه مورد مطالعه قرار نمی گیرند، اثبات شده است.

کتابشناسی - فهرست کتب

1. ویگودسکی ام.یا. کتاب راهنمای ریاضیات ابتدایی.
2. هندسه. پایه های 7-9: کتاب درسی. برای آموزش عمومی مؤسسات/L.S.Atanasyan، V.F.Butuzov، S.B. Kadomtsev و همکاران - ویرایش 19. - م.: آموزش و پرورش، 2009.
3. Pogorelov A.V. هندسه: کتاب درسی. برای پایه های 7-9. آموزش عمومی نهادها. – ویرایش سوم. - م.: آموزش و پرورش، 2002.
4. . دایره المعارف "آوانتا" در ریاضیات، مسکو، 2004.
5. 2. ویکی پدیا یک دانشنامه آزاد است.
6. 3. گلیزر جی.آی. "تاریخ ریاضیات در مدرسه"، مسکو، Prosveshchenie، 1982.
7. 4. گوسوا تی.ام. نشانه های شباهت مثلث ها - مسکو، اول سپتامبر، مکمل "ریاضیات"، 1999، شماره 28
8. 5. Pogorelov A.V. "هندسه پایه های 7-9"مسکو، آموزش و پرورش، 2003

پیوست 1

1. به نظر شما چند علامت مساوی مثلث است؟

الف) 3 ب) بیش از سه ج) کمتر از سه

2. آیا دوست دارید علائم جدیدی برای همخوانی مثلث ها یاد بگیرید؟

الف) بله ب) خیر

اگر بتوان دو مثلث را از طریق همپوشانی به هم نزدیک کرد، گفته می شود که همخوان هستند. شکل 1 مثلث های مساوی ABC و A 1 B 1 C 1 را نشان می دهد. هر یک از این مثلث ها را می توان بر روی دیگری قرار داد تا کاملاً با هم سازگار باشند، یعنی راس و اضلاع آنها به صورت جفت با هم مطابقت داشته باشند. واضح است که زوایای این مثلث ها نیز به صورت جفت با هم مطابقت خواهند داشت.

بنابراین، اگر دو مثلث متجانس باشند، عناصر (یعنی اضلاع و زوایای) یک مثلث به ترتیب برابر با عناصر مثلث دیگر هستند. توجه داشته باشید که در مثلث های مساوی در برابر اضلاع مشابه(به عنوان مثال، وقتی روی هم قرار می گیرند) زوایای مساوی دروغ می گویدو برگشت: اضلاع مساوی به ترتیب در مقابل زوایای مساوی قرار دارند.

بنابراین، به عنوان مثال، در مثلث های مساوی ABC و A 1 B 1 C 1 که در شکل 1 نشان داده شده است، به ترتیب در مقابل اضلاع مساوی AB و A 1 B 1، زوایای C و C 1 مساوی قرار دارند. برابری مثلث های ABC و A 1 B 1 C 1 را به صورت زیر نشان می دهیم: Δ ABC = Δ A 1 B 1 C 1. معلوم می شود که با مقایسه برخی از عناصر آنها می توان تساوی دو مثلث را تعیین کرد.

قضیه 1. اولین علامت تساوی مثلث ها.اگر دو ضلع و زاویه بین آنها از یک مثلث به ترتیب برابر با دو ضلع و زاویه بین آنها با مثلث دیگر باشد، در این صورت چنین مثلث هایی متجانس هستند (شکل 2).

اثبات مثلث های ABC و A 1 B 1 C 1 را در نظر بگیرید که در آنها AB = A 1 B 1، AC = A 1 C 1 ∠ A = ∠ A 1 (نگاه کنید به شکل 2). اجازه دهید ثابت کنیم که Δ ABC = Δ A 1 B 1 C 1 .

از آنجایی که ∠ A = ∠ A 1، پس مثلث ABC را می توان روی مثلث A 1 B 1 C 1 قرار داد تا راس A با راس A 1 تراز شود و اضلاع AB و AC به ترتیب بر روی پرتوهای A 1 B 1 و A 1 قرار گیرند. ج 1 . از آنجایی که AB = A 1 B 1، AC = A 1 C 1، پس سمت AB با ضلع A 1 B 1 و ضلع AC با ضلع A 1 C 1 تراز خواهد شد. به طور خاص، نقاط B و B 1، C و C 1 منطبق خواهند شد. در نتیجه، اضلاع BC و B 1 C 1 بر هم منطبق خواهند بود. بنابراین، مثلث های ABC و A 1 B 1 C 1 کاملاً سازگار هستند، یعنی با هم برابر هستند.

قضیه 2 به روشی مشابه با استفاده از روش برهم نهی ثابت می شود.

قضیه 2. دومین علامت تساوی مثلث ها.اگر یک ضلع و دو زاویه مجاور یک مثلث به ترتیب با ضلع و دو زاویه مجاور یک مثلث دیگر برابر باشند، آنگاه چنین مثلث هایی همسو هستند (شکل 34).

اظهار نظر. بر اساس قضیه 2، قضیه 3 ایجاد می شود.

قضیه 3. مجموع هر دو زاویه داخلی مثلث کمتر از 180 درجه است.

قضیه 4 از قضیه آخر پیروی می کند.

قضیه 4. زاویه بیرونی یک مثلث بزرگتر از هر زاویه داخلی است که مجاور آن نباشد.

قضیه 5. سومین علامت تساوی مثلث ها.اگر سه ضلع یک مثلث به ترتیب برابر با سه ضلع مثلث دیگر باشد، آنگاه این مثلث ها متجانس هستند ().

مثال 1.در مثلث های ABC و DEF (شکل 4)

∠ A = ∠ E، AB = 20 سانتی متر، AC = 18 سانتی متر، DE = 18 سانتی متر، EF = 20 سانتی متر مثلث های ABC و DEF را با هم مقایسه کنید. چه زاویه ای در مثلث DEF برابر با زاویه B است؟

راه حل. این مثلث ها با توجه به علامت اول برابر هستند. زاویه F مثلث DEF برابر با زاویه B مثلث ABC است، زیرا این زاویه ها به ترتیب در مقابل اضلاع مساوی DE و AC قرار دارند.

مثال 2.بخش های AB و CD (شکل 5) در نقطه O که وسط هر یک از آنها است، قطع می شوند. اگر قطعه AC 6 متر باشد، طول قطعه BD چقدر است؟

راه حل. مثلث های AOC و BOD برابر هستند (طبق معیار اول): ∠ AOC = ∠ BOD (عمودی)، AO = OB، CO = OD (بر اساس شرط).
از تساوی این مثلث ها به دست می آید که اضلاع آنها برابر است، یعنی AC = BD. اما از آنجایی که طبق شرط AC = 6 m، پس BD = 6 m.