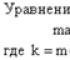Praca praktyczna nr 2

„Funkcja różnicowa”

Cel lekcji: Naucz się rozwiązywać przykłady i problemy na ten temat.

Pytania teoretyczne (bazowe):

1. Zastosowanie pochodnych do badania funkcji ekstremalnych.

2. Różniczka funkcji, jej znaczenie geometryczne i fizyczne.

3. Różniczka zupełna funkcji kilku zmiennych.

4. Stan organizmu jako funkcja wielu zmiennych.

5. Przybliżone obliczenia.

6. Znajdowanie pochodnych cząstkowych i różnic całkowitych.

7. Przykłady zastosowania tych pojęć w farmakokinetyce, mikrobiologii itp.

(samodzielne przygotowanie)

1. odpowiadać na pytania dotyczące tematu lekcji;

2. rozwiązywać przykłady.

Przykłady

Znajdź różniczki następujących funkcji:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

Stosowanie pochodnych do badania funkcji

Warunek na to, aby funkcja y = f(x) wzrastała na przedziale [a, b]

Warunek na to, aby funkcja y=f(x) malała na odcinku [a, b]

Warunek maksymalnej funkcji y=f(x)przy x=a

f"(a)=0 i f"" (a)<0

Jeżeli przy x=a pochodne f”(a) = 0 i f”(a) = 0, to należy zbadać f”(x) w sąsiedztwie punktu x = a. Funkcja y=f( x) przy x=a ma maksimum , jeżeli przy przejściu przez punkt x = a pochodna f"(x) zmienia znak z "+" na "-", w przypadku minimum - z "-" do „+” Jeśli f”(x) nie zmienia znaku przy przejściu przez punkt x = a, to w tym punkcie funkcja nie ma ekstremum

Funkcja różnicowa.

Różniczka zmiennej niezależnej jest równa jej przyrostowi:

Różniczka funkcji y=f(x)

Różniczka sumy (różnicy) dwóch funkcji y=u±v

Różniczka iloczynu dwóch funkcji y=uv

Różniczka ilorazu dwóch funkcji y=u/v

dy=(vdu-udv)/v 2

Przyrost funkcji

Δy = f(x + Δx) - f(x) ≈ dy ≈ f"(x) Δx

gdzie Δx: - przyrost argumentu.

Przybliżone obliczenie wartości funkcji:

f(x + Δx) ≈ f(x) + f"(x) Δx

Zastosowanie różniczki w obliczeniach przybliżonych

Różnicę stosuje się do obliczania błędów bezwzględnych i względnych w pomiarach pośrednich u = f(x, y, z.). Błąd bezwzględny wyniku pomiaru

du≈Δu≈|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…

Błąd względny wyniku pomiaru

du/u≈Δu/u≈(|du/dx|Δx+|du/dy|Δy+|du/dz|Δz+…)/u

FUNKCJA RÓŻNICOWA.

Różniczka funkcji jako główna część przyrostu funkcji I.Ściśle powiązane z pojęciem pochodnej jest pojęcie różniczki funkcji. Niech funkcja k(x) jest ciągła dla danych wartości X i ma pochodną

D f/Dx = f¢(x) + a(Dx), skąd przyrost funkcji Df = f¢(x)Dx + a(Dx)Dx, Gdzie a(Dx)® 0 Na Dх® 0. Ustalmy rząd nieskończenie małego f¢(x)Dx Dx.:

Dlatego nieskończenie małe f¢(x)Dx I Dx mają ten sam rząd małości, tj f¢(x)Dx = O.

Ustalmy rząd nieskończenie małego a(Dх)Dх w stosunku do nieskończenie małego Dx:

Dlatego nieskończenie małe a(Dх)Dх ma wyższy rząd małości w porównaniu z nieskończenie małym Dx, to jest a(Dx)Dx = o.

Zatem nieskończenie mały przyrost Df funkcję różniczkowalną można przedstawić w postaci dwóch wyrazów: nieskończenie f¢(x)Dx tego samego rzędu małości z Dx i nieskończenie małe a(Dх)Dх wyższy rząd małości w porównaniu z nieskończenie małym Dx. Oznacza to, że w równości Df=f¢(x)Dx + a(Dx)Dx Na Dx® 0 to znaczy drugi człon ma tendencję do zera „szybciej” niż pierwszy a(Dx)Dx = o.

Pierwszy warunek f¢(x)Dx, liniowy względem Dx, zwany funkcja różniczkowa k(x) w tym punkcie X i oznaczać dy Lub zm(czytaj „de igrek” lub „de ef”). Więc,

dy = df = f¢(x)Dx.

Analityczne znaczenie różniczki polega na tym, że różniczka funkcji jest główną częścią przyrostu funkcji Df, liniowy względem przyrostu argumentu Dx. Różniczka funkcji różni się od przyrostu funkcji o nieskończenie małą wartość wyższego rzędu małości niż Dx. Naprawdę, Df=f¢(x)Dx + a(Dx)Dx Lub Df = df + a(Dx)Dx . Różnica argumentów dx równy jego przyrostowi Dx: dx=Dx.

Przykład. Oblicz wartość różnicową funkcji f(x) = x 3 + 2x, Gdy X waha się od 1 do 1,1.

Rozwiązanie. Znajdźmy ogólne wyrażenie na różniczkę tej funkcji:

Podstawianie wartości dx=Dx=1,1–1= 0,1 I x = 1 do ostatniego wzoru otrzymujemy pożądaną wartość różnicy: zm½ x=1; = 0,5.

CZĘŚCIOWE INSTRUMENTY POCHODNE I RÓŻNICOWE.

Pochodne cząstkowe pierwszego rzędu. Pochodna cząstkowa pierwszego rzędu funkcji z = f(x,y ) argumentacją X w danym punkcie (x;y) zwany limitem

jeśli istnieje.

Pochodna cząstkowa funkcji z = f(x, y) argumentacją X jest oznaczony jednym z następujących symboli:

Podobnie pochodna cząstkowa względem Na oznaczane i definiowane wzorem:

Ponieważ pochodna cząstkowa jest pochodną zwyczajną funkcji jednego argumentu, nie jest trudno ją obliczyć. Aby to zrobić, należy zastosować wszystkie omówione dotychczas zasady różniczkowania, biorąc pod uwagę w każdym przypadku, który z argumentów jest traktowany jako „liczba stała”, a który służy jako „zmienna różniczkująca”.

Komentarz. Aby znaleźć pochodną cząstkową, na przykład, w odniesieniu do argumentu x – df/dx, wystarczy znaleźć pochodną zwyczajną funkcji f(x,y), uznając to drugie za funkcję jednego argumentu X, A Na– stała; znaleźć df/dy- nawzajem.

Przykład. Znajdź wartości pochodnych cząstkowych funkcji f(x,y) = 2x 2 + y2 w tym punkcie P(1;2).

Rozwiązanie. Rachunkowość f(x, y) funkcja jednego argumentu X i korzystając z zasad różniczkowania, znajdujemy

W punkcie P(1;2) wartość pochodna

Biorąc pod uwagę f(x;y) jako funkcję jednego argumentu y, znajdujemy

W punkcie P(1;2) wartość pochodna

ZADANIE DO SAMODZIELNEJ PRACY STUDENTA:

Znajdź różniczki następujących funkcji:

Rozwiąż następujące problemy:

1. O ile zmniejszy się pole kwadratu o boku x=10 cm, jeżeli bok zmniejszymy o 0,01 cm?

2. Podano równanie ruchu ciała: y=t 3 /2+2t 2, gdzie s wyraża się w metrach, t w sekundach. Znajdź drogę s przebytą przez ciało w t=1,92 s od początku ruchu.

LITERATURA

1. Lobotskaya N.L. Podstawy matematyki wyższej - M.: „Szkoła Wyższa”, 1978.C198-226.

2. Bailey N. Matematyka w biologii i medycynie. Za. z angielskiego M.: „Mir”, 1970.

3. Remizov A.N., Isakova N.Kh., Maksina L.G. Zbiór zagadnień fizyki medycznej i biologicznej - M.: „Szkoła Wyższa”, 1987. P16-20.

Pochodne cząstkowe funkcji dwóch zmiennych.
Koncepcja i przykłady rozwiązań

W tej lekcji będziemy kontynuować naszą znajomość funkcji dwóch zmiennych i rozważymy być może najczęstsze zadanie tematyczne - znalezienie pochodne cząstkowe pierwszego i drugiego rzędu oraz całkowita różniczka funkcji. Studenci studiów niestacjonarnych z reguły spotykają się z pochodnymi cząstkowymi na pierwszym roku, w drugim semestrze. Co więcej, z moich obserwacji wynika, że ​​na egzaminie prawie zawsze pojawia się zadanie znalezienia pochodnych cząstkowych.

Aby efektywnie przestudiować poniższy materiał, ty niezbędny potrafić z mniejszą lub większą pewnością znaleźć „zwykłe” pochodne funkcji jednej zmiennej. Na lekcjach możesz dowiedzieć się, jak prawidłowo obchodzić się z instrumentami pochodnymi Jak znaleźć pochodną? I Pochodna funkcji zespolonej. Przyda nam się też tabela pochodnych funkcji elementarnych i reguł różniczkowania, najwygodniej, jeśli jest pod ręką w formie drukowanej. Materiały referencyjne można znaleźć na stronie Wzory i tablice matematyczne.

Powtórzmy na szybko koncepcję funkcji dwóch zmiennych, postaram się ograniczyć do absolutnego minimum. Funkcja dwóch zmiennych jest zwykle zapisywana jako , przy czym zmienne są wywoływane niezależne zmienne Lub argumenty.

Przykład: – funkcja dwóch zmiennych.

Czasami używa się notacji. Istnieją również zadania, w których zamiast litery używana jest litera.

Z geometrycznego punktu widzenia funkcja dwóch zmiennych reprezentuje najczęściej powierzchnię w przestrzeni trójwymiarowej (płaszczyzna, walec, kula, paraboloida, hiperboloida itp.). Ale tak naprawdę jest to bardziej geometria analityczna, a naszym planem jest analiza matematyczna, której mój nauczyciel akademicki nigdy nie pozwolił mi spisać na straty i która jest moją „mocną stroną”.

Przejdźmy do kwestii znalezienia pochodnych cząstkowych pierwszego i drugiego rzędu. Dla tych, którzy wypili już kilka kaw i szykują się do słuchania niesamowicie trudnego materiału, mam dobrą wiadomość: pochodne cząstkowe to prawie to samo, co „zwykłe” pochodne funkcji jednej zmiennej.

W przypadku pochodnych cząstkowych obowiązują wszystkie reguły różniczkowania i tablica pochodnych funkcji elementarnych. Jest tylko kilka drobnych różnic, które zaraz poznamy:

...tak przy okazji tego tematu, który założyłem mała książeczka w formacie PDF, który pozwoli Ci „wbić zęby” w zaledwie kilka godzin. Ale korzystając z witryny, z pewnością uzyskasz ten sam wynik - może tylko trochę wolniej:

Przykład 1

Znajdź pochodne cząstkowe funkcji pierwszego i drugiego rzędu

Najpierw znajdźmy pochodne cząstkowe pierwszego rzędu. Jest ich dwóch.

Oznaczenia:
lub – pochodna cząstkowa względem „x”
lub – pochodna cząstkowa względem „y”

Zacznijmy . Kiedy znajdziemy pochodną cząstkową względem „x”, zmienną uważa się za stałą (stała liczba).

Komentarze do wykonanych działań:

(1) Pierwszą rzeczą, którą robimy, szukając pochodnej cząstkowej, jest wniosek Wszystko funkcja w nawiasie pod liczbą pierwszą z indeksem.

Uwaga, ważne! NIE TRACIMY indeksów dolnych podczas procesu rozwiązywania. W takim przypadku, jeśli narysujesz gdzieś „obrys” bez , nauczyciel może przynajmniej umieścić go obok zadania (natychmiast odgryź część punktu za nieuwagę).

(2) Stosujemy reguły różniczkowania , . W takim prostym przykładzie obie reguły można łatwo zastosować w jednym kroku. Zwróć uwagę na pierwsze określenie: od uważa się za stałą, a każdą stałą można usunąć ze znaku pochodnej, następnie usuwamy to z nawiasów. Oznacza to, że w tej sytuacji nie jest lepszy niż zwykła liczba. Spójrzmy teraz na trzeci termin: wręcz przeciwnie, nie ma tu nic do wyciągnięcia. Skoro jest stałą, to też jest stałą i w tym sensie nie jest lepsza od ostatniego członu – „siedem”.

(3) Używamy tabelarycznych instrumentów pochodnych i .

(4) Uprośćmy lub, jak lubię mówić, „poprawmy” odpowiedź.

Teraz . Kiedy znajdziemy pochodną cząstkową względem „y”, to zmiennauważany za stały (stała liczba).

(1) Stosujemy te same zasady różnicowania , . W pierwszym członie usuwamy stałą ze znaku pochodnej, w drugim członie nie możemy nic wyjąć, ponieważ jest to już stała.

(2) Korzystamy z tabeli pochodnych funkcji elementarnych. Zamieńmy w myślach wszystkie „X” w tabeli na „I”. Oznacza to, że ta tabela jest równie ważna dla (a właściwie dla prawie każdej litery). W szczególności formuły, których używamy, wyglądają następująco: i .

Jakie jest znaczenie pochodnych cząstkowych?

W istocie pochodne cząstkowe pierwszego rzędu przypominają „zwykła” pochodna:

- Ten Funkcje, które charakteryzują tempo zmian działa odpowiednio w kierunku osi i . A więc na przykład funkcja charakteryzuje stromość „wzniesień” i „zboczy” powierzchnie w kierunku osi odciętych, a funkcja mówi nam o „reliefie” tej samej powierzchni w kierunku osi rzędnych.

! Notatka : tutaj mamy na myśli wskazówki, które równoległy osie współrzędnych.

Dla lepszego zrozumienia rozważmy konkretny punkt na płaszczyźnie i obliczmy w nim wartość funkcji („wysokość”):
– a teraz wyobraź sobie, że jesteś tutaj (NA POWIERZCHNI).

Obliczmy pochodną cząstkową względem „x” w danym punkcie:

O tym mówi nam znak ujemny pochodnej „X”. malejące działa w punkcie w kierunku osi odciętej. Innymi słowy, jeśli zrobimy mały, mały (nieskończenie mały) krok w kierunku końca osi (równolegle do tej osi), następnie zejdziemy w dół po zboczu powierzchni.

Teraz dowiadujemy się o naturze „terenu” w kierunku osi rzędnych:

Pochodna po „y” jest dodatnia, zatem w punkcie w kierunku osi funkcja wzrasta. Krótko mówiąc, czeka nas podjazd pod górę.

Ponadto charakteryzuje się pochodną cząstkową w punkcie tempo zmian działa w odpowiednim kierunku. Im większa uzyskana wartość modulo– im bardziej stroma powierzchnia i odwrotnie, im jest ona bliższa zeru, tym powierzchnia jest bardziej płaska. Zatem w naszym przykładzie „nachylenie” w kierunku osi odciętych jest bardziej strome niż „góra” w kierunku osi rzędnych.

Ale to były dwie prywatne ścieżki. Jest całkiem jasne, że od momentu, w którym się znajdujemy, (i ogólnie z dowolnego punktu na danej powierzchni) możemy pójść w innym kierunku. Istnieje zatem zainteresowanie stworzeniem ogólnej „mapy nawigacyjnej”, która informowałaby nas o „krajobrazie” powierzchni Jeśli to możliwe w każdym punkcie dziedzina definicji tej funkcji wszystkimi dostępnymi ścieżkami. O tym i innych ciekawych rzeczach opowiem na jednej z kolejnych lekcji, ale na razie wróćmy do technicznej strony zagadnienia.

Usystematyzujmy elementarne stosowane zasady:

1) Kiedy różniczkujemy względem , zmienną uważa się za stałą.

2) Gdy różnicowanie przeprowadza się wg, wówczas jest uważany za stały.

3) Reguły i tabela pochodnych funkcji elementarnych obowiązują i mają zastosowanie do dowolnej zmiennej (lub dowolnej innej), według której przeprowadza się różniczkowanie.

Krok drugi. Znajdujemy pochodne cząstkowe drugiego rzędu. Jest ich czterech.

Oznaczenia:
lub – druga pochodna względem „x”
lub – druga pochodna względem „y”
Lub - mieszany pochodna „x według igr”
Lub - mieszany pochodna „Y”

Z drugą pochodną nie ma problemów. W prostych słowach, druga pochodna jest pochodną pierwszej pochodnej.

Dla wygody przepiszę znalezione już pochodne cząstkowe pierwszego rzędu:

Najpierw znajdźmy pochodne mieszane:

Jak widać wszystko jest proste: bierzemy pochodną cząstkową i różniczkujemy ją jeszcze raz, ale w tym przypadku - tym razem po „Y”.

Podobnie:

W praktycznych przykładach możesz skupić się na następującej równości:

Zatem za pomocą pochodnych mieszanych drugiego rzędu bardzo wygodnie jest sprawdzić, czy poprawnie znaleźliśmy pochodne cząstkowe pierwszego rzędu.

Znajdź drugą pochodną względem „x”.
Żadnych wynalazków, weźmy to i różniczkuj go ponownie przez „x”:

Podobnie:

Należy zauważyć, że przy znalezieniu musisz pokazać zwiększona uwaga, gdyż nie ma cudownych równości, które by je zweryfikowały.

Szerokie zastosowanie praktyczne znajdują także drugie pochodne, w szczególności wykorzystywane są w problematyce znajdowania ekstrema funkcji dwóch zmiennych. Ale wszystko ma swój czas:

Przykład 2

Oblicz pochodne cząstkowe funkcji pierwszego rzędu w tym punkcie. Znajdź pochodne drugiego rzędu.

To jest przykład, który możesz rozwiązać samodzielnie (odpowiedzi na końcu lekcji). Jeśli masz trudności z rozróżnieniem korzeni, wróć do lekcji Jak znaleźć pochodną? Ogólnie rzecz biorąc, już wkrótce nauczysz się znajdować takie instrumenty pochodne „w locie”.

Przejdźmy lepiej do bardziej złożonych przykładów:

Przykład 3

Sprawdź to . Zapisz różnicę całkowitą pierwszego rzędu.

Rozwiązanie: Znajdź pochodne cząstkowe pierwszego rzędu:

Zwróć uwagę na indeks dolny: , obok „X” nie wolno pisać w nawiasach, że jest to stała. Ta uwaga może być bardzo przydatna dla początkujących, aby ułatwić nawigację po rozwiązaniu.

Dalsze komentarze:

(1) Wszystkie stałe przesuwamy poza znak pochodnej. W tym przypadku i , i dlatego ich iloczyn jest uważany za liczbę stałą.

(2) Nie zapomnij, jak prawidłowo różnicować korzenie.

(1) Wszystkie stałe usuwamy ze znaku pochodnej; w tym przypadku stała wynosi .

(2) Pod liczbą pierwszą pozostał nam iloczyn dwóch funkcji, dlatego musimy skorzystać z reguły różniczkowania iloczynu .

(3) Nie zapominaj, że jest to funkcja złożona (aczkolwiek najprostsza ze złożonych). Używamy odpowiedniej reguły: .

Teraz znajdujemy mieszane pochodne drugiego rzędu:

Oznacza to, że wszystkie obliczenia zostały wykonane poprawnie.

Zapiszmy całkowitą różnicę. W kontekście rozważanego zadania nie ma sensu mówić, jaka jest całkowita różniczka funkcji dwóch zmiennych. Ważne jest, aby tę różnicę bardzo często trzeba było zapisać w praktycznych zadaniach.

Całkowita różnica pierwszego rzędu funkcja dwóch zmiennych ma postać:

W tym przypadku:

Oznacza to, że wystarczy głupio zastąpić już znalezione pochodne cząstkowe pierwszego rzędu we wzorze. W tej i podobnych sytuacjach najlepiej zapisać w licznikach znaki różniczkowe:

Zgodnie z wielokrotnymi prośbami czytelników, Pełny mechanizm różnicowy drugiego rzędu.

To wygląda tak:

UWAŻNIE znajdźmy „jednoliterowe” pochodne drugiego rzędu:

i zapisz „potwora”, ostrożnie „łącząc” kwadraty, iloczyn i nie zapominając o podwojeniu mieszanej pochodnej:

Nie ma problemu, jeśli coś wydaje się trudne, do instrumentów pochodnych zawsze możesz wrócić później, gdy opanujesz technikę różniczkowania:

Przykład 4

Znajdź pochodne cząstkowe funkcji pierwszego rzędu . Sprawdź to . Zapisz różnicę całkowitą pierwszego rzędu.

Spójrzmy na serię przykładów ze złożonymi funkcjami:

Przykład 5

Znajdź pochodne cząstkowe funkcji pierwszego rzędu.

Rozwiązanie:

Przykład 6

Znajdź pochodne cząstkowe funkcji pierwszego rzędu .
Zapisz całkowitą różnicę.

To jest przykład, który możesz rozwiązać samodzielnie (odpowiedź na końcu lekcji). Nie podam pełnego rozwiązania, bo jest dość proste.

Dość często wszystkie powyższe zasady są stosowane w połączeniu.

Przykład 7

Znajdź pochodne cząstkowe funkcji pierwszego rzędu .

(1) Korzystamy z reguły różniczkowania sumy

(2) Pierwszy termin w tym przypadku jest uważany za stały, ponieważ w wyrażeniu nie ma nic zależnego od „x” - tylko „y”. Wiesz, zawsze miło jest, gdy ułamek można zamienić na zero). Dla drugiego członu stosujemy zasadę różnicowania produktów. Swoją drogą w tym sensie nic by się nie zmieniło, gdyby zamiast tego podano funkcję – ważne, że tutaj iloczyn dwóch funkcji, KAŻDY z nich zależy od "X", dlatego należy zastosować regułę różnicowania produktów. Dla trzeciego członu stosujemy zasadę różniczkowania funkcji zespolonej.

(1) Pierwszy wyraz zarówno w liczniku, jak i mianowniku zawiera „Y”, dlatego należy zastosować regułę różniczkowania ilorazów: . Drugi wyraz zależy TYLKO od „x”, co oznacza, że ​​jest uważany za stałą i zwraca się do zera. W przypadku trzeciego członu stosujemy regułę różniczkowania funkcji zespolonej.

Tym czytelnikom, którzy odważnie dotarli prawie do końca lekcji, opowiem na uspokojenie stary dowcip Mechmatowa:

Któregoś dnia w przestrzeni funkcji pojawiła się zła pochodna i zaczęła różnicować wszystkich. Wszystkie funkcje są rozproszone we wszystkich kierunkach, nikt nie chce się przekształcać! I tylko jedna funkcja nie ucieka. Pochodna podchodzi do niej i pyta:

- Dlaczego ode mnie nie uciekniesz?

- Ha. Ale nie obchodzi mnie to, bo jestem „e do potęgi X”, a ty mi nic nie zrobisz!

Na co zły pochodny z podstępnym uśmiechem odpowiada:

- Tu się mylisz, odróżnię cię przez „Y”, więc powinieneś być zerem.

Kto zrozumiał żart, opanował już derywaty przynajmniej do poziomu „C”).

Przykład 8

Znajdź pochodne cząstkowe funkcji pierwszego rzędu .

To jest przykład, który możesz rozwiązać samodzielnie. Pełne rozwiązanie i przykład problemu znajdują się na końcu lekcji.

Cóż, to prawie wszystko. Na koniec nie mogę nie zadowolić miłośników matematyki jeszcze jednym przykładem. Tu nawet nie chodzi o amatorów, każdy ma inny poziom przygotowania matematycznego – są osoby (i nie takie rzadkie), które lubią rywalizować z trudniejszymi zadaniami. Chociaż ostatni przykład w tej lekcji nie jest tak skomplikowany, jak uciążliwy z obliczeniowego punktu widzenia.

Aby uprościć rejestrację i prezentację materiału, ograniczymy się do przypadku funkcji dwóch zmiennych. Wszystko, co następuje, dotyczy również funkcji dowolnej liczby zmiennych.

Definicja. Pochodna częściowa Funkcje z = f(x, y) według zmiennej niezależnej X zwany pochodną

obliczone przy stałej Na.

W podobny sposób wyznacza się pochodną cząstkową po zmiennej Na.

W przypadku pochodnych cząstkowych obowiązują zwykłe zasady i wzory na różniczkowanie.

Definicja. Iloczyn pochodnej cząstkowej i przyrost argumentu X(y) nazywa się częściowy mechanizm różnicowy według zmiennej X(Na) funkcje dwóch zmiennych z = f(x, y) (symbol: ):

Jeśli pod różnicą zmiennej niezależnej dx(dy) zrozumieć przyrost X(Na), To

Dla funkcji z = f(x, y) znajdźmy geometryczne znaczenie jego pochodnych częstotliwości i .

Rozważ kwestię, punkt P 0 (X 0 ,y 0 , z 0) na powierzchni z = f(X,Na) i krzywa L, który uzyskuje się poprzez przecięcie powierzchni płaszczyzną y = y 0. Krzywą tę można postrzegać jako wykres funkcji jednej zmiennej z = f(x, y) w samolocie y = y 0. Jeśli jest trzymany w punkcie R 0 (X 0 , j 0 , z 0) styczna do krzywej L, to zgodnie z geometrycznym znaczeniem pochodnej funkcji jednej zmiennej , Gdzie A – kąt utworzony przez styczną z dodatnim kierunkiem osi Oh.

Lub: W podobny sposób ustalmy inną zmienną, tj. przekrójmy powierzchnię z = f(x, y) samolot x = x 0. Następnie funkcja

z = f(X 0 , j) można uznać za funkcję jednej zmiennej Na:

Gdzie B– kąt utworzony przez styczną w punkcie M 0 (X 0 , j 0) z dodatnim kierunkiem osi Oj(ryc. 1.2).

Ryż. 1.2. Ilustracja geometrycznego znaczenia pochodnych cząstkowych

Przykład 1.6. Biorąc pod uwagę funkcję z = x 2 – 3xy – 4Na 2 – x + 2ty + 1. Znajdź i .

Rozwiązanie. Rozważając Na jako stałą, otrzymujemy

Rachunkowość X stałe, stwierdzamy

Wykład 3 FNP, pochodne cząstkowe, różniczka

Jaka jest najważniejsza rzecz, której nauczyliśmy się na ostatnim wykładzie?

Dowiedzieliśmy się, jaka jest funkcja kilku zmiennych, posługując się argumentem z przestrzeni euklidesowej. Zbadaliśmy, czym jest granica i ciągłość takiej funkcji

Czego dowiemy się na tym wykładzie?

Kontynuując nasze badania FNP, będziemy badać pochodne cząstkowe i różniczki tych funkcji. Nauczmy się, jak zapisać równanie płaszczyzny stycznej i normalnej do powierzchni.

Pochodna cząstkowa, różniczka zupełna FNP. Związek różniczkowalności funkcji z istnieniem pochodnych cząstkowych

Dla funkcji jednej zmiennej rzeczywistej, po przestudiowaniu tematów „Granice” i „Ciągłość” (Wprowadzenie do rachunku różniczkowego), zbadano pochodne i różniczki tej funkcji. Przejdźmy do rozważenia podobnych pytań dla funkcji kilku zmiennych. Należy zauważyć, że jeśli wszystkie argumenty oprócz jednego są ustalone w FNP, wówczas FNP generuje funkcję jednego argumentu, dla której można uwzględnić przyrost, różnicę i pochodną. Nazwiemy je odpowiednio przyrostem częściowym, różniczką cząstkową i pochodną cząstkową. Przejdźmy do precyzyjnych definicji.

Definicja 10. Niech będzie podana funkcja zmiennych gdzie - element przestrzeni euklidesowej i odpowiadające mu przyrosty argumentów , ,…, . Gdy wartości nazywane są częściowymi przyrostami funkcji. Całkowity przyrost funkcji jest ilością.

Na przykład dla funkcji dwóch zmiennych, gdzie jest to punkt na płaszczyźnie i , odpowiadające przyrosty argumentów, przyrosty częściowe będą wynosić , . W tym przypadku wartością jest całkowity przyrost funkcji dwóch zmiennych.

Definicja 11. Pochodna cząstkowa funkcji zmiennych nad zmienną to granica stosunku częściowego przyrostu funkcji nad tą zmienną do przyrostu odpowiedniego argumentu, gdy dąży on do 0.

Zapiszmy definicję 11 jako wzór lub w formie rozszerzonej. (2) Dla funkcji dwóch zmiennych Definicja 11 będzie zapisana w postaci wzorów , . Z praktycznego punktu widzenia definicja ta oznacza, że ​​przy obliczaniu pochodnej cząstkowej względem jednej zmiennej wszystkie pozostałe zmienne są stałe i tę funkcję rozważamy jako funkcję jednej wybranej zmiennej. Pochodną zwyczajną oblicza się względem tej zmiennej.

Przykład 4. Dla funkcji gdzie znajdź pochodne cząstkowe i punkt, w którym obie pochodne cząstkowe są równe 0.

Rozwiązanie . Obliczmy pochodne cząstkowe, i zapisz system w postaci Rozwiązaniem tego układu są dwa punkty i .

Zastanówmy się teraz, w jaki sposób koncepcja dyferencjału jest uogólniana na FNP. Przypomnijmy, że funkcję jednej zmiennej nazywa się różniczkowalną, jeśli jej przyrost jest przedstawiony w postaci , w tym przypadku ilość jest główną częścią przyrostu funkcji i nazywa się jej różniczką. Ilość jest funkcją , ma tę właściwość, że jest funkcją nieskończenie małą w porównaniu do . Funkcja jednej zmiennej jest różniczkowalna w punkcie wtedy i tylko wtedy, gdy ma w tym punkcie pochodną. W tym przypadku stała i jest równa tej pochodnej, tj. wzór obowiązuje dla różnicy .

Jeśli weźmiemy pod uwagę częściowy przyrost FNP, to zmienia się tylko jeden z argumentów i ten częściowy przyrost można uznać za przyrost funkcji jednej zmiennej, czyli sprawdza się ta sama teoria. Zatem warunek różniczkowalności zachodzi wtedy i tylko wtedy, gdy istnieje pochodna cząstkowa, w którym to przypadku różniczka cząstkowa jest dana przez .

Jaka jest całkowita różnica funkcji kilku zmiennych?

Definicja 12. Funkcja zmiennej w pewnym punkcie nazywany różniczkowalnym , jeśli jego przyrost jest przedstawiony w postaci . W tym przypadku główna część przyrostu nazywana jest różnicą FNP.

Zatem różniczką FNP jest wartość. Wyjaśnijmy, co rozumiemy pod pojęciem ilości , które nazwiemy nieskończenie małym w porównaniu do przyrostów argumentów . Jest to funkcja, która ma tę właściwość, że jeśli wszystkie przyrosty oprócz jednego są równe 0, to równość jest prawdziwa . Zasadniczo oznacza to, że = = + +…+ .

Jak powiązane są ze sobą warunki różniczkowalności FNP i warunki istnienia pochodnych cząstkowych tej funkcji?

Twierdzenie 1. Jeśli funkcja zmiennych jest różniczkowalna w punkcie , to ma pochodne cząstkowe względem wszystkich zmiennych w tym punkcie i w tym samym czasie.

Dowód. Równość piszemy dla i w formie i podziel obie strony powstałej równości przez . W otrzymanej równości przechodzimy do granicy w . W rezultacie otrzymujemy wymaganą równość. Twierdzenie zostało udowodnione.

Konsekwencja. Różnicę funkcji zmiennych oblicza się ze wzoru . (3)

W przykładzie 4 różniczka funkcji była równa . Zauważ, że ta sama różnica w punkcie jest równa . Ale jeśli obliczymy to w punkcie z przyrostami , wówczas różnica będzie równa . Zauważ, że , dokładna wartość danej funkcji w punkcie jest równa , ale ta sama wartość, w przybliżeniu obliczona przy użyciu pierwszej różnicy, jest równa . Widzimy, że zastępując przyrost funkcji różniczką, możemy w przybliżeniu obliczyć wartości funkcji.

Czy funkcja kilku zmiennych będzie różniczkowalna w punkcie, jeśli ma w tym punkcie pochodne cząstkowe? W przeciwieństwie do funkcji jednej zmiennej, odpowiedź na to pytanie jest negatywna. Dokładne sformułowanie zależności podaje następujące twierdzenie.

Twierdzenie 2. Jeśli funkcja zmiennych w punkcie istnieją ciągłe pochodne cząstkowe względem wszystkich zmiennych, to funkcja jest w tym punkcie różniczkowalna.

Jak . W każdym nawiasie zmienia się tylko jedna zmienna, więc w obu przypadkach możemy zastosować wzór na przyrost skończony Lagrange'a. Istota tego wzoru polega na tym, że dla ciągle różniczkowalnej funkcji jednej zmiennej różnica między wartościami funkcji w dwóch punktach jest równa wartości pochodnej w pewnym punkcie pośrednim, pomnożonej przez odległość między punktami. Stosując tę ​​formułę do każdego z nawiasów, otrzymujemy . Ze względu na ciągłość pochodnych cząstkowych, pochodna w punkcie i pochodna w punkcie różnią się od pochodnych w punkcie wielkościami i , dążąc do 0 jako , dążąc do 0. Ale wtedy oczywiście . Twierdzenie zostało udowodnione. i współrzędna. Sprawdź, czy ten punkt należy do powierzchni. Zapisz równanie płaszczyzny stycznej i równanie normalnej do powierzchni we wskazanym punkcie.

Rozwiązanie. Naprawdę, . Na ostatnim wykładzie obliczyliśmy już różniczkę tej funkcji w dowolnym punkcie, w danym punkcie jest ona równa . W konsekwencji równanie płaszczyzny stycznej zostanie zapisane w postaci lub , a równanie normalnej - w postaci .

Każda pochodna cząstkowa (wg X i przez y) funkcji dwóch zmiennych jest pochodną zwyczajną funkcji jednej zmiennej dla ustalonej wartości drugiej zmiennej:

(Gdzie y= stała),

(Gdzie X= stała).

Dlatego pochodne cząstkowe oblicza się za pomocą wzory i zasady obliczania pochodnych funkcji jednej zmiennej, biorąc pod uwagę stałą innej zmiennej.

Jeśli nie potrzebujesz analizy przykładów i wymaganego do tego minimum teorii, a jedynie rozwiązania swojego problemu, to przejdź do kalkulator pochodnej cząstkowej online .

Jeśli ciężko jest się skoncentrować, aby śledzić, gdzie w funkcji znajduje się stała, to w projekcie rozwiązania przykładu zamiast zmiennej o ustalonej wartości można podstawić dowolną liczbę - wtedy można szybko obliczyć pochodną cząstkową jako zwykła pochodna funkcji jednej zmiennej. Trzeba tylko pamiętać o zwróceniu stałej (zmiennej o ustalonej wartości) na jej miejsce po zakończeniu ostatecznego projektu.

Opisana powyżej właściwość pochodnych cząstkowych wynika z definicji pochodnej cząstkowej, która może pojawić się w pytaniach egzaminacyjnych. Dlatego też, aby zapoznać się z poniższą definicją, można otworzyć odnośnik teoretyczny.

Pojęcie ciągłości funkcji z= F(X, y) w punkcie definiuje się podobnie do tego pojęcia dla funkcji jednej zmiennej.

Funkcjonować z = F(X, y) nazywa się ciągłym w punkcie jeśli

Różnicę (2) nazywa się całkowitym przyrostem funkcji z(uzyskuje się go w wyniku przyrostów obu argumentów).

Niech będzie podana funkcja z= F(X, y) i kropka

Jeśli funkcja się zmieni z występuje, gdy zmienia się tylko jeden z argumentów, np. X, ze stałą wartością innego argumentu y, wówczas funkcja otrzyma przyrost

zwany częściowym przyrostem funkcji F(X, y) Przez X.

Rozważam zmianę funkcji z w zależności od zmiany tylko jednego z argumentów, efektywnie przechodzimy na funkcję jednej zmiennej.

Jeśli istnieje skończona granica

wówczas nazywa się to pochodną cząstkową funkcji F(X, y) za pomocą argumentu X i jest oznaczony jednym z symboli

(4)

W podobny sposób określa się przyrost częściowy z Przez y:

i pochodna cząstkowa F(X, y) Przez y:

(6)

Przykład 1.

Rozwiązanie. Znajdujemy pochodną cząstkową względem zmiennej „x”:

(y naprawił);

Znajdujemy pochodną cząstkową względem zmiennej „y”:

(X naprawił).

Jak widać nie ma znaczenia w jakim stopniu zmienna jest stała: w tym przypadku po prostu pewna liczba jest czynnikiem (jak w przypadku pochodnej zwykłej) zmiennej, z którą znajdziemy pochodną cząstkową . Jeśli zmienna stała nie zostanie pomnożona przez zmienną, z którą znajdziemy pochodną cząstkową, to ta samotna stała, niezależnie od tego, w jakim stopniu, jak w przypadku pochodnej zwykłej, zniknie.

Przykład 2. Biorąc pod uwagę funkcję

Znajdź pochodne cząstkowe

(przez X) i (przez Y) i obliczyć ich wartości w punkcie A (1; 2).

Rozwiązanie. Na stałe y pochodną pierwszego wyrazu wyznaczamy jako pochodną funkcji potęgowej ( tabela funkcji pochodnych jednej zmiennej):

.

Na stałe X pochodną pierwszego wyrazu wyznaczamy jako pochodną funkcji wykładniczej, a drugiego - jako pochodną stałej:

Obliczmy teraz wartości tych pochodnych cząstkowych w punkcie A (1; 2):

Rozwiązanie problemów z pochodnymi cząstkowymi możesz sprawdzić na stronie kalkulator pochodnej cząstkowej online .

Przykład 3. Znajdź pochodne cząstkowe funkcji

Rozwiązanie. W jednym kroku znajdziemy

(y X, tak jakby argumentem sinusa było 5 X: analogicznie przed znakiem funkcji pojawia się 5);

(X jest stała i w tym przypadku jest mnożnikiem przy y).

Rozwiązanie problemów z pochodnymi cząstkowymi możesz sprawdzić na stronie kalkulator pochodnej cząstkowej online .

W podobny sposób definiuje się pochodne cząstkowe funkcji trzech lub więcej zmiennych.

Jeśli każdy zestaw wartości ( X; y; ...; T) zmienne niezależne ze zbioru D odpowiada jednej konkretnej wartości ty od wielu mi, To ty nazywana funkcją zmiennych X, y, ..., T i oznaczać ty= F(X, y, ..., T).

Dla funkcji trzech lub więcej zmiennych nie ma interpretacji geometrycznej.

Wyznacza się i oblicza także pochodne cząstkowe funkcji kilku zmiennych przy założeniu, że zmienia się tylko jedna ze zmiennych niezależnych, a pozostałe są stałe.

Przykład 4. Znajdź pochodne cząstkowe funkcji

.

Rozwiązanie. y I z naprawił:

X I z naprawił:

X I y naprawił:

Znajdź samodzielnie pochodne cząstkowe, a następnie spójrz na rozwiązania

Przykład 5.

Przykład 6. Znajdź pochodne cząstkowe funkcji.

Pochodna cząstkowa funkcji kilku zmiennych ma to samo znaczenie mechaniczne jest takie samo jak pochodna funkcji jednej zmiennej, jest szybkością zmian funkcji względem zmiany jednego z argumentów.

Przykład 8. Ilościowa wartość przepływu P pasażerów kolei można wyrazić funkcją

Gdzie P- Liczba pasażerów, N– liczba mieszkańców punktów korespondencyjnych, R– odległość pomiędzy punktami.

Pochodna cząstkowa funkcji P Przez R, równy

pokazuje, że spadek potoku pasażerów jest odwrotnie proporcjonalny do kwadratu odległości pomiędzy odpowiednimi punktami o tej samej liczbie mieszkańców w punktach.

Pochodna częściowa P Przez N, równy

pokazuje, że wzrost potoku pasażerskiego jest proporcjonalny do dwukrotnej liczby mieszkańców miejscowości położonych w tej samej odległości między punktami.

Rozwiązanie problemów z pochodnymi cząstkowymi możesz sprawdzić na stronie kalkulator pochodnej cząstkowej online .

Pełny mechanizm różnicowy

Iloczyn pochodnej cząstkowej i przyrostu odpowiedniej zmiennej niezależnej nazywa się różniczką cząstkową. Różnice częściowe oznacza się następująco:

Suma różnic cząstkowych wszystkich zmiennych niezależnych daje różnicę całkowitą. Dla funkcji dwóch zmiennych niezależnych całkowitą różnicę wyraża się przez równość

(7)

Przykład 9. Znajdź całkowitą różnicę funkcji

Rozwiązanie. Wynik zastosowania wzoru (7):

Funkcję, która ma różnicę całkowitą w każdym punkcie pewnej dziedziny, nazywamy różniczkowalną w tej dziedzinie.

Znajdź samodzielnie różnicę całkowitą, a następnie spójrz na rozwiązanie

Podobnie jak w przypadku funkcji jednej zmiennej, różniczkowalność funkcji w pewnej dziedzinie implikuje jej ciągłość w tej dziedzinie, ale nie odwrotnie.

Sformułujmy bez dowodu warunek wystarczający na różniczkowalność funkcji.

Twierdzenie. Jeśli funkcja z= F(X, y) ma ciągłe pochodne cząstkowe

w danym obszarze, to jest on różniczkowalny w tym obszarze i jego różniczkę wyraża się wzorem (7).

Można wykazać, że podobnie jak w przypadku funkcji jednej zmiennej, różniczką funkcji jest główna liniowa część przyrostu funkcji, tak w przypadku funkcji kilku zmiennych, różnica całkowita wynosi główna, liniowa względem przyrostów zmiennych niezależnych, część całkowitego przyrostu funkcji.

Dla funkcji dwóch zmiennych całkowity przyrost funkcji ma postać

(8)

gdzie α i β są nieskończenie małe w i .

Pochodne cząstkowe wyższego rzędu

Pochodne cząstkowe i funkcje F(X, y) same w sobie są pewnymi funkcjami tych samych zmiennych i z kolei mogą mieć pochodne względem różnych zmiennych, które nazywane są pochodnymi cząstkowymi wyższych rzędów.