»Lekcja 12. Ranga macierzy. Obliczanie rangi macierzy. Norma macierzowa

Lekcja numer 12. Ranga macierzy. Obliczanie rangi macierzy. Norma macierzy.

Jeśli wszyscy nieletni w matrycyAzamówienieksą równe zero, to wszystkie mniejsze rzędu k+1, jeśli takie istnieją, również są równe zeru.
Według rangi macierzy A jest największym z rzędów nieletnich matrycy A niezerowe.
Maksymalna ranga może być równa minimalnej liczbie wierszy lub kolumn macierzy, tj. jeśli macierz to 4x5, to maksymalna ranga wyniesie 4.
Minimalna ranga macierzy to 1, chyba że mamy do czynienia z macierzą zerową, gdzie ranga zawsze wynosi zero.

Rząd niezdegenerowanej macierzy kwadratowej rzędu n jest równy n, ponieważ jej wyznacznikiem jest podrzędna rzędu n, a macierz niezdegenerowana jest niezerowa.
Gdy macierz jest transponowana, jej ranga się nie zmienia.

Niech rząd macierzy będzie. Następnie nazywa się każdy mniejszy rzędu niezerowego podstawowa drobna.
Przykład. Dana macierz A.

Wyznacznikiem macierzy jest zero.
Nieletni drugiego rzędu ... Dlatego r (A) = 2 i podstawowy małoletni.
Bazowy minor to także minor .
Mniejszy odkąd = 0, więc nie będzie podstawowe.
Ćwiczenie: samodzielnie sprawdź, które inne nieletnie dzieci drugiego rzędu będą podstawowe, a które nie.

Znalezienie rangi macierzy poprzez obliczenie wszystkich jej podrzędnych wymaga zbyt wiele pracy obliczeniowej. (Czytelnik może sprawdzić, czy w macierzy kwadratowej czwartego rzędu jest 36 drugorzędnych drugorzędnych.) Dlatego do znalezienia rangi używany jest inny algorytm. Do jej opisania wymagany jest szereg dodatkowych informacji.

Nazwijmy następujące działania na macierzach przekształceniami elementarnymi macierzy:
1) permutacja wierszy lub kolumn;
2) pomnożenie wiersza lub kolumny przez liczbę inną niż zero;
3) dodanie do jednego z wierszy kolejnego wiersza pomnożonego przez liczbę lub dodanie do jednej z kolumn innej kolumny pomnożonej przez liczbę.

Przekształcenia elementarne nie zmieniają rangi macierzy.
Algorytm obliczania rangi macierzy jest podobny do algorytmu obliczania wyznacznika i polega na tym, że za pomocą przekształceń elementarnych macierz sprowadza się do prostej postaci, dla której znalezienie rangi nie jest trudne. Ponieważ ranga nie zmieniała się przy każdej transformacji, obliczając rangę przekształconej macierzy, w ten sposób znajdujemy rangę macierzy oryginalnej.

Niech będzie wymagane obliczenie rangi macierzy rozmiarów mxn.

W wyniku obliczeń macierz A1 ma postać

Jeśli wszystkie wiersze zaczynające się od trzeciego mają wartość zero, to od nieletnich ... W przeciwnym razie, przestawiając wiersze i kolumny z liczbami większymi niż dwa, uzyskujemy, że trzeci element trzeciego wiersza jest niezerowy. Ponadto, dodając trzeci wiersz, pomnożony przez odpowiednie liczby, do wierszy z dużymi liczbami, otrzymujemy zera w trzeciej kolumnie, zaczynając od czwartego elementu, i tak dalej.
Na pewnym etapie dochodzimy do macierzy, w której wszystkie wiersze, zaczynając od (r+1), są równe zeru (lub ich nie ma), a mała w pierwszych wierszach i pierwszych kolumnach jest wyznacznikiem macierz trójkątna z niezerowymi elementami na przekątnej... Ranga takiej macierzy to. Dlatego Rang (A) = r.

W proponowanym algorytmie wyznaczania rangi macierzy wszystkie obliczenia należy wykonywać bez zaokrąglania. Dowolna niewielka zmiana przynajmniej jednego z elementów macierzy pośrednich może spowodować, że otrzymana odpowiedź będzie różniła się od rangi macierzy pierwotnej o kilka jednostek.
Jeśli elementy w oryginalnej macierzy były liczbami całkowitymi, wygodnie jest wykonywać obliczenia bez użycia ułamków. Dlatego na każdym etapie wskazane jest mnożenie ciągów przez liczby tak, aby w obliczeniach nie pojawiały się ułamki.

W praktycznej pracy laboratoryjnej rozważ przykład znajdowania rzędu macierzy.

ALGORYTM LOKALIZACJI STANDARDY MATRYCOWE .
Istnieją tylko trzy normy matrycowe.
Pierwsza norma macierzy= maksymalna liczba otrzymana przez dodanie wszystkich elementów każdej kolumny, wzięta modulo.
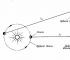
Przykład: niech będzie dana macierz A 3x2 (rys. 10). Pierwsza kolumna zawiera elementy: 8, 3, 8. Wszystkie elementy są dodatnie. Znajdźmy ich sumę: 8 + 3 + 8 = 19. Druga kolumna zawiera elementy: 8, -2, -8. Dwa elementy są ujemne, dlatego przy dodawaniu tych liczb należy podstawić moduł tych liczb (czyli bez znaków „minus”). Znajdźmy ich sumę: 8 + 2 + 8 = 18. Maksymalna z tych dwóch liczb to 19. Czyli pierwsza norma macierzy to 19.

Rysunek 10.

Druga norma macierzy jest pierwiastkiem kwadratowym z sumy kwadratów wszystkich elementów macierzy. A to oznacza, że ​​podwajamy wszystkie elementy macierzy, a następnie dodajemy otrzymane wartości i wyciągamy pierwiastek kwadratowy z wyniku.
W naszym przypadku norma 2 macierzy jest równa pierwiastkowi kwadratowemu z 269. Na diagramie z grubsza wyciągnąłem pierwiastek kwadratowy z 269 iw rezultacie otrzymałem około 16,401. Chociaż bardziej poprawne jest nie wyodrębnianie korzenia.

Trzecia norma macierzy to maksymalna liczba otrzymana przez dodanie wszystkich elementów każdego wiersza, wzięta modulo.
W naszym przykładzie: pierwsza linia zawiera elementy: 8, 8. Wszystkie elementy są dodatnie. Znajdźmy ich sumę: 8 + 8 = 16. Drugi wiersz zawiera elementy: 3, -2. Jeden z elementów jest ujemny, dlatego dodając te liczby, należy podstawić moduł tej liczby. Znajdźmy ich sumę: 3 + 2 = 5. Trzecia linia zawiera elementy 8 i -8. Jeden z elementów jest ujemny, dlatego dodając te liczby, należy podstawić moduł tej liczby. Znajdźmy ich sumę: 8 + 8 = 16. Maksymalna z tych trzech liczb to 16. Czyli trzecia norma macierzy to 16.

Opracował: Saliy N.A.

Kolegium YouTube

1 / 1

✪ Norma wektorowa. Część 4.

Napisy na filmie obcojęzycznym

Definicja

Niech K będzie polem podłoża (zwykle K = r lub K = C ) i jest przestrzenią liniową wszystkich macierzy o m rzędach i n kolumnach, składających się z elementów K. Na przestrzeni macierzy podaje się normę, jeśli każda macierz jest powiązana z nieujemną liczbą rzeczywistą ‖ A ‖ (\ styl wyświetlania \ | A \ |), nazwał swoją normą, więc

W przypadku macierzy kwadratowych (tj. m = n), macierze można mnożyć bez opuszczania przestrzeni, a zatem normy w tych przestrzeniach zwykle spełniają również właściwość submultiplikatywność :

Submultiplikatywność można również wykonać dla norm macierzy niekwadratowych, ale zdefiniować dla kilku wymaganych rozmiarów jednocześnie. Mianowicie, jeśli A jest macierzą ℓ  ×  m, a B to macierz m ×  n, następnie B- macierz ℓ  ×  n .

Normy operatora

Ważną klasą norm macierzowych są normy operatora, określany również jako podwładni lub wywołany ... Norma operatora jest jednoznacznie skonstruowana zgodnie z dwiema normami określonymi w i, wychodząc z faktu, że dowolna macierz m ×  n jest reprezentowana przez operator liniowy z K n (\ styl wyświetlania K ^ (n)) v K m (\ styl wyświetlania K ^ (m))... Konkretnie,

‖ A ‖ = sup (‖ A x ‖: x ∈ K n, ‖ x ‖ = 1) = sup (‖ A x ‖ ‖ x ‖: x ∈ K n, x ≠ 0). (\ displaystyle (\ początek (wyrównany) \ | A \ | & = \ sup \ (\ | Ax \ |: x \ in K ^ (n), \ \ | x \ | = 1 \) \\ & = \ sup \ left \ ((\ frac (\ | Ax \ |) (\ | x \ |)): x \ in K ^ (n), \ x \ neq 0 \ right \). \ end (wyrównane)))

Pod warunkiem spójnej specyfikacji norm na przestrzeniach wektorowych, taka norma jest submultiplikatywna (patrz).

Przykłady norm operatorskich

Właściwości normy spektralnej:

1. Norma widmowa operatora jest równa maksymalnej liczbie pojedynczej tego operatora.
2. Norma widmowa normalnego operatora jest równa wartości bezwzględnej maksymalnej wartości własnej modulo tego operatora.
3. Norma spektralna nie zmienia się, gdy macierz jest mnożona przez macierz ortogonalną (jednostkową).

Normy macierzy niebędące operatorami

Istnieją normy macierzowe, które nie są normami operatora. Pojęcie nieoperatorskich norm macierzy zostało wprowadzone przez Yu.I. Lyubicha, a zbadane przez G.R.Belitskiego.

Przykład normy nieoperatorskiej

Rozważmy na przykład dwie różne normy operatora ‖ A ‖ 1 (\ styl wyświetlania \ | A \ | _ (1)) oraz ‖ A ‖ 2 (\ styl wyświetlania \ | A \ | _ (2)), takie jak normy wierszy i kolumn. Formowanie nowej normy ‖ A ‖ = m a x (‖ A ‖ 1, ‖ A ‖ 2) (\ displaystyle \ | A \ | = max (\ | A \ | _ (1), \ | A \ | _ (2)))... Nowa norma ma właściwość pierścienia ‖ A B ‖ ≤ ‖ A ‖ ‖ B ‖ (\ displaystyle \ | AB \ | \ leq \ | A \ | \ | B \ |), zachowuje jedność ‖ I ‖ = 1 (\ styl wyświetlania \ | I \ | = 1) i nie jest operatorem.

Przykłady norm

Wektor p (\ styl wyświetlania p)-norma

Może być brany pod uwagę m × n (\ styl wyświetlania m \ razy n) macierz jako wektor wielkości m n (\ styl wyświetlania mn) i użyj standardowych norm wektorowych:

‖ A ‖ p = ‖ vec (A) ‖ p = (∑ i = 1 m ∑ j = 1 n | aij | p) 1 / p (\ displaystyle \ | A \ | _ (p) = \ | \ mathrm ( vec) (A) \ | _ (p) = \ lewo (\ suma _ (i = 1) ^ (m) \ suma _ (j = 1) ^ (n) | a_ (ij) | ^ (p) \ prawo) ^ (1 / p))

Norma Frobeniusa

Norma Frobeniusa, lub norma euklidesowa jest szczególnym przypadkiem normy p dla P = 2 : ‖ A ‖ F = ∑ i = 1 m ∑ j = 1 naij 2 (\ displaystyle \ | A \ | _ (F) = (\ sqrt (\ sum _ (i = 1) ^ (m) \ sum _ (j = 1) ^ (n) a_ (ij) ^ (2)))).

Norma Frobeniusa jest łatwa do obliczenia (w porównaniu np. z normą widmową). Posiada następujące właściwości:

‖ A x ‖ 2 2 = ∑ i = 1 m | ∑ j = 1 n a i j x j | 2 ≤ ∑ i = 1 m (∑ j = 1 n | a i j | 2 ∑ j = 1 n | x j | 2) = ∑ j = 1 n | xj | 2 ‖ A ‖ F 2 = ‖ A ‖ F 2 ‖ x ‖ 2 2. (\ displaystyle \ | Ax \ | _ (2) ^ (2) = \ suma _ (i = 1) ^ (m) \ left | \ suma _ (j = 1) ^ (n) a_ (ij) x_ ( j) \ right | ^ (2) \ leq \ sum _ (i = 1) ^ (m) \ left (\ sum _ (j = 1) ^ (n) | a_ (ij) | ^ (2) \ sum _ (j = 1) ^ (n) | x_ (j) | ^ (2) \ prawo) = \ suma _ (j = 1) ^ (n) | x_ (j) | ^ (2) \ | A \ | _ (F) ^ (2) = \ | A \ | _ (F) ^ (2) \ | x \ | _ (2) ^ (2).)

• Submultiplikatywność: ‖ A B ‖ F ≤ ‖ A ‖ F ‖ B ‖ F (\ displaystyle \ | AB \ | _ (F) \ leq \ | A \ | _ (F) \ | B \ | _ (F)), ponieważ ‖ A B ‖ F 2 = ∑ i, j | ∑ k a i k b k j | 2 ≤ ∑ i, j (∑ k | a i k | | b k j |) 2 ≤ ∑ i, j (∑ k | a i k | 2 ∑ k | b k j | 2) = ∑ i, k | a ja k | 2 ∑ k, j | bkj | 2 = ‖ A ‖ F 2 ‖ B ‖ F 2 (\ displaystyle \ | AB \ | _ (F) ^ (2) = \ suma _ (i, j) \ left | \ suma _ (k) a_ (ik) b_ (kj) \ prawo | ^ (2) \ leq \ suma _ (i, j) \ lewo (\ sum _ (k) | a_ (ik) || b_ (kj) | \ prawo) ^ (2) \ leq \ sum _ (i, j) \ lewo (\ sum _ (k) | a_ (ik) | ^ (2) \ sum _ (k) | b_ (kj) | ^ (2) \ prawo) = \ suma _ (i, k) | a_ (ik) | ^ (2) \ suma _ (k, j) | b_ (kj) | ^ (2) = \ | A \ | _ (F) ^ (2) \ | B \ | _ (F) ^ (2)).
• ‖ A ‖ F 2 = tr ⁡ A ∗ A = tr ⁡ AA ∗ (\ displaystyle \ | A \ | _ (F) ^ (2) = \ mathop (\ rm (tr)) A ^ (*) A = \ mathop (\ rm (tr)) AA ^ (*)), gdzie t r ⁡ A (\ styl wyświetlania \ mathop (\ rm (tr)) A)- ślad macierzy A (\ styl wyświetlania A), A ∗ (\ styl wyświetlania A ^ (*)) jest sprzężoną macierzą hermitowską.
• ‖ A ‖ F 2 = ρ 1 2 + ρ 2 2 + ⋯ + ρ n 2 (\ displaystyle \ | A \ | _ (F) ^ (2) = \ rho _ (1) ^ (2) + \ rho _ (2) ^ (2) + \ kropki + \ rho _ (n) ^ (2)), gdzie ρ 1, ρ 2,…, ρ n (\ styl wyświetlania \ rho _ (1), \ rho _ (2), \ kropki, \ rho _ (n))- wartości osobliwe matrycy A (\ styl wyświetlania A).
• ‖ A ‖ F (\ styl wyświetlania \ | A \ | _ (F)) nie zmienia się przy mnożeniu macierzy A (\ styl wyświetlania A) lewo lub prawo do macierzy ortogonalnych (jednostkowych).

Maksimum modułu

Maksymalna norma modułu jest kolejnym szczególnym przypadkiem normy p dla P = ∞ .

‖ A ‖ max = max (| a i j |). (\ displaystyle \ | A \ | _ (\ text (max)) = \ max \ (| a_ (ij) | \).)

Norma Schattena

Spójność norm macierzy i wektorów

Norma macierzowa ‖ ⋅ ‖ a b (\ styl wyświetlania \ | \ cdot \ | _ (ab)) na K m × n (\ styl wyświetlania K ^ (m \ razy n)) nazywa Zgoda z normami ‖ ⋅ ‖ a (\ styl wyświetlania \ | \ cdot \ | _ (a)) na K n (\ styl wyświetlania K ^ (n)) oraz ‖ ⋅ ‖ b (\ styl wyświetlania \ | \ cdot \ | _ (b)) na K m (\ styl wyświetlania K ^ (m)), Jeśli:

‖ A x ‖ b ≤ ‖ A ‖ a b ‖ x ‖ a (\ displaystyle \ | Ax \ | _ (b) \ leq \ | A \ | _ (ab) \ | x \ | _ (a))

dla każdego A ∈ K m × n, x ∈ K n (\ displaystyle A \ in K ^ (m \ razy n), x \ in K ^ (n))... Konstrukcja normy operatora jest zgodna z pierwotną normą wektorów.

Przykłady uzgodnionych, ale nie podporządkowanych norm macierzowych:

Równoważność norm

Wszystkie normy w kosmosie K m × n (\ styl wyświetlania K ^ (m \ razy n)) są równoważne, czyli dla dowolnych dwóch norm . ‖ Α (\ styl wyświetlania \ |. \ | _ (\ Alpha)) oraz . ‖ Β (\ styl wyświetlania \ |. \ | _ (\ Beta)) i dla dowolnej matrycy A ∈ K m × n (\ styl wyświetlania A \ w K ^ (m \ razy n)) podwójna nierówność jest prawdziwa.

Norma macierzowa nazwiemy liczbę rzeczywistą przypisaną do tej macierzy || A || takiej, która jako liczba rzeczywista jest przypisana do każdej macierzy z przestrzeni n-wymiarowej i spełnia 4 aksjomaty:

1. ||A ||³0 i ||A ||=0 tylko wtedy, gdy A jest macierzą zerową;

2. ||αA ||=|α|·||A ||, gdzie a R;

3. || A + B || £ || A || + || B ||;

4. || A · ​​​​B || £ || A || · || B ||. (właściwość multiplikatywna)

Normę matryc można wprowadzać na różne sposoby. Macierz A może być postrzegana jako n 2 - wektor wymiarowy.

Ta norma nazywana jest normą euklidesową macierzy.

Jeżeli dla dowolnej macierzy kwadratowej A i dowolnego wektora x, którego wymiar jest równy rządowi macierzy, nierówność || Ax || £ || A || · || x ||

wtedy mówi się, że norma macierzy A jest zgodna z normą wektora. Zauważ, że po lewej stronie ostatniego warunku znajduje się norma wektora (Ax jest wektorem).

Z daną normą wektorową skoordynowane są różne normy macierzowe. Wybierzmy z nich najmniejszą. To będzie

Ta norma macierzowa jest podporządkowana danej normie wektorowej. Istnienie maksimum w tym wyrażeniu wynika z ciągłości normy, ponieważ zawsze istnieje wektor x -> ||x ||=1 i ||Ax ||=||A ||.

Pokażmy, że norma N (A) nie podlega żadnej normie wektorowej. Normy macierzy, z zastrzeżeniem wcześniej wprowadzonych norm wektorowych, wyrażają się następująco:

1. ||A || ¥ = | a ij | (norma-maksimum)

2. ||A || 1 = |aij | (suma-norma)

3. ||A || 2 =, (norma widmowa)

gdzie s 1 jest największą właściwą wartością macierzy symetrycznej A ¢ A, będącej iloczynem macierzy transponowanych i macierzy pierwotnych. T k macierz A ¢ A jest symetryczna, to wszystkie jej wartości własne są rzeczywiste i dodatnie. Liczba l -własności jest wartością, a niezerowy wektor x jest wektorem własnym macierzy A (jeśli są powiązane relacją Ax = lx). Jeśli sama macierz A jest symetryczna, A ¢ = A, to A ¢ A = A 2, a następnie s 1 =, gdzie jest największą wartością własną modułu macierzy A. Zatem w tym przypadku mamy =.

Wartości własne macierzy nie przekraczają żadnej z jej uzgodnionych norm. Normalizując relację definiującą wartości własne, otrzymujemy || λx || = || Ax ||, | λ | · || x || = || Ax || £ || A || · || x ||, | λ | £ || A ||

Od || A || 2 zł || A || e, gdzie norma euklidesowa jest łatwa do obliczenia, w oszacowaniach zamiast normy spektralnej można zastosować normę euklidesową macierzy.

30. Warunkowość układów równań. Współczynnik warunku .

Warunkowość- wpływ decyzji na dane wyjściowe. Topór = b: wektor b odpowiada decyzji x... Zostawiać b zmieni się według wartości. Następnie wektor b + nowe rozwiązanie będzie pasować x + : A (x + ) = b +... Ponieważ system jest liniowy, to Topór + A = b +, następnie A = ; = ; = ; b = Topór; = wtedy; *, gdzie jest względnym błędem perturbacji rozwiązania, - czynnik warunkuwarunki (A) (ile razy błąd rozwiązania może wzrosnąć), jest względnym zaburzeniem wektora b. warunki (A) = ; przew (A) * Właściwości współczynnika: zależy od wyboru normy matrycowej; warunki ( = przew (A); pomnożenie macierzy przez liczbę nie wpływa na współczynnik warunku. Im większy współczynnik, tym większy błąd w danych początkowych wpływa na rozwiązanie SLAE. Numer warunku nie może być mniejszy niż 1.

31. Metoda przemiatania rozwiązywania układów liniowych równań algebraicznych.

Często konieczne jest rozwiązywanie układów, których macierze są słabo wypełnione, tj. zawierające wiele niezerowych elementów. Macierze takich systemów mają zwykle określoną strukturę, wśród których są systemy z macierzami o strukturze paskowej, tj. w nich niezerowe elementy znajdują się na głównej przekątnej i na kilku przekątnych bocznych. W przypadku rozwiązywania systemów z macierzami paskowymi metodę Gaussa można przekształcić w bardziej wydajne metody. Rozważmy najprostszy przypadek układów pasmowych, do których, jak zobaczymy później, sprowadza się rozwiązanie problemów dyskretyzacji dla zagadnień brzegowych dla równań różniczkowych metodami różnic skończonych, elementów skończonych itp. sąsiadujące z nim:

Trzy macierze diagonalne mają tylko (3n-2) niezerowe wpisy.

Zmieńmy nazwy współczynników macierzy:

Wówczas w notacji składowej układ można przedstawić jako:

A i * x i-1 + b i * x i + c i * x i + 1 = d i , i = 1, 2, ..., n; (7)

a 1 = 0, c n = 0. (osiem)

Struktura systemu zakłada związek tylko między sąsiednimi niewiadomymi:

x ja = x ja * x ja +1 + h ja (9)

x i -1 = x i -1 * x i + h i -1 i podstaw w (7):

A i (x i-1 * x i + h i-1) + b i * x i + c i * x i + 1 = d i

(a i * x i-1 + b i) x i = –c i * x i + 1 + d i –a i * h i-1

Porównując otrzymane wyrażenie z reprezentacją (7), otrzymujemy:

Wzory (10) reprezentują relacje powtarzalności do obliczania współczynników przemiatania. Wymagają ustawienia początkowych wartości. Zgodnie z pierwszym warunkiem (8) dla i = 1 mamy a 1 = 0, a zatem

Ponadto pozostałe współczynniki przemiatania są obliczane i przechowywane według wzorów (10) dla i = 2,3, ..., n, a dla i = n, biorąc pod uwagę drugi warunek (8), otrzymujemy x n = 0. Dlatego zgodnie ze wzorem (9) x n = h n.

Następnie, zgodnie ze wzorem (9), niewiadome x n -1, x n -2, ..., x 1 są kolejno znajdowane. Ten etap obliczeń nazywa się biegiem wstecznym, podczas gdy obliczanie współczynników przemiatania nazywa się przemiataniem do przodu.

Dla pomyślnego zastosowania metody przemiatania konieczne jest, aby w procesie obliczeń nie było sytuacji z dzieleniem przez zero, a przy dużych wymiarach układów nie powinno być gwałtownego wzrostu błędów zaokrągleń. Zadzwonimy do biegu prawidłowy jeśli mianownik współczynników przemiatania (10) nie znika, oraz zrównoważony jeśli ½x ja ½<1 при всех i=1,2,…, n. Достаточные условия корректности и устойчивости прогонки, которые во многих приложениях выполняются, определяются теоремой.

Twierdzenie. Niech współczynniki a i oraz c i równania (7) dla i = 2,3, ..., n-1 różnią się od zera i niech

½b i ½> ½a i ½ + ½c i ½ dla i = 1, 2, ..., n. (jedenaście)

Wtedy przemiatanie określone wzorami (10), (9) jest poprawne i stabilne.