Sin x are un grafic. Funcțiile y = sin x, y = cos x, proprietățile și graficele lor - Knowledge Hypermarket

În această lecție, vom arunca o privire mai atentă la funcția y = sin x, la proprietățile ei de bază și la grafic. La începutul lecției, vom da definiția unei funcții trigonometrice y = sin t pe cercul de coordonate și vom considera graficul funcției pe un cerc și o dreaptă. Să arătăm periodicitatea acestei funcții pe grafic și să luăm în considerare principalele proprietăți ale funcției. La sfârșitul lecției, vom rezolva mai multe sarcini simple folosind graficul unei funcții și proprietățile acesteia.

Tema: Funcții trigonometrice

Lecția: Funcția y = sinx, proprietățile ei de bază și graficul

Când luați în considerare o funcție, este important să atribuiți fiecare valoare a argumentului unei singure valori de funcție. Acest legea conformitatiiși se numește funcție.

Să definim legea corespondenței pentru.

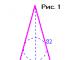
Orice număr real corespunde unui singur punct pe cerc unitar Un punct are o singură ordonată, care se numește sinusul unui număr (Fig. 1).

Fiecare valoare de argument este asociată cu o singură valoare a funcției.

Proprietăți evidente rezultă din definiția sinusului.

Figura arată că de cand aceasta este ordonata unui punct de pe cercul unitar.

Luați în considerare graficul unei funcții. Să ne amintim interpretarea geometrică a argumentului. Argumentul este unghiul central, măsurat în radiani. Pe axă, vom reprezenta numere reale sau unghiuri în radiani, pe axă, valorile corespunzătoare ale funcției.

De exemplu, unghiul de pe cercul unității corespunde unui punct de pe grafic (Fig. 2)

Am obținut graficul funcției pe site Dar cunoscând perioada sinusului, putem reprezenta graficul funcției pe întregul domeniu de definiție (Fig. 3).

Perioada principală a funcției este. Aceasta înseamnă că graficul poate fi obținut pe un segment și apoi continua la întregul domeniu de definiție.

Luați în considerare proprietățile funcției:

1 Domeniul de aplicare:

2) Interval de valori:

3) Funcția este impară:

4) Cea mai mică perioadă pozitivă:

5) Coordonatele punctelor de intersecție ale graficului cu axa absciselor:

6) Coordonatele punctului de intersecție al graficului cu axa y:

7) Intervalele la care funcția ia valori pozitive:

8) Intervalele la care funcția ia valori negative:

9) Intervale crescătoare:

10) Intervale descrescătoare:

11) Puncte minime:

12) Funcție minimă:

13) Puncte maxime:

14) Funcție maximă:

Am examinat proprietățile funcției și graficul acesteia. Proprietățile vor fi folosite în mod repetat la rezolvarea problemelor.

Bibliografie

1. Algebra și începutul analizei, nota 10 (în două părți). Manual pentru instituțiile de învățământ ( nivel de profil) ed. A.G. Mordkovici. -M .: Mnemosina, 2009.

2. Algebra și începutul analizei, nota 10 (în două părți). Cartea de probleme pentru instituțiile de învățământ (nivel de profil), ed. A.G. Mordkovici. -M .: Mnemosina, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Schwarzburd S.I. Algebră și calcul pentru clasa a 10-a ( tutorial pentru elevii școlilor și claselor cu studiu aprofundat al matematicii) .- M .: Educație, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartburd S.I. Studiu aprofundat al algebrei și analizei matematice.-M .: Educație, 1997.

5. Culegere de probleme de matematică pentru solicitanții instituțiilor de învățământ superior (sub redacția MI Skanavi) .- M.: Liceu, 1992.

6. Merzlyak A.G., Polonskiy VB, Yakir M.S. Simulator algebric.-K .: A.S.K., 1997.

7. Sahakyan S.M., Goldman A.M., Denisov D.V. Sarcini în algebră și principiile analizei (un ghid pentru elevii din clasele 10-11 din instituțiile de învățământ general) .- M .: Educație, 2003.

8. Karp A.P. Culegere de probleme de algebră și principiile analizei: manual. indemnizatie pentru 10-11 clase cu adâncire studiu Matematică.-M .: Educaţie, 2006.

Teme pentru acasă

Algebra și începutul analizei, nota 10 (în două părți). Cartea de probleme pentru instituțiile de învățământ (nivel de profil), ed.

A.G. Mordkovici. -M .: Mnemosina, 2007.

№№ 16.4, 16.5, 16.8.

Resurse web suplimentare

3. Portal educațional a se pregăti pentru examene ().

Inapoi inainte

Atenţie! Previzualizările diapozitivelor au doar scop informativ și este posibil să nu reprezinte toate opțiunile de prezentare. Dacă sunteți interesat de această lucrare, vă rugăm să descărcați versiunea completă.

Fierul rugineste, fara a se folosi de el insusi,
apa stătătoare putrezește sau îngheață la frig,
iar mintea unei persoane, negăsind nici un folos pentru ea însăși, se ofilește.
Leonardo da Vinci

Tehnologii utilizate:învățare cu probleme, gândire critică, comunicare comunicativă.

Obiective:

• Dezvoltarea interesului cognitiv pentru învățare.
• Studiul proprietăților funcției y = sin x.
• Formarea deprinderilor practice pentru construirea unui grafic al funcției y = sin x pe baza materialului teoretic studiat.

Sarcini:

1. Utilizați potențialul existent de cunoștințe despre proprietățile funcției y = sin x în situații specifice.

2. Aplicați stabilirea conștientă a conexiunilor între modelele analitice și geometrice ale funcției y = sin x.

Dezvoltați inițiativa, o anumită dorință și interes în găsirea unei soluții; capacitatea de a lua decizii, nu te opri aici, apără-ți punctul de vedere.

Să promoveze la elevi activitatea cognitivă, simțul responsabilității, respectul unul față de celălalt, înțelegerea reciprocă, sprijinul reciproc, încrederea în sine; cultura comunicarii.

În timpul orelor

Etapa 1. Actualizarea cunoștințelor de bază, motivația de a studia materiale noi

„Intrarea în lecție”.

Pe tablă sunt scrise 3 afirmații:

1. Ecuația trigonometrică sin t = a are întotdeauna o soluție.
2. O funcție impară poate fi reprezentată prin transformarea simetriei în jurul axei y.
3. O funcție trigonometrică poate fi reprezentată folosind o jumătate de undă principală.

Elevii discută în perechi: Sunt afirmațiile corecte? (1 minut). Rezultatele discuției inițiale (da, nu) sunt apoi introduse în tabelul din coloana „Înainte”.

Profesorul stabilește scopurile și obiectivele lecției.

2. Actualizarea cunoștințelor (frontal pe modelul cercului trigonometric).

Am întâlnit deja funcția s = sin t.

1) Ce valori poate lua variabila t. Care este scopul acestei funcții?

2) În ce interval se află valorile expresiei sin t. Aflați cele mai mari și cele mai mici valori ale funcției s = sin t.

3) Rezolvați ecuația sin t = 0.

4) Ce se întâmplă cu ordonata unui punct când se mișcă de-a lungul primului sfert? (ordonata crește). Ce se întâmplă cu ordonata unui punct când se mișcă de-a lungul celui de-al doilea sfert? (ordonata scade treptat). Cum se leagă acest lucru cu monotonitatea funcției? (funcția s = sin t crește pe segment și scade pe segment).

5) Să scriem funcția s = sin t în forma obișnuită pentru noi y = sin x (vom construi în sistemul obișnuit de coordonate xOy) și să alcătuim un tabel cu valorile acestei funcție.

X	0
la	0			1			0

Etapa 2. Percepție, înțelegere, consolidare primară, memorare involuntară

Etapa 4. Sistematizarea primară a cunoștințelor și metodelor de activitate, transferul și aplicarea acestora în situații noi

6.Nr. 10.18 (b, c)

Etapa 5. Control final, corectare, evaluare și autoevaluare

7. Revenind la enunțuri (începutul lecției), discutați despre utilizarea proprietăților funcției trigonometrice y = sin x și completați coloana „După” din tabel.

8. D / z: p.10, nr. 10.7 (a), 10.8 (b), 10.11 (b), 10.16 (a)

Lecție și prezentare pe tema: „Funcția y = sin (x). Definiții și proprietăți”

Materiale suplimentare
Dragi utilizatori, nu uitați să lăsați comentariile, recenziile, urările! Toate materialele au fost verificate de un program antivirus.

Manuale si simulatoare in magazinul online Integral pentru nota 10 din 1C
Rezolvăm probleme de geometrie. Teme interactive de clădire pentru clasele 7-10
Mediul software „1C: Mathematical Constructor 6.1”

Ce vom studia:

• Proprietățile funcției Y = sin (X).
• Graficul funcției.
• Cum se construiește un grafic și scara acestuia.
• Exemple.

Proprietăți sinusoidale. Y = păcat (X)

Băieți, ne-am familiarizat deja cu funcțiile trigonometrice ale unui argument numeric. Îți amintești de ei?

Să aruncăm o privire mai atentă la funcția Y = sin (X)

Să notăm câteva proprietăți ale acestei funcții:
1) Domeniul definiției - un set de numere reale.
2) Funcția este impară. Să ne amintim definiția unei funcții impare. O funcție se numește impară dacă egalitatea este valabilă: y (-x) = - y (x). După cum ne amintim din formulele fantomă: sin (-x) = - sin (x). Definiția a fost îndeplinită, deci Y = sin (X) este o funcție impară.
3) Funcția Y = sin (X) crește pe segment și scade pe segment [π / 2; π]. Când ne deplasăm de-a lungul primului sfert (în sens invers acelor de ceasornic), ordonata crește, iar când ne deplasăm de-a lungul celui de-al doilea sfert, aceasta scade.

4) Funcția Y = sin (X) este mărginită de jos și de sus. Această proprietate rezultă din faptul că
-1 ≤ sin (X) ≤ 1
5) Cea mai mică valoare a funcției este -1 (la x = - π / 2 + πk). Cea mai mare valoare a funcției este 1 (la x = π / 2 + πk).

Să folosim proprietățile 1-5 pentru a reprezenta grafic funcția Y = sin (X). Ne vom construi graficul secvenţial folosind proprietăţile noastre. Să începem să construim un grafic pe un segment.

O atenție deosebită trebuie acordată scalei. Pe ordonată este mai convenabil să luați un segment unitar egal cu 2 celule, iar pe axa absciselor - să luați un segment unitar (două celule) egal cu π / 3 (vezi figura).

Trasează funcția sinus x, y = sin (x)

Să calculăm valorile funcției pe segmentul nostru:

Să construim un grafic pe baza punctelor noastre, ținând cont de a treia proprietate.

Tabel de conversie pentru formule fantomă

Să folosim a doua proprietate, care spune că funcția noastră este impară, ceea ce înseamnă că poate fi reflectată simetric față de origine:

Știm păcat (x + 2π) = sin (x). Aceasta înseamnă că pe segmentul [- π; π] graficul arată la fel ca pe segmentul [π; 3π] sau sau [-3π; - π] și așa mai departe. Ne rămâne să redesenăm cu atenție graficul din figura anterioară pe toată axa absciselor.

Graficul funcției Y = sin (X) se numește sinusoid.

Să mai scriem câteva proprietăți conform graficului construit:
6) Funcția Y = sin (X) crește pe orice segment de forma: [- π / 2 + 2πk; π / 2 + 2πk], k este un număr întreg și scade pe orice segment de forma: [π / 2 + 2πk; 3π / 2 + 2πk], k este un număr întreg.
7) Funcția Y = sin (X) este o funcție continuă. Să ne uităm la graficul funcției și să ne asigurăm că funcția noastră nu are discontinuități, ceea ce înseamnă continuitate.
8) Interval de valori: segment [- 1; unu]. Acest lucru se vede clar și din graficul funcției.
9) Funcția Y = sin (X) este o funcție periodică. Să ne uităm din nou la grafic și să vedem că funcția ia aceleași valori la anumite intervale.

Exemple de probleme cu sinus

1. Rezolvați ecuația sin (x) = x-π

Rezolvare: Să construim 2 grafice ale funcției: y = sin (x) și y = x-π (vezi figura).
Graficele noastre se intersectează într-un punct A (π; 0), acesta este răspunsul: x = π

2. Reprezentați grafic funcția y = sin (π / 6 + x) -1

Rezolvare: Graficul dorit se obține prin mutarea graficului funcției y = sin (x) cu π / 6 unități la stânga și 1 unitate în jos.

Rezolvare: Să construim un grafic al funcției și să considerăm segmentul nostru [π / 2; 5π / 4].
Graficul funcției arată că cele mai mari și cele mai mici valori sunt atinse la capetele segmentului, în punctele π / 2 și, respectiv, 5π / 4.
Răspuns: sin (π / 2) = 1 este cea mai mare valoare, sin (5π / 4) = cea mai mică valoare.

Probleme sinusoidale pentru rezolvare independentă

• Rezolvați ecuația: sin (x) = x + 3π, sin (x) = x-5π
• Reprezentați grafic funcția y = sin (π / 3 + x) -2
• Trasează funcția y = sin (-2π / 3 + x) +1
• Aflați cea mai mare și cea mai mică valoare a funcției y = sin (x) pe un interval
• Aflați cea mai mare și cea mai mică valoare a funcției y = sin (x) pe segmentul [- π / 3; 5π / 6]

>> Matematică: Funcțiile y = sin x, y = cos x, proprietățile și graficele lor

Funcțiile y = sin x, y = cos x, proprietățile și graficele lor

În această secțiune vom discuta câteva proprietăți ale funcțiilor y = sin x, y= cos x și construiți graficele lor.

1. Funcția y = sin X.

Mai sus, în Secțiunea 20, am formulat o regulă care permite fiecărui număr t să asocieze numărul cos t, i.e. a caracterizat funcţia y = sin t. Să notăm câteva dintre proprietățile sale.

Proprietățile funcției u = sin t.

Domeniul de definiție este mulțimea K de numere reale.
Aceasta rezultă din faptul că orice număr 2 corespunde punctului M (1) de pe cercul numeric, care are o ordonată bine definită; această ordonată este cos t.

u = sin t este o funcție impară.

Aceasta rezultă din faptul că, după cum sa dovedit în § 19, pentru orice t egalitatea
Prin urmare, graficul funcției u = sin t, ca și graficul oricărei funcții impare, este simetric față de originea la sistem dreptunghiular coordonatele tO si.

Funcția u = sin t crește pe segment
Aceasta rezultă din faptul că atunci când punctul se deplasează de-a lungul primului sfert al cercului numeric, ordonata crește treptat (de la 0 la 1 - vezi Fig. 115), iar când punctul se deplasează de-a lungul celui de-al doilea sfert al cercului numeric, ordonata scade treptat (de la 1 la 0 - vezi Fig. 115).fig. 116).

Funcția u = sin t este mărginită atât de jos, cât și de sus. Aceasta rezultă din faptul că, după cum am văzut în § 19, pentru orice t inegalitatea

(funcția atinge această valoare în orice punct al formularului (funcția atinge această valoare în orice punct al formularului
Folosind proprietățile obținute, vom construi un grafic al funcției care ne interesează. Dar (atentie!) In loc de u - sin t vom scrie y = sin x (la urma urmei, suntem mai obisnuiti sa scriem y = f (x), si nu u = f (t)). Aceasta înseamnă că vom construi graficul în sistemul obișnuit de coordonate xOy (și nu tOy).

Să compunem un tabel de valori ale funcției y - sin x:

Cometariu.

Iată una dintre versiunile de origine a termenului „sinus”. În latină, sinus înseamnă îndoire (coarda arcului).

Graficul trasat justifică această terminologie într-o oarecare măsură.

Linia care servește ca grafic al funcției y = sin x se numește sinusoid. Acea parte a sinusoidei, care este prezentată în Fig. 118 sau 119, se numește undă sinusoidală, iar acea parte a sinusoidului, care este prezentată în Fig. 117 se numește arc de semiundă sau arc sinusoidal.

2. Funcția y = cos x.

Studiul funcției y = cos x ar putea fi efectuat aproximativ după aceeași schemă folosită mai sus pentru funcția y = sin x. Dar vom alege calea care duce la obiectiv mai repede. În primul rând, vom demonstra două formule care sunt importante în sine (veți vedea asta la liceu), dar până acum au doar un sens auxiliar pentru scopurile noastre.

Pentru orice valoare a lui t, egalitățile

Dovada... Fie numărul t să corespundă punctului M al cercului numeric n și numărului * + - punctul P (Fig. 124; de dragul simplității, am luat punctul M în primul trimestru). Arcele AM ​​și BP sunt egale, iar triunghiurile dreptunghiulare OKM și OLP sunt egale. Prin urmare, O K = Ob, MK = Pb. Din aceste egalități și din locația triunghiurilor OKM și OLP în sistemul de coordonate, tragem două concluzii:

1) ordonata punctului P, atât în ​​valoare absolută, cât și în semn, coincide cu abscisa punctului M; înseamnă că

2) abscisa punctului P este egală în valoare absolută cu ordonata punctului M, dar diferă de aceasta prin semn; înseamnă că

Raționamentul corespunzător se realizează aproximativ în același mod în cazurile în care punctul M nu aparține primului trimestru.
Să folosim formula (aceasta este formula dovedită mai sus, doar că în locul variabilei t folosim variabila x). Ce ne oferă această formulă? Ne permite să afirmăm că funcțiile

sunt identice, ceea ce înseamnă că graficele lor coincid.
Să diagramăm funcția Pentru a face acest lucru, apelăm la un sistem de coordonate auxiliar cu originea într-un punct (linia punctată este trasată în Fig. 125). Atașăm funcția y = sin x noului sistem de coordonate - acesta va fi graficul funcției (fig. 125), i.e. graficul funcției y - cos x. Ea, ca și graficul funcției y = sin x, se numește sinusoid (ceea ce este destul de natural).

Proprietățile funcției y = cos x.

y = cos x este o funcție pară.

Etapele construcției sunt prezentate în Fig. 126:

1) construim un grafic al funcției y = cos x (mai precis, o semiundă);
2) întinderea graficului trasat de pe axa x cu un factor de 0,5, obținem o jumătate de undă din graficul necesar;
3) folosind semiunda obținută, construim întregul grafic al funcției y = 0,5 cos x.

Conținutul lecției schița lecției suport cadru prezentarea lecției metode accelerative tehnologii interactive Practică sarcini și exerciții ateliere de autotestare, antrenamente, cazuri, quest-uri teme de discuție întrebări întrebări retorice de la elevi Ilustrații audio, clipuri video și multimedia fotografii, poze, diagrame, tabele, scheme umor, glume, glume, pilde cu benzi desenate, proverbe, cuvinte încrucișate, citate Suplimente rezumate articole jetoane pentru curioase fișe manuale manuale vocabular de bază și suplimentar al termenilor alții Îmbunătățirea manualelor și lecțiilorremedieri de erori în tutorial actualizarea unui fragment în manual elemente de inovare în lecție înlocuirea cunoștințelor învechite cu altele noi Doar pentru profesori lecții perfecte planul calendaristic pentru anul instrucțiuni agenda de discuții Lecții integrate

Am aflat că comportamentul funcțiilor trigonometrice și al funcțiilor y = sin x în special, pe întreaga linie numerică (sau pentru toate valorile argumentului X) este complet determinată de comportamentul său în interval 0 < X < π / 2 .

Prin urmare, în primul rând, vom reprezenta grafic funcția y = sin x tocmai în acest interval.

Să compunem următorul tabel cu valorile funcției noastre;

Marcând punctele corespunzătoare pe planul de coordonate și conectându-le cu o linie netedă, obținem curba prezentată în figură

Curba rezultată ar putea fi construită geometric, fără a compila un tabel cu valorile funcției y = sin x .

1. Împărțiți primul sfert de cerc cu raza 1 în 8 părți egale.Ordinele punctelor de împărțire ale cercului sunt sinusurile unghiurilor corespunzătoare.

2.Primul sfert de cerc corespunde unghiurilor de la 0 la π / 2 ... Prin urmare, pe axă X luați un segment și împărțiți-l în 8 părți egale.

3. Să desenăm linii drepte paralele cu axele X, iar din punctele de împărțire, vom restabili perpendicularele la intersecția cu liniile orizontale.

4. Conectați punctele de intersecție cu o linie netedă.

Acum să trecem la interval π / 2 < X < π .
Fiecare valoare de argument X din acest interval poate fi reprezentat ca

X = π / 2 + φ

Unde 0 < φ < π / 2 ... Prin formule de reducere

păcat ( π / 2 + φ ) = cos φ = păcat ( π / 2 - φ ).

Punctele axei X cu abscise π / 2 + φ și π / 2 - φ simetrice între ele în jurul punctului axei X cu abscisă π / 2 , iar sinusurile din aceste puncte sunt aceleași. Acest lucru vă permite să obțineți un grafic al funcției y = sin x în intervalul [ π / 2 , π ] prin simpla afisare simetrica a graficului acestei functii in intervalul relativ la dreapta X = π / 2 .

Acum folosind proprietatea funcţie impară y = sin x,

păcat (- X) = - păcat X,

este ușor să reprezentați această funcție în intervalul [- π , 0].

Funcția y = sin x este periodică cu o perioadă de 2π ;. Prin urmare, pentru a reprezenta întregul grafic al acestei funcții, curba prezentată în figură este suficientă, continuați la stânga și la dreapta periodic cu o perioadă 2π .

Curba rezultată se numește sinusoid ... Este graficul funcției y = sin x.

Figura ilustrează bine toate acele proprietăți ale funcției. y = sin x , care au fost anterior dovedite de noi. Să ne amintim aceste proprietăți.

1) Funcție y = sin x definit pentru toate valorile X , astfel încât domeniul definiției sale este colecția tuturor numerelor reale.

2) Funcția y = sin x limitat. Toate valorile pe care le ia sunt în intervalul -1 la 1, inclusiv aceste două numere. Prin urmare, intervalul de variație al acestei funcții este determinat de inegalitatea -1 < la < 1. Când X = π / 2 + 2k π funcția ia cele mai mari valori egal cu 1, iar pentru x = - π / 2 + 2k π - cele mai mici valori egale cu - 1.

3) Funcția y = sin x este impar (sinusoida este simetrică față de origine).

4) Funcția y = sin x periodic cu perioada 2 π .

5) În intervalele 2n π < X < π + 2n π (n este orice număr întreg) este pozitiv, iar în intervale π + 2k π < X < 2π + 2k π (k este orice număr întreg) este negativ. Pentru x = k π funcția dispare. Prin urmare, aceste valori ale argumentului x (0; ± π ; ± 2 π ; ...) se numesc zerouri ale funcției y = sin x

6) În intervalele - π / 2 + 2n π < X < π / 2 + 2n π funcţie y = sin X creste monoton, si in intervale π / 2 + 2k π < X < 3π / 2 + 2k π scade monoton.

Acordați o atenție deosebită comportamentului funcției. y = sin x punctul apropiat X = 0 .

De exemplu sin 0,012 ≈ 0,012; păcat (-0,05) ≈ -0,05;

sin 2 ° = sin π 2 / 180 = sin π / 90 ≈ 0,03 ≈ 0,03.

În același timp, trebuie remarcat faptul că pentru orice valoare a lui x

| păcat X| < | x | . (1)

Într-adevăr, să fie raza cercului prezentat în figură 1,
A / AОВ = X.

Apoi păcatul X= AC. Dar AC< АВ, а АВ, в свою очередь, меньше длины дуги АВ, на которую опирается угол X... Lungimea acestui arc este evident egală cu X, deoarece raza cercului este 1. Deci, la 0< X < π / 2

sin x< х.

Prin urmare, din cauza ciudățeniei funcției y = sin x este ușor să arăți că pentru - π / 2 < X < 0

| păcat X| < | x | .

În cele din urmă, la X = 0

| sin x | = | x |.

Astfel, pentru | X | < π / 2 inegalitatea (1) este demonstrată. De fapt, această inegalitate este valabilă și pentru | X | > π / 2 datorită faptului că | păcat X | < 1, a π / 2 > 1

Exerciții

1.On program y = sin x determina: a) sin 2; b) sin 4; c) păcatul (-3).

2.On program y = sin x determinați ce număr este din interval
[ - π / 2 , π / 2 ] are un sinus egal cu: a) 0,6; b) -0,8.

3. După programul de funcții y = sin x determinați ce numere au un sinus,
egal cu 1/2.

4. Aflați aproximativ (fără a folosi tabele): a) sin 1 °; b) sin 0,03;
c) sin (-0,015); d) păcat (-2 ° 30 ").