Care sunt semnele că triunghiurile sunt egale? Primul semn al egalității triunghiurilor

O figură geometrică formată din trei segmente care leagă trei puncte care nu aparțin aceleiași drepte.

Laturile triunghiului formează trei unghiuri la vârfurile triunghiului. Pentru a parafraza, triunghi este un poligon care are trei unghiuri .

Semnificație practică semne de egalitate a triunghiurilor se rezumă la următoarele: conform formulării triunghiurile sunt egale, în cazul în care este posibil să le suprapunem una peste alta astfel încât să coincidă; cu toate acestea, implementarea suprapunerii triunghiului poate fi uneori dificilă și uneori imposibilă.

Testele pentru egalitatea triunghiurilor fac posibilă înlocuirea suprapunerii triunghiurilor prin găsirea și compararea componentelor fundamentale individuale (laturile și unghiurile) și justifică astfel egalitatea triunghiurilor.

3. Toate cele trei părți:

Ele evidențiază, de asemenea al patrulea semn, care nu este la fel de larg acoperit în cursul de matematică al școlii precum cele trei anterioare. Este formulat astfel:

Dacă două laturi ale primului triunghi sunt, respectiv, egale cu două laturi ale celui de-al doilea triunghi, iar unghiul opus celei mai mari laturi din primul triunghi este egal cu unghiul opus laturii corespunzătoare egal cu acesta în al doilea triunghi, atunci acestea triunghiurile sunt egale.

Semne de egalitate a triunghiurilor

Triunghiurile ale căror laturi corespunzătoare sunt egale se numesc congruente.

Teoremă (primul semn al egalității triunghiurilor).
Dacă două laturi și unghiul dintre ele ale unui triunghi sunt, respectiv, egale cu două laturi și unghiul dintre ele ale altui triunghi, atunci astfel de triunghiuri sunt congruente.

Teoremă (al doilea criteriu pentru egalitatea triunghiurilor).
Dacă o latură și două unghiuri adiacente ale unui triunghi sunt egale cu o latură și, respectiv, două unghiuri adiacente ale altui triunghi, atunci astfel de triunghiuri sunt congruente.

Teorema (al treilea criteriu pentru egalitatea triunghiurilor).
Dacă trei laturi ale unui triunghi sunt, respectiv, egale cu trei laturi ale altui triunghi, atunci astfel de triunghiuri sunt congruente.

Semne de asemănare ale triunghiurilor

Triunghiurile ale căror unghiuri sunt egale și ale căror laturi similare sunt proporționale se numesc similare: , unde este coeficientul de similitudine.

Eu semnez asemănarea triunghiurilor. Dacă două unghiuri ale unui triunghi sunt, respectiv, egale cu două unghiuri ale altuia, atunci aceste triunghiuri sunt similare.

II semn al asemănării triunghiurilor. Dacă trei laturi ale unui triunghi sunt proporționale cu trei laturi ale altui triunghi, atunci triunghiurile sunt similare.

III semnul asemănării triunghiurilor. Dacă două laturi ale unui triunghi sunt proporționale cu două laturi ale altui triunghi, iar unghiurile dintre aceste laturi sunt egale, atunci triunghiurile sunt similare.

1) pe două laturi și unghiul dintre ele

Dovada:

Fie triunghiurile ABC și A 1 B 1 C 1 să aibă unghiul A egal cu unghiul A 1, AB egal cu A 1 B 1, AC egal cu A 1 C 1. Să demonstrăm că triunghiurile sunt congruente.

Să impunem triunghiul ABC (sau simetric cu acesta) pe triunghiul A 1 B 1 C 1 astfel încât unghiul A să fie aliniat cu unghiul A 1 . Deoarece AB=A 1 B 1 și AC=A 1 C 1, atunci B va coincide cu B 1, iar C va coincide cu C 1. Aceasta înseamnă că triunghiul A 1 B 1 C 1 coincide cu triunghiul ABC și, prin urmare, este egal cu triunghiul ABC.

Teorema este demonstrată.

2) de-a lungul colțurilor laterale și adiacente

Dovada:

Fie ABC și A 1 B 1 C 1 două triunghiuri în care AB este egal cu A 1 B 1, unghiul A este egal cu unghiul A 1 și unghiul B este egal cu unghiul B 1. Să demonstrăm că sunt egali.

Să impunem triunghiul ABC (sau simetric cu acesta) pe triunghiul A 1 B 1 C 1 astfel încât AB să coincidă cu A 1 B 1. Deoarece ∠BAC =∠B 1 A 1 C 1 și ∠ABC=∠A 1 B 1 C 1, atunci raza AC va coincide cu A 1 C 1 și BC va coincide cu B 1 C 1. Rezultă că vârful C coincide cu C 1. Aceasta înseamnă că triunghiul A 1 B 1 C 1 coincide cu triunghiul ABC și, prin urmare, este egal cu triunghiul ABC.

Teorema este demonstrată.

3) pe trei laturi

Dovada:

Luați în considerare triunghiurile ABC și A l B l C 1, în care AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Să demonstrăm că ΔАВС =ΔA 1 B 1 C 1.

Să aplicăm triunghiul ABC (sau simetric cu acesta) la triunghiul A 1 B 1 C 1 astfel încât vârful A să fie aliniat cu vârful A 1, vârful B să fie aliniat cu vârful B 1, iar vârfurile C și C 1 să fie pe laturile opuse ale dreptei A 1 B 1. Să luăm în considerare 3 cazuri:

1) Raza C 1 C trece în interiorul unghiului A 1 C 1 B 1. Deoarece, conform condițiilor teoremei, laturile AC și A 1 C 1, BC și B 1 C 1 sunt egale, atunci triunghiurile A 1 C 1 C și B 1 C 1 C sunt isoscele. După teorema proprietății unghiurilor unui triunghi isoscel, ∠1 = ∠2, ∠3 = ∠4, deci ∠ACB=∠A 1 C 1 B 1 .

2) Raza C 1 C coincide cu una dintre laturile acestui unghi. A se află pe CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - isoscel, ∠ACB=∠A 1 C 1 B 1.

3) Raza C 1 C trece în afara unghiului A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, ceea ce înseamnă ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

Deci, AC=A 1 C 1, BC=B 1 C 1, ∠C=∠C 1. Prin urmare, triunghiurile ABC și A 1 B 1 C 1 sunt egale în
primul criteriu pentru egalitatea triunghiurilor.

Teorema este demonstrată.

2. Împărțirea unui segment în n părți egale.

Desenați o rază prin A, așezați n segmente egale pe ea. Desenați o dreaptă prin B și A n și linii paralele cu aceasta prin punctele A 1 - A n -1. Să le marchem punctele de intersecție cu AB. Obținem n segmente care sunt egale conform teoremei lui Thales.

teorema lui Thales. Dacă mai multe segmente egale sunt așezate succesiv pe una dintre cele două linii și sunt trasate linii paralele prin capetele lor care intersectează a doua linie, atunci acestea vor tăia segmente egale de pe a doua linie.

Dovada. AB=CD

1. Desenați linii drepte prin punctele A și C paralele cu cealaltă parte a unghiului. Obținem două paralelograme AB 2 B 1 A 1 și CD 2 D 1 C 1. După proprietatea unui paralelogram: AB 2 = A 1 B 1 și CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 și sunt egale pe baza celui de-al doilea criteriu pentru egalitatea triunghiurilor:
AB = CD conform teoremei,
ca corespunzătoare, formate la intersecția dreptei paralele BB 1 și DD 1 BD.

3. În mod similar, fiecare dintre unghiuri se dovedește a fi egal cu unghiul cu vârful în punctul de intersecție al secantelor. AB 2 = CD 2 ca elemente corespunzătoare în triunghiuri congruente.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Podgorny Maxim

Materialul de hârtie de cercetare poate fi folosit pentru cluburile de geometrie din clasa a VII-a

Descarca:

Previzualizare:

MBU DO al orașului Rostov-pe-Don „Palatul creativității copiilor și tinerilor”

Don Academia de Științe pentru Tineri Cercetători numit după. Yu. A. Zhdanova

Matematică

Subiect: „Teoreme non-standard privind egalitatea triunghiurilor”

Podgorny Maxim, clasa a VII-a,

Școala Gimnazială MBOU nr. 3,

supraveghetor:

Oleynikov Lyudmila Aleksandrovna,

profesor de matematică,

Școala Gimnazială MBOU nr. 3,

Salsk, regiunea Rostov

Rostov-pe-Don

2017

Introducere…………………………………………………………………………………… 3

Parte principală

Semne de egalitate a triunghiurilor…………………………………………………… 4

Semne nestandard de egalitate a triunghiurilor………………………….7

Concluzie……………………………………………………………………………… 10

Referințe………………………………………………………………… 11

Aplicație

Introducere.

Relevanţă:

Triunghiul este una dintre figurile principale în planimetrie. Am auzit multe de la liceeni că atunci când se pregătesc pentru Examenul Unificat de Stat, de multe ori trebuie să demonstreze egalitatea triunghiurilor. Și cunoașterea semnelor de bază se dovedește a fi insuficientă. Am vrut să știu dacă este posibil să demonstrez egalitatea triunghiurilor folosind alți parametri. În manualul de geometrie, din care studiază elevii școlii noastre (autori L.S. Atanasyan, V.F. Butuzov etc. Geometrie 7-9), sunt luate în considerare doar 3 semne de egalitate a triunghiurilor. Am căutat prin truse didactice de la alți autori. Dar chiar și în ele sunt propuse spre studiu doar trei teoreme binecunoscute.

Ipoteză:

Se pot formula, pe lângă cele trei cunoscute, și alte criterii de egalitate a triunghiurilor?

Pentru a mă asigura că răspunsul la această întrebare nu mă privește numai pe mine, am realizat un sondaj sociologic în rândul elevilor din clasele 7-11 (vezi Anexa 1).

Ipotezele mele au fost confirmate. Majoritatea elevilor cunosc doar trei semne că triunghiurile sunt egale.

Astfel, scopul cercetării mele a fost de a găsi noi semne de egalitate a triunghiurilor.

Sarcini:

Θ Studiați literatura de specialitate pe tema studiată.

ΘSpecificați numărul de semne că triunghiurile sunt egale.

ΘDemonstrați colegilor și elevilor școlii noastre existența altor semne de egalitate a triunghiurilor și posibilitatea de a le dovedi.

Obiectul de studiu:

Studierea semnelor de egalitate a triunghiurilor.

Subiect de studiu. Triunghiul este una dintre figurile principale în planimetrie.

Metodă de cercetare:Teoretic (studiu, analiză și sinteză), sistem-căutare, practic (dovada teoremelor).

Referință istorică

Triunghiul este una dintre figurile centrale ale întregii geometrii.

La rezolvarea problemelor, se utilizează marea sa varietate de proprietăți.

Proprietățile unui triunghi sunt utilizate pe scară largă în practică: în arhitectură; la elaborarea unui desen al clădirii, la planificarea viitoarelor apartamente; în industrie, în proiectarea diferitelor piese, în fabricarea materialelor de construcție, în construcția de nave și aeronave; în navigație pentru a trasa traseul corect și cel mai precis; în astrologie și astronomie, triunghiul este o figură foarte semnificativă; Triunghiurile fac structurile liniilor electrice de înaltă tensiune și ale podurilor feroviare fiabile.

În plus, există multe alte zone în care sunt utilizate diverse proprietăți ale unui triunghi: atunci când începeți un joc de biliard, trebuie să aranjați bilele sub formă de triunghi, pentru aceasta folosesc un dispozitiv special; plasarea acelor în jocul de bowling este tot sub forma unui triunghi echilateral; triunghiurile sunt folosite pentru a crea podele frumoase cu parchet; dispozitivul triunghiului lui Pascal: fiecare număr este egal cu suma celor două numere situate deasupra lui (încercuiește cele trei numere cu un triunghi). Totul este elementar, dar câte minuni se ascund în el! Computerul a tradus triunghiul lui Pascal în limbajul culorii.

Tema triunghiului poate fi continuată la infinit.

Sunt atât de multe triunghiuri în lume!

Există, de asemenea, semnificații figurative ale acestei figuri: de exemplu, regula „triunghiului de aur” se bazează pe psihologia cumpărătorului - după ce a găsit produsul de care are nevoie, cumpărătorul se grăbește la casă. Sarcina vânzătorilor este de a-l face să stea mai mult în magazin prin plasarea bunurilor de care are nevoie cumpărătorul la vârfurile unui triunghi imaginar, adică să-l „ancoreze” pe cumpărător. Cu cât aria triunghiului este mai mare, cu atât aspectul magazinului poate fi numit mai de succes. Într-un magazin alimentar, aceste produse ancoră sunt gastronomia, produsele lactate și pâinea. Peretele din spate al zonei de vânzare este al doilea loc ca importanță și acolo este cel mai indicat să plasați produse de ancorare - tocmai pentru a-l obliga pe cumpărător să parcurgă tot perimetrul magazinului.

Cunoscutul Triunghi al Bermudelor este o zonă din Oceanul Atlantic în care se presupune că au loc dispariții misterioase de nave și avioane. Zona este delimitată de linii de la Florida la Bermuda, la Puerto Rico și înapoi la Florida prin Bahamas.

Prin urmare, studiul unui triunghi și al tuturor proprietăților sale este un subiect foarte relevant.

Scopul acestei lucrări este de a vorbi despre semnele de egalitate ale triunghiurilor, care este una dintre cele mai importante proprietăți ale acestora.

Testele pentru egalitatea triunghiurilor sunt teoreme pe baza cărora se poate demonstra că uneletriunghiuri sunt egale.

În geometrie, sunt folosite trei semne de egalitate a triunghiurilor.

Acest subiect a fost studiat practic, deoarece astăzi există trei criterii pentru egalitatea triunghiurilor, care pot fi dovedite folosind teoremele corespunzătoare.

În antichitate, odată cu astronomia, a apărut știința trigonometriei. Cuvântul „trigonometrie” este derivat din grecescul „triunghi” și „măsură”. Sensul literal este „știința măsurării triunghiurilor”.

Folosind frânghii întinse lungi de 3, 4 și 5 unități, preoții egipteni au obținut unghiuri drepte la construirea templelor etc.

Arta de a înfățișa obiecte într-un avion a atras atenția omului din cele mai vechi timpuri oamenii pictau diverse ornamente, plante și animale pe stânci, pereți, vase și alte obiecte de uz casnic. Oamenii au căutat să se asigure că imaginea reflectă corect forma naturală a obiectului.

Doctrina asemănării figurilor bazată pe teoria relațiilor și proporțiilor a fost creată în Grecia Antică în secolele V-IV î.Hr. și există și se dezvoltă și astăzi. De exemplu, există o mulțime de jucării pentru copii similare cu articolele din lumea adulților, pantofii și hainele de același stil sunt disponibile în diferite dimensiuni. Aceste exemple pot fi continuate mai departe. În cele din urmă, toți oamenii sunt asemănători unii cu alții și, după cum spune Biblia, Dumnezeu i-a creat după chipul și asemănarea Sa.

Testele pentru egalitatea triunghiurilor au fost de multă vreme de mare importanță în geometrie, deoarece demonstrarea numeroaselor teoreme s-a redus la demonstrarea egalității anumitor triunghiuri. Pitagoreii erau deja angajați în demonstrarea semnelor egalității triunghiurilor. Potrivit lui Proclu, Eudemus din Rhodos îi atribuie lui Thales din Milet o dovadă a egalității a două triunghiuri având laturile egale și două unghiuri adiacente acestuia (al doilea semn al egalității triunghiurilor).

Thales a folosit această teoremă pentru a determina distanța de la țărm până la navele maritime.Nu se știe exact ce metodă a folosit Thales pentru a face acest lucru.

Semne de egalitate a triunghiurilor.

Să începem cu o definiție. Triunghiurile ABC și A1B1C1 se numesc egale dacă pot fi combinate prin suprapunere.

Un triunghi este format din șase elemente: trei unghiuri și trei laturi.

Aceasta ridică întrebarea: „Care este cel mai mic număr de elemente triunghiulare necesare pentru a stabili egalitatea a două triunghiuri?”

Nu vom putea stabili egalitatea a două triunghiuri pe baza unui element, deoarece este necunoscut: „Vor fi elementele rămase egale?”

De asemenea, este imposibil să se stabilească egalitatea a două triunghiuri folosind două elemente din cauza lipsei de informații pentru a stabili egalitatea.

Este posibil să se stabilească egalitatea a două triunghiuri folosind trei elemente. Dar acest lucru ridică întrebarea: „Ce exact trei elemente trebuie să fie numite pentru a stabili egalitatea triunghiurilor?”

Când am studiat această problemă, m-am uitat prin manuale școlare de geometrie ale diverșilor autori, precum și dicționare și cărți de referință. În manualele pentru clasa a VII-a sunt propuse spre studiu doar trei criterii pentru egalitatea triunghiurilor.

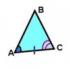
Θ1 Semn : Dacă două laturi și unghiul dintre ele ale unui triunghi sunt, respectiv, egale cu două laturi și unghiul dintre ele ale altui triunghi, atunci astfel de triunghiuri sunt congruente. Fig.1

Dovada. Luați în considerare triunghiuri ABC și A 1 B 1 C 1 , (Fig. 1) pentru care AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 . Să demonstrăm că ΔABC = ΔA 1 B 1 C 1 .

Deoarece ∠A = ∠A 1 , atunci triunghiul ABC poate fi suprapus triunghiului A 1 B 1 C 1 astfel încât vârful A coincide cu vârful A 1 , iar laturile AB și AC se vor suprapune razelor A, respectiv 1 B 1 şi A 1 C 1 . Deoarece AB = A 1 B 1, AC = A 1 C 1 , atunci latura AB se va alinia cu latura A 1 în 1 iar latura AC este cu latura A 1 C 1 ; în special, punctele B și B vor coincide 1, C și C 1 . Prin urmare, laturile BC și B vor coincide 1 C 1 . Deci, triunghiurile ABC și A 1 B 1 C 1 sunt complet compatibile, ceea ce înseamnă că sunt egale.

Și iată cum a fost folosit primul semn de egalitate a triunghiurilor în Egiptul Antic (pe două laturi și unghiul dintre ele), Thales din Milet este considerat și creatorul său, pentru a măsura înălțimea piramidei: imaginați-vă că stăm în fața unei piramide uriașe, cum putem măsura înălțimea ei? La urma urmei, nu îi puteți atașa instrumente de măsurare! Și aici primul semn de egalitate a triunghiurilor vine în ajutorul lui Thales din Milet: el a așteptat până când umbra sa a coincis exact cu înălțimea sa, a aplicat teorema, s-a dovedit că înălțimea piramidei este egală cu umbra ei (Fig. 2).

Orez. 2

Semnul Θ2: Dacă o latură și două unghiuri adiacente ale unui triunghi sunt egale cu o latură și, respectiv, două unghiuri adiacente ale altui triunghi, atunci astfel de triunghiuri sunt congruente.

Dovada: Dacă în △ABC și △A 1 B 1 C 1 vor avea loc următoarele egalităţi AB=A 1 B 1, ∠BAC=∠B 1 A 1 C 1, ∠АВС= ∠А 1 B 1 C 1 . Să punem triunghiurile A unul peste altul 1 B 1 C 1 și ABC astfel încât laturile egale AB și A să coincidă 1 în 1 și colțurile care le sunt adiacente. Ca și în exemplul anterior deja discutat, dacă este necesar, triunghiul A 1 B 1 C 1 Poți „întoarce-l și pune-l pe cealaltă parte”. Triunghiurile vor coincide, prin urmare, pot fi considerate egale.

Θ3 Semn : Dacă trei laturi ale unui triunghi sunt, respectiv, egale cu trei laturi ale altui triunghi, atunci astfel de triunghiuri sunt congruente. Dovada: Fiți pentru △ABC și △A 1 B 1 C 1 egalitățile A sunt valabile 1 B 1 =AB, B 1 C 1 =BC, C 1 A 1 =SA. Să mutăm triunghiul A 1 B 1 C 1 deci partea aceea A 1 în 1 coincide cu latura AB și cu vârful B 1 și B, A 1 iar A va coincide. Luați un cerc cu centrul A și raza AC și un al doilea cerc cu centrul B și raza BC. Aceste cercuri se vor intersecta în două puncte simetrice față de segmentul AB: punctul C și punctul C 2 . Aceasta înseamnă că C1, după mutarea triunghiului A1B1C1, trebuie să coincidă fie cu punctele C, fie cu C2. În orice caz, aceasta va însemna egalitatea △ABC=△A 1 B 1 C 1 , deoarece triunghiuri △ABC=△ABC 2 sunt egale (la urma urmei, aceste triunghiuri sunt simetrice față de segmentul AB.

Această proprietate – rigiditatea unui triunghi – este utilizată pe scară largă în practică. Așadar, pentru a securiza stâlpul în poziție verticală, se pune pe acesta un suport; același principiu este folosit la instalarea suportului.

Proprietatea rigidității triunghiului este utilizată pe scară largă în practică în construcția structurilor din fier.

Din al treilea criteriu pentru egalitatea triunghiurilor rezultă că un triunghi este o figură rigidă. Pentru că: ne putem imagina două șipci ale căror două capete sunt prinse cu un cui. Acest design nu este rigid, totuși, prin deplasarea sau răspândirea capetelor libere ale șipcilor, putem schimba unghiul dintre ele. Acum să luăm o altă șipcă și să-i fixăm capetele cu capetele libere ale primelor două șipci. Structura rezultată - un triunghi - va fi deja rigidă. Este imposibil să mutați sau să vă depărtați oricare două laturi, adică nici un colț nu poate fi schimbat. Într-adevăr, dacă acest lucru ar fi posibil, atunci am obține un nou triunghi, nu egal cu cel original. Dar acest lucru este imposibil, deoarece noul triunghi trebuie să fie egal cu cel original din al treilea

În cartea de referință despre matematica elementară de M. Ya Vygodsky, am găsit un alt semn.

Semnul Θ4: Dacă două laturi și unghiul opus celui mai mare al unui triunghi sunt, respectiv, egale cu două laturi și unghiul opus celui mai mare al altui triunghi, atunci astfel de triunghiuri sunt congruente.

Voi dovedi acest semn.

Dat : ΔABC, ΔA1B1C1, AB=A1B1,AC=A1C1,∠ B= ∠ B1

Demonstrați: ΔABC=A1B1C1.

Să aranjam triunghiurile ca în figura 1. Să conectăm B și B1, apoi ΔАВВ1

Isoscel înseamnă∠ 1= ∠ 2. ∠ 3= ∠ 4 ca resturi de unghiuri egale.

Obținem ΔВСВ1 - isoscel, deci ВС=В1С1. ΔАВС = ΔА1В1С1 pe trei laturi.

Tot în cursul școlar sunt discutate 4 semne de egalitate a triunghiurilor dreptunghiulare:

Θ1 . Dacă catetele unui triunghi dreptunghic sunt egale în mod corespunzător cu catetele altuia, atunci astfel de triunghiuri sunt congruente.

Θ2 . Dacă cateta și unghiul ascuțit adiacent al unui triunghi dreptunghic sunt, respectiv, egale cu cateta și unghiul ascuțit adiacent al altuia, atunci astfel de triunghiuri sunt congruente.

Θ3 . Dacă ipotenuza și unghiul ascuțit al unui triunghi dreptunghic sunt, respectiv, egale cu ipotenuza și unghiul ascuțit al altuia, atunci astfel de triunghiuri sunt congruente.

Θ4 . Dacă ipotenuza și catetul unui triunghi dreptunghic sunt, respectiv, egale cu ipotenuza și catetul altuia, atunci astfel de triunghiuri sunt congruente.

Am rezolvat baza teoretică pentru criteriile de egalitate a triunghiurilor, adăugând alte componente la laturile și unghiurile utilizate în testele clasice pentru egalitatea triunghiurilor: bisectoare, mediană și înălțime.

Criterii non-standard pentru congruența triunghiurilor.

1) Pe două laturi și înălțimea trasă pe una dintre ele.

Dat: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔABK=ΔA1B1K1 prin ipotenuză și catete, atunci∠ B= ∠ B1 și obțineți ΔABC= ΔA1B1C1 conform primului semn.

2) Pe două laturi și o mediană trasă la una dintre ele

Având în vedere: AB=A1B1, BC=B1C1, AK=A1K1, AK și A1K1 sunt mediane.

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔABK=ΔA1B1K1 pe trei laturi, ceea ce înseamnă∠ B= ∠ B1 și ΔABC= ΔA1B1C1 conform primului semn.

3) De-a lungul a două laturi și o înălțime trasă din al treilea colț.

Dat fiind: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔABK=ΔA1B1K1 de-a lungul piciorului și unghiului ascuțit, ceea ce înseamnă BK=B1K1,

ΔACK=ΔA1C1K1 prin catenă și unghi ascuțit, ceea ce înseamnă KC=K1C1 și, prin urmare, BC=B1C1, și ΔABC= ΔA1B1C1 prin al doilea semn.

4) De-a lungul unei laturi și două înălțimi trasate din unghiurile adiacente acestei laturi.

Dat: AC=A1C1, SM=C1M1, AK=A1K1.

Demonstrați: ΔСC= ΔA1B1C1.

Dovada: ΔAMC= ΔA1М1C1 de-a lungul catetei și ipotenuzei, ceea ce înseamnă∠ A= ∠ A1 și ΔAКC= ΔA1К1C1 de-a lungul catetei și ipotenuzei, ceea ce înseamnă∠ C= ∠ C1.

Deci, ΔABC= ΔA1B1C1 conform celui de-al doilea criteriu.

5) Pe două laturi și înălțimea trasă pe a treia latură.

Dat: AB=A1B1,BC=B1C1,BK=B1K1.

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔABK=ΔA1B1K1 pe ipotenuză și catete, ceea ce înseamnă AK=A1K1,

ΔBКC= ΔB1К1C1 de-a lungul catetei și ipotenuzei, ceea ce înseamnă KC=K1C1.

Deci, ΔABC= ΔA1B1C1 pe trei laturi.

6) De-a lungul laturii, unul dintre unghiurile adiacente acestei laturi și bisectoarea din acest unghi.

Dat: AC=A1C1, AK=A1K1,∠ A ∠ A1.

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔКАС=ΔК1А1С1 conform primului semn, ceea ce înseamnă∠ C= ∠ C1,

ΔABC= ΔA1B1C1 conform celei de-a doua caracteristici.

7) După două înălțimi și unghiul din care se trasează una dintre înălțimi.

Dat: SM=S1M1, AK=A1K1, ∠ A ∠ A1.

Demonstrați: ΔABC= ΔA1B1C1.

Dovada: ΔAMC= ΔA1М1C1 pe picior și unghi ascuțit, ΔКАС=ΔК1А1С1 pe picior și ipotenuză, ΔABC= ΔA1B1C1 pe al doilea semn.

Concluzie.

În timpul cercetării, am aflat că, pe lângă cele trei semne principale ale egalității triunghiurilor, se pot indica și multe altele. Am formulat și demonstrat egalitatea triunghiurilor pe baza medianei, altitudinii, bisectoarei triunghiului în combinație cu laturile și unghiurile triunghiului, aderând la prezența a trei elemente. Acum le pot spune elevilor școlii noastre că există și alte semne că triunghiurile sunt egale. Acest lucru va permite absolvenților școlii să aplice rezultatele cercetării mele în pregătirea pentru examenul de stat unificat și examenul de stat unificat și să rezolve cu ușurință probleme geometrice folosind aceste caracteristici.

Rezultatul cercetării mele: Au fost dovedite mai multe criterii de egalitate a triunghiurilor care nu sunt studiate la cursul de geometrie a școlii.

Bibliografie

1. Vygodsky M.Ya. Manual de matematică elementară.
2. Geometrie. Clasele 7-9: manual. Pentru invatamantul general instituții/L.S.Atanasyan, V.F.Butuzov, S.B. Kadomtsev și colab. – ed. a 19-a. – M.: Educație, 2009.
3. Pogorelov A.V Geometrie: manual. Pentru clasele 7-9. educatie generala Instituţiile. – ediția a 3-a. – M.: Educație, 2002.
4. . Enciclopedia „Avanta” în matematică, Moscova, 2004.
5. 2. Wikipedia este o enciclopedie liberă.
6. 3. Glazer G.I. „Istoria matematicii la școală”, Moscova, Prosveshchenie, 1982.
7. 4. Guseva T.M. Semne de similitudine ale triunghiurilor - Moscova, primul septembrie, supliment „Matematică”, 1999, nr. 28
8. 5. Pogorelov A.V. „Clasele de geometrie 7-9”Moscova, Educație, 2003

Anexa 1

1. Câte semne crezi că triunghiurile sunt egale?

A) 3 B) mai mult de trei C) mai puțin de trei

2. Ați dori să învățați semne noi pentru congruența triunghiurilor?

A) da B) nu

Se spune că două triunghiuri sunt congruente dacă pot fi reunite prin suprapunere. Figura 1 prezintă triunghiuri egale ABC și A 1 B 1 C 1. Fiecare dintre aceste triunghiuri poate fi suprapus peste celălalt, astfel încât să fie complet compatibile, adică vârfurile și laturile lor se potrivesc în perechi. Este clar că unghiurile acestor triunghiuri se vor potrivi și în perechi.

Astfel, dacă două triunghiuri sunt congruente, atunci elementele (adică laturile și unghiurile) unui triunghi sunt, respectiv, egale cu elementele celuilalt triunghi. Rețineți că în triunghiuri egale împotriva laturilor egale corespunzător(adică suprapunerea atunci când este suprapusă) unghiuri egale se află si inapoi: Laturile egale sunt opuse, respectiv unghiuri egale.

Deci, de exemplu, în triunghiuri egale ABC și A 1 B 1 C 1, prezentate în figura 1, laturile egale opuse AB și, respectiv, A 1 B 1, se află unghiuri egale C și C 1. Vom nota egalitatea triunghiurilor ABC și A 1 B 1 C 1 astfel: Δ ABC = Δ A 1 B 1 C 1. Rezultă că egalitatea a două triunghiuri poate fi stabilită prin compararea unora dintre elementele lor.

Teorema 1. Primul semn al egalității triunghiurilor. Dacă două laturi și unghiul dintre ele ale unui triunghi sunt, respectiv, egale cu două laturi și unghiul dintre ele ale altui triunghi, atunci astfel de triunghiuri sunt congruente (Fig. 2).

Dovada. Luați în considerare triunghiurile ABC și A 1 B 1 C 1, în care AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (vezi Fig. 2). Să demonstrăm că Δ ABC = Δ A 1 B 1 C 1 .

Deoarece ∠ A = ∠ A 1, atunci triunghiul ABC poate fi suprapus pe triunghiul A 1 B 1 C 1 astfel încât vârful A să fie aliniat cu vârful A 1, iar laturile AB și AC sunt suprapuse razelor A 1 B 1 și A 1. C 1 . Deoarece AB = A 1 B 1, AC = A 1 C 1, atunci latura AB se va alinia cu latura A 1 B 1 și latura AC se va alinia cu latura A 1 C 1; în special, punctele B și B 1, C și C 1 vor coincide. În consecință, laturile BC și B 1 C 1 vor coincide. Deci, triunghiurile ABC și A 1 B 1 C 1 sunt complet compatibile, ceea ce înseamnă că sunt egale.

Teorema 2 este demonstrată în mod similar folosind metoda suprapunerii.

Teorema 2. Al doilea semn al egalității triunghiurilor. Dacă o latură și două unghiuri adiacente ale unui triunghi sunt egale cu latura și, respectiv, două unghiuri adiacente ale altui triunghi, atunci astfel de triunghiuri sunt congruente (Fig. 34).

Cometariu. Pe baza teoremei 2, se stabilește teorema 3.

Teorema 3. Suma oricăror două unghiuri interioare ale unui triunghi este mai mică de 180°.

Teorema 4 rezultă din ultima teoremă.

Teorema 4. Un unghi exterior al unui triunghi este mai mare decât orice unghi interior care nu este adiacent acestuia.

Teorema 5. Al treilea semn al egalității triunghiurilor. Dacă trei laturi ale unui triunghi sunt, respectiv, egale cu trei laturi ale altui triunghi, atunci astfel de triunghiuri sunt congruente ().

Exemplul 1.În triunghiuri ABC și DEF (Fig. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm Comparați triunghiurile ABC și DEF. Ce unghi din triunghiul DEF este egal cu unghiul B?

Soluţie. Aceste triunghiuri sunt egale conform primului semn. Unghiul F al triunghiului DEF este egal cu unghiul B al triunghiului ABC, deoarece aceste unghiuri sunt opuse, respectiv, laturile egale DE și AC.

Exemplul 2. Segmentele AB și CD (Fig. 5) se intersectează în punctul O, care este mijlocul fiecăruia dintre ele. Care este lungimea segmentului BD dacă segmentul AC are 6 m?

Soluţie. Triunghiurile AOC și BOD sunt egale (după primul criteriu): ∠ AOC = ∠ BOD (vertical), AO = OB, CO = OD (după condiție).
Din egalitatea acestor triunghiuri rezultă că laturile lor sunt egale, adică AC = BD. Dar deoarece conform condiției AC = 6 m, atunci BD = 6 m.