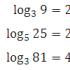Приклади з логарифмами та їх вирішення еге. Розв'язання логарифмічок рівнянь

Що таке логарифм?

Увага!
До цієї теми є додаткові
матеріали у Особливому розділі 555.
Для тих, хто сильно "не дуже..."
І для тих, хто "дуже навіть...")

Що таке логарифм? Як вирішувати логарифми? Ці питання багатьох випускників вводять у ступор. Традиційно тема логарифмів вважається складною, незрозумілою та страшною. Особливо – рівняння з логарифмами.

Це зовсім не так. Абсолютно! Не вірите? Добре. Зараз, за ​​якісь 10 – 20 хвилин ви:

1. Зрозумієте, що таке логарифм.

2. Навчіться розв'язувати цілий клас показових рівнянь. Навіть якщо про них нічого не чули.

3. Навчіться обчислювати прості логарифми.

Причому для цього вам потрібно буде знати лише таблицю множення, та як зводиться число до ступеня.

Відчуваю, сумніваєтеся ви... Ну гаразд, засікайте час! Поїхали!

Для початку вирішіть в умі ось таке рівняння:

Якщо Вам подобається цей сайт...

До речі, у мене є ще кілька цікавих сайтів для Вас.)

Можна потренуватися у вирішенні прикладів та дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося – з інтересом!)

можна познайомитися з функціями та похідними.

Дотримання Вашої конфіденційності є важливим для нас. З цієї причини ми розробили Політику Конфіденційності, яка описує, як ми використовуємо та зберігаємо Вашу інформацію. Будь ласка, ознайомтесь з нашими правилами дотримання конфіденційності та повідомте нам, якщо у вас виникнуть будь-які питання.

Збір та використання персональної інформації

Під персональної інформацією розуміються дані, які можна використовувати для ідентифікації певного особи чи зв'язку з ним.

Від вас може бути запитане надання вашої персональної інформації будь-коли, коли ви зв'язуєтеся з нами.

Нижче наведено деякі приклади типів персональної інформації, яку ми можемо збирати, і як ми можемо використовувати таку інформацію.

Яку персональну інформацію ми збираємо:

• Коли ви залишаєте заявку на сайті, ми можемо збирати різноманітну інформацію, включаючи ваше ім'я, номер телефону, адресу електронної пошти тощо.

Як ми використовуємо вашу персональну інформацію:

• Персональна інформація, що збирається нами, дозволяє нам зв'язуватися з вами та повідомляти про унікальні пропозиції, акції та інші заходи та найближчі події.
• Час від часу ми можемо використовувати вашу персональну інформацію для надсилання важливих повідомлень та повідомлень.
• Ми також можемо використовувати персональну інформацію для внутрішніх цілей, таких як проведення аудиту, аналізу даних та різних досліджень з метою покращення послуг, що надаються, та надання Вам рекомендацій щодо наших послуг.
• Якщо ви берете участь у розіграші призів, конкурсі або подібному стимулювальному заході, ми можемо використовувати інформацію, що надається, для управління такими програмами.

Розкриття інформації третім особам

Ми не розкриваємо отриману від Вас інформацію третім особам.

Винятки:

• Якщо необхідно - відповідно до закону, судовим порядком, у судовому розгляді, та/або на підставі публічних запитів або запитів від державних органів на території РФ - розкрити вашу персональну інформацію. Ми також можемо розкривати інформацію про вас, якщо ми визначимо, що таке розкриття необхідно або доречно з метою безпеки, підтримання правопорядку, або інших суспільно важливих випадків.
• У разі реорганізації, злиття або продажу ми можемо передати персональну інформацію, що збирається нами, відповідній третій особі – правонаступнику.

Захист персональної інформації

Ми вживаємо запобіжних заходів - включаючи адміністративні, технічні та фізичні - для захисту вашої персональної інформації від втрати, крадіжки та недобросовісного використання, а також від несанкціонованого доступу, розкриття, зміни та знищення.

Дотримання вашої конфіденційності на рівні компанії

Для того, щоб переконатися, що ваша персональна інформація знаходиться в безпеці, ми доводимо норми дотримання конфіденційності та безпеки до наших співробітників, і суворо стежимо за виконанням заходів дотримання конфіденційності.

Логарифмічні вирази, розв'язання прикладів. У цій статті ми розглянемо завдання, пов'язані з вирішенням логарифмів. У завданнях порушується питання про знаходження значення висловлювання. Потрібно відзначити, що поняття логарифма використовується в багатьох завданнях і розуміти його сенс дуже важливо. Що ж до ЄДІ, то логарифм використовується під час вирішення рівнянь, у прикладних завданнях, і навіть у завданнях що з дослідженням функцій.

Наведемо приклади для розуміння самого сенсу логарифму:

Основне логарифмічне тотожність:

Властивості логарифмів, які необхідно завжди пам'ятати:

*Логарифм твору дорівнює сумі логарифмів співмножників.

* * *

*Логарифм приватного (дробу) дорівнює різниці логарифмів співмножників.

* * *

*Логарифм ступеня дорівнює добутку показника ступеня на логарифм його заснування.

* * *

*Перехід до нової основи

* * *

Ще властивості:

* * *

Обчислення логарифмів тісно пов'язане з використанням властивостей показників ступеня.

Перерахуємо деякі з них:

Суть цієї властивості полягає в тому, що при перенесенні чисельника у знаменник і навпаки, знак показника ступеня змінюється на протилежний. Наприклад:

Наслідок з цієї властивості:

* * *

При зведенні ступеня в ступінь основа залишається такою, а показники перемножуються.

* * *

Як ви переконалися саме поняття логарифму нескладне. Головне те, що потрібна хороша практика, яка дає певну навичку. Вочевидь знання формул обов'язково. Якщо навичка у перетворенні елементарних логарифмів не сформована, то при вирішенні простих завдань можна легко припуститися помилки.

Практикуйтесь, вирішуйте спочатку найпростіші приклади з курсу математики, потім переходьте до складніших. У майбутньому обов'язково покажу, як вирішуються «страшненькі» логарифми, таких на ЄДІ не буде, але вони цікаві, не пропустіть!

На цьому все! Успіху Вам!

З повагою, Олександр Крутицьких

PS: Буду вдячний Вам, якщо розповісте про сайт у соціальних мережах.

У цьому відеоуроці ми розглянемо рішення досить серйозного логарифмічного рівняння, в якому не просто потрібно знайти коріння, а й відібрати ті, які лежать на заданому відрізку.

Завдання C1. Розв'яжіть рівняння. Знайдіть усі корені цього рівняння, що належать до проміжку.

Зауваження щодо логарифмічних рівнянь

Однак з року в рік до мене приходять учні, які намагаються вирішувати ось такі, прямо скажемо, непрості рівнянняАле при цьому не можуть зрозуміти: з чого їм взагалі починати і як підступитися до логарифмів? Така проблема може виникнути навіть у сильних, добре підготовлених учнів.

В результаті багато хто починає боятися цієї теми, а то й взагалі вважати себе тупими. Так ось, запам'ятайте: якщо у вас не виходить вирішити таке рівняння, це зовсім не означає, що ви тупі. Тому що, наприклад, ось з таким рівнянням ви справитеся практично усно:

log 2 x = 4

А якщо це не так, ви зараз не читали б цей текст, оскільки були зайняті більш простими та приземленими завданнями. Звичайно, хтось зараз заперечить: «А яке відношення це найпростіше рівняння має до нашої здорової конструкції?» Відповідаю: будь-яке логарифмічне рівняння, яким би складним воно не було, у результаті зводиться ось до таких найпростіших конструкцій, що усно вирішуються.

Зрозуміло, переходити від складних логарифмічних рівнянь до більш простих потрібно не за допомогою підбору або танців з бубном, а за чіткими, давно визначеними правилами, які так і називаються. правила перетворення логарифмічних виразів. Знаючи їх, ви легко розберетеся навіть з навороченими рівняннями в ЄДІ з математики.

І саме про ці правила ми говоритимемо у сьогоднішньому уроці. Поїхали!

Розв'язання логарифмічного рівняння задачі C1

Отже, вирішуємо рівняння:

Насамперед, коли йдеться про логарифмічні рівняння, згадуємо основну тактику — якщо можна сказати, основне правило розв'язання логарифмічних рівнянь. Полягає воно в наступному:

Теорема про канонічну форму. Будь-яке логарифмічне рівняння, що б у нього не входило, які б логарифми, з якої б підстави, і що б у собі не отримали, обов'язково потрібно привести до рівняння виду:

log a f (x) = log a g (x)

Якщо ми подивимося на наше рівняння, то зауважимо одразу дві проблеми:

1. Зліва у нас стоїть сума двох чисел, одна з яких взагалі не є логарифмом.
2. Справа стоїть цілком собі логарифм, однак у його підставі стоїть корінь. А у логарифму ліворуч – просто 2, тобто. Основи логарифмів ліворуч і праворуч різняться.

Отже, ми склали такий перелік проблем, які відокремлюють наше рівняння від того канонічного рівняння, якого потрібно привести будь-яке логарифмічне рівняння у процесі решения. Таким чином, рішення нашого рівняння на цьому етапі зводиться до того, щоб усунути описані вище дві проблеми.

Будь-яке логарифмічне рівняння вирішується швидко та легко, якщо звести його до канонічної форми.

Сума логарифмів та логарифм твору

Давайте діяти по порядку. Спочатку розберемося з конструкцією, що стоїть ліворуч. Що ми можемо сказати про суму двох логарифмів? Давайте згадаємо чудову формулу:

log a f (x) + log a g (x) = log a f (x) · g (x)

Але варто врахувати, що в нашому випадку перший доданок взагалі не є логарифмом. Отже, потрібно уявити одиницю як логарифму з підстави 2 (саме 2, оскільки ліворуч стоїть логарифм з підстави 2). Як це зробити? Знову згадуємо чудову формулу:

a = log b b a

Тут треба розуміти: коли ми говоримо «Будь-яка основа b», то маємо на увазі, що b все-таки не може бути довільним числом. Якщо ми вставляємо якесь число в логарифм, на нього одразу накладаються певні обмеження, А саме: підстава логарифму має бути більше 0 і не повинно бути рівним 1. Інакше логарифм просто не має сенсу. Запишемо це:

0 < b ≠ 1

Давайте подивимося, що відбувається у нашому випадку:

1 = log 2 2 1 = log 2 2

Тепер перепишемо наше рівняння з урахуванням цього факту. І відразу ж застосовуємо інше правило: сума логарифмів дорівнює логарифму добутку аргументів. У результаті отримаємо:

Ми здобули нове рівняння. Як бачимо, воно вже набагато ближче до того канонічного рівняння, якого ми прагнемо. Але є одна проблема, ми записали її у вигляді другого пункту: у наших логарифмів, які стоять ліворуч і праворуч, різні підстави. Переходимо до наступного кроку.

Правила винесення ступенів із логарифму

Отже у логарифму, який стоїть ліворуч, основа просто 2, а у логарифму, який стоїть праворуч, в основі є корінь. Але це не є проблемою, якщо згадати, що з підстав з аргументів логарифму можна виносити в ступінь. Давайте запишемо одне з цих правил:

log a b n = n · log a b

Переклавши на людську мову: можна виносити ступінь з основи логарифму і ставити її спереду як множник. Число n «мігрувало» з логарифму назовні і стало коефіцієнтом спереду.

З тим самим успіхом ми можемо винести ступінь із основи логарифму. Виглядатиме це так:

Іншими словами, якщо винести ступінь з аргументу логарифму, цей ступінь також пишеться як множник перед логарифмом, але вже не у вигляді числа, а у вигляді зворотного числа 1/k.

Проте це ще не все! Ми можемо об'єднати дві дані формули і почитати таку формулу:

Коли ступінь стоїть і в підставі, і в аргументі логарифму, ми можемо заощадити час і спростити обчислення, якщо одразу винести ступінь і з основи, і з аргументу. При цьому те, що стояло в аргументі (у нашому випадку це коефіцієнт n), опиниться в чисельнику. А те, що було ступенем біля основи, a k , вирушить у знаменник.

І саме ці формули ми зараз будемо застосовувати для того, щоб звести наші логарифми до однієї й тієї самої основи.

Насамперед, виберемо більш-менш красиву основу. Очевидно, що з двійкою в основі набагато приємніше працювати, ніж із коренем. Таким чином, давайте спробуємо привести другий логарифм до основи 2. Давайте випишемо цей логарифм окремо:

Що ми можемо зробити тут? Згадаймо формулу ступеня із раціональним показником. Іншими словами, ми можемо записати в корені як ступінь з раціональним показником. А потім виносимо ступінь 1/2 і з аргументу, і з основи логарифму. Скорочуємо двійки в коефіцієнтах у чисельнику та знаменнику, що стоять перед логарифмом:

Нарешті, перепишемо вихідне рівняння з урахуванням нових коефіцієнтів:

log 2 2(9x 2 + 5) = log 2 (8x 4 + 14)

Ми здобули канонічне логарифмічне рівняння. І ліворуч, і праворуч у нас стоїть логарифм по тому самому підставі 2. Крім цих логарифмів ніяких коефіцієнтів, ніяких доданків ні ліворуч, ні праворуч немає.

Отже, ми можемо позбутися знаку логарифму. Зрозуміло, з урахуванням області визначення. Але перш ніж це зробити, давайте повернемося назад і зробимо невелике уточнення з приводу дробів.

Поділ дробу на дріб: додаткові міркування

Далеко не всім учням зрозуміло, звідки беруться і куди подіться множники перед правим логарифмом. Запишемо ще раз:

Давайте розберемося, що таке дріб. Запишемо:

А тепер згадуємо правило поділу дробів: щоб поділити на 1/2 потрібно помножити на перевернутий дріб:

Зрозуміло, для зручності подальших обчислень ми можемо записати двійку як 2/1 — і це ми спостерігаємо як другий коефіцієнт у процесі рішення.

Сподіваюся тепер усім зрозуміло, звідки береться другий коефіцієнт, тому переходимо безпосередньо до вирішення нашого канонічного логарифмічного рівняння.

Звільнення від знаку логарифму

Нагадую, що зараз ми можемо позбавитися логарифмів і залишити наступний вираз:

2(9x2+5) = 8x4+14

Давайте розкриємо дужки зліва. Отримаємо:

18x2+10 = 8x4+14

Перенесемо все з лівої частини до правої:

8x 4 + 14 − 18x 2 − 10 = 0

Наведемо подібні та отримаємо:

8x 4 − 18x 2 + 4 = 0

Можемо розділити обидві частини цього рівняння на 2, щоб спростити коефіцієнти і отримаємо:

4x 4 − 9x 2 + 2 = 0

Перед нами звичайне біквадратне рівняння, і його коріння легко вважаються через дискримінант. Отже, запишемо дискримінант:

D = 81 − 4 · 4 · 2 = 81 − 32 = 49

Прекрасно, Дискримінант «красивий», корінь з нього дорівнює 7. Все, вважаємо самі ікси. Але в даному випадку коріння виходить не x, а x2, тому що у нас біквадратне рівняння. Отже, наші варіанти:

Зверніть увагу: ми витягували коріння, тому відповіді будуть дві, т.к. квадрат - функція парна. І якщо ми напишемо лише корінь із двох, то другий корінь ми просто втратимо.

Тепер розписуємо другий корінь нашого біквадратного рівняння:

Знову ж таки, ми отримуємо арифметичний квадратний корінь з обох частин нашого рівняння та отримуємо два корені. Однак пам'ятайте:

Недостатньо просто прирівняти аргументи логарифмів у канонічній формі. Пам'ятайте про область визначення!

Разом ми отримали чотири корені. Усі вони є рішеннями нашого вихідного рівняння. Погляньте: у нашому вихідному логарифмічному рівнянні всередині логарифмів стоїть або 9x2+5 (ця функція завжди позитивна), або 8x4+14 - вона теж завжди позитивна. Отже, область визначення логарифмів виконується у будь-якому разі, який би корінь ми не отримали, а це означає, що всі чотири корені є рішеннями нашого рівняння.

Прекрасно, тепер переходимо до другої частини завдання.

Відбір коренів логарифмічного рівняння на відрізку

Відбираємо з наших чотирьох коренів ті, що лежать на відрізку [−1; 8/9]. Повертаємося до нашого коріння, і зараз виконуватимемо їх відбір. Для початку пропоную накреслити координатну вісь та відзначити на ній кінці відрізка:

Обидві точки будуть зафарбовані. Тобто. за умовою завдання нас цікавить заштрихований відрізок. Тепер давайте розбиратися з корінням.

Ірраціональне коріння

Почнемо з ірраціонального коріння. Зауважимо, що 8/9< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

З цього випливає, що корінь із двох не потрапляє в цікавий для нас відрізок. Аналогічно ми отримаємо і з негативним коренем: він менше, ніж −1, тобто лежить лівіше відрізка, що цікавить нас.

Раціональне коріння

Залишається два корені: x = 1/2 та x = −1/2. Зауважимо, що лівий кінець відрізка (−1) – негативний, а правий (8/9) – позитивний. Отже, десь між цими кінцями лежить число 0. Корінь x = −1/2 буде між −1 і 0, тобто. потрапить у остаточну відповідь. Аналогічно чинимо з коренем x = 1/2. Цей корінь також лежить на відрізку, що розглядається.

Переконатися, що число 8/9 більше ніж 1/2, можна дуже просто. Давайте віднімемо ці числа одне з одного:

Отримали дріб 7/18 > 0, але це за визначенням означає, що 8/9 > 1/2.

Давайте відзначимо відповідне коріння на осі координат:

Остаточною відповіддю будуть два корені: 1/2 та −1/2.

Порівняння ірраціональних чисел: універсальний алгоритм

На закінчення хотів би ще раз повернутися до ірраціональних чисел. На прикладі ми зараз подивимося, як порівнювати раціональні і ірраціональні величини в математиці. Для початку між ними таку галочку V — знак «більше» або «менше», але ми поки що не знаємо, в який бік він спрямований. Запишемо:

Навіщо взагалі потрібні якісь алгоритми порівняння? Справа в тому, що в цьому завданні нам дуже пощастило: у процесі вирішення виникло розділяюче число 1, про яке ми можемо точно сказати:

Однак далеко не завжди ви відразу побачите таке число. Тому давайте спробуємо порівняти наші числа "в лоб", безпосередньо.

Як це робиться? Робимо те саме, що і зі звичайними нерівностями:

1. Спочатку, якби в нас десь були негативні коефіцієнти, ми помножили б обидві частини нерівності на −1. Зрозуміло, помінявши при цьому знак. Отака галочка V змінилася б на таку — Λ.
2. Але в нашому випадку обидві сторони вже позитивні, тому нічого не треба міняти. Що дійсно потрібно, то це звести обидві частини квадрат, щоб позбавитися радикала.

Якщо при порівнянні ірраціональних чисел не вдається з ходу підібрати елемент, що розділяє, рекомендую виконувати таке порівняння «в лоб» — розписуючи як звичайна нерівність.

При вирішенні це оформляється таким чином:

Тепер все це легко порівнюється. Справа в тому, що 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

Все, ми отримали суворий доказ, що всі числа відзначені на числовий прямий х правильно і саме в тій послідовності, в якій вони мають бути насправді. Ось до такого рішення ніхто не причепиться, тому запам'ятайте: якщо ви відразу не бачите розділяюче число (у нашому випадку це 1), то сміливо виписуйте наведену вище конструкцію, множте, зводьте в квадрат - і в результаті ви отримаєте гарну нерівність. З цієї нерівності точно буде зрозуміло, яке число більше, а яке менше.

Повертаючись до нашого завдання, хотілося б ще раз звернути увагу на те, що ми робили на самому початку при вирішенні нашого рівняння. А саме: ми уважно подивилися на наше вихідне логарифмічне рівняння та спробували звести його до канонічномулогарифмічного рівняння. Де ліворуч і праворуч стоять лише логарифми - без будь-яких додаткових доданків, коефіцієнтів спереду і т. д. Нам потрібні не два логарифми на підставі a або b, саме логарифм, що дорівнює іншому логарифму.

Крім того, підстави логарифмів також мають бути рівними. При цьому якщо рівняння складено грамотно, то за допомогою елементарних логарифмічних перетворень (сума логарифмів, перетворення числа на логарифм тощо) ми зведемо це рівняння саме до канонічного.

Тому надалі, коли ви бачите логарифмічне рівняння, яке не вирішується одразу «в лоб», не варто губитися або намагатися підібрати відповідь. Достатньо виконати такі кроки:

1. Привести усі вільні елементи до логарифму;
2. Потім ці логарифми скласти;
3. В отриманій конструкції всі логарифми призвести до однієї й тієї самої основи.

В результаті ви отримаєте просте рівняння, яке вирішується елементарними засобами алгебри із матеріалів 8-9 класу. Загалом, заходьте на мій сайт, тренуйтеся вирішувати логарифми, вирішуйте логарифмічні рівняння як я, вирішуйте їх краще за мене. А я на цьому все. З Вами був Павло Бердов. До нових зустрічей!

Як відомо, при перемноженні виразів зі ступенями їх показники завжди складаються (a b * a c = a b + c). Цей математичний закон був виведений Архімедом, а згодом, у VIII столітті, математик Вірасен створив таблицю цілих показників. Саме вони стали для подальшого відкриття логарифмів. Приклади використання цієї функції можна зустріти практично скрізь, де потрібно спростити громіздке множення на просте додавання. Якщо ви витратите 10 хвилин на прочитання цієї статті, ми вам пояснимо, що таке логарифми і як з ними працювати. Простим та доступним мовою.

Визначення у математиці

Логарифмом називається вираз наступного виду: log ab=c, тобто логарифмом будь-якого неотрицательного числа (тобто будь-якого позитивного) "b" на його підставі "a" вважається ступінь "c", в яку необхідно звести підставу "a", щоб у результаті отримати значення "b". Розберемо логарифм на прикладах, скажімо, є вираз log 2 8. Як знайти відповідь? Дуже просто, потрібно знайти такий ступінь, щоб з 2 до ступеня отримати 8. Зробивши в умі деякі розрахунки, отримуємо число 3! І вірно, адже 2 в ступені 3 відповідає у відповідь число 8.

Різновиди логарифмів

Для багатьох учнів і студентів ця тема здається складною і незрозумілою, проте насправді логарифми не такі страшні, головне - зрозуміти загальний їхній сенс і запам'ятати їх свійста і деякі правила. Існує три окремі види логарифмічних виразів:

1. Натуральний логарифм ln a де основою є число Ейлера (e = 2,7).
2. Десятковий a де підставою служить число 10.
3. Логарифм будь-якого числа b на підставі a>1.

Кожен з них вирішується стандартним способом, що включає спрощення, скорочення і подальше приведення до одного логарифму за допомогою логарифмічних теорем. Для отримання вірних значень логарифмів слід запам'ятати їх властивості та черговість дій у разі їх вирішення.

Правила та деякі обмеження

У математиці існує кілька правил-обмежень, які приймаються як аксіома, тобто не підлягають обговоренню та є істиною. Наприклад, не можна числа ділити на нуль, а ще неможливо витягти корінь парного ступеня з негативних чисел. Логарифми також мають свої правила, дотримуючись яких можна легко навчитися працювати навіть з довгими і ємними логарифмічними виразами:

• основа "a" завжди має бути більшою за нуль, і при цьому не бути рівним 1, інакше вираз втратить свій сенс, адже "1" і "0" у будь-якій мірі завжди рівні своїм значенням;
• якщо а > 0, то і а >0, виходить, що і "з" має бути більше нуля.

Як вирішувати логарифми?

Наприклад, дано завдання знайти відповідь рівняння 10 х = 100. Це дуже легко, потрібно підібрати таку міру, звівши в яку число десять, ми отримаємо 100. Це, звичайно, 10 2 =100.

А тепер давайте уявимо цей вираз у вигляді логарифмічного. Отримаємо log 10 100 = 2. При вирішенні логарифмів всі дії практично сходяться до того, щоб знайти той ступінь, в який необхідно ввести основу логарифму, щоб отримати задане число.

Для безпомилкового визначення значення невідомого ступеня необхідно навчитися працювати з таблицею ступенів. Виглядає вона так:

Як бачите, деякі показники ступеня можна вгадати інтуїтивно, якщо є технічний склад розуму та знання таблиці множення. Однак для великих значень знадобиться таблиця ступенів. Нею можуть користуватися навіть ті, хто зовсім нічого не тямить у складних математичних темах. У лівому стовпці вказані числа (основа a), верхній ряд чисел - це значення ступеня c, у якому зводиться число a. На перетині в осередках визначено значення чисел, що є відповіддю (a c = b). Візьмемо, наприклад, найпершу комірку з числом 10 і зведемо її в квадрат, отримаємо значення 100, яке зазначено на перетині двох наших осередків. Все так просто і легко, що зрозуміє навіть справжнісінький гуманітарій!

Рівняння та нерівності

Виходить, що за певних умов показник ступеня – це і є логарифм. Отже, будь-які математичні чисельні вирази можна записати як логарифмічного рівності. Наприклад, 3 4 =81 можна записати у вигляді логарифму числа 81 на підставі 3, що дорівнює чотирьом (log 3 81 = 4). Для негативних ступенів правила такі самі: 2 -5 = 1/32 запишемо у вигляді логарифму, отримаємо log 2 (1/32) = -5. Однією з найцікавіших розділів математики є тема "Логарифми". Приклади та розв'язання рівнянь ми розглянемо трохи нижче, відразу після вивчення їх властивостей. А зараз давайте розберемо, як виглядають нерівності та як їх відрізнити від рівнянь.

Дано вираз наступного виду: log 2 (x-1) > 3 - воно є логарифмічною нерівністю, тому що невідоме значення "х" знаходиться під знаком логарифму. А також у виразі порівнюються дві величини: логарифм шуканого числа на підставі два більше, ніж число три.

Найголовніша відмінність між логарифмічними рівняннями та нерівностями полягає в тому, що рівняння з логарифмами (приклад - логарифм 2 x = √9) мають на увазі у відповіді одне або кілька певних числових значень, тоді як при розв'язанні нерівності визначаються як область допустимих значень, розрив цієї функції. Як наслідок, у відповіді виходить не проста безліч окремих чисел як у відповіді рівняння, а безперервний ряд або набір чисел.

Основні теореми про логарифми

При вирішенні примітивних завдань знаходження значень логарифма, його властивості можна і не знати. Однак коли мова заходить про логарифмічні рівняння або нерівності, в першу чергу необхідно чітко розуміти і застосовувати на практиці всі основні властивості логарифмів. З прикладами рівнянь ми познайомимося пізніше, давайте спочатку розберемо кожну властивість докладніше.

1. Основне тотожність має такий вигляд: а logaB =B. Воно застосовується лише за умови, коли а більше 0, не дорівнює одиниці і B більше за нуль.
2. Логарифм твору можна представити у такій формулі: log d(s 1 *s 2) = log d s 1 + log d s 2. При цьому обов'язковою умовою є: d, s 1 та s 2 > 0; а≠1. Можна навести доказ цієї формули логарифмів, з прикладами і рішенням. Нехай log as 1 = f 1 і log as 2 = f 2 тоді a f1 = s 1 , a f2 = s 2. Отримуємо, що s 1 *s 2 = a f1 *a f2 = a f1+f2 (властивості ступенів ), а далі за визначенням: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log as 2, що і потрібно довести.
3. Логарифм приватного виглядає так: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Теорема у вигляді формули набуває наступного вигляду: log a q b n = n/q log a b.

Називається ця формула "властивістю ступеня логарифму". Вона нагадує властивості звичайних ступенів, і не дивно, адже вся математика тримається на закономірних постулатах. Давайте подивимося на доказ.

Нехай log a b = t, виходить a t = b. Якщо звести обидві частини до ступеня m: a tn = b n ;

але оскільки a tn = (a q) nt/q = b n, отже log a q b n = (n * t) / t, тоді log a q b n = n / q log a b. Теорему доведено.

Приклади завдань та нерівностей

Найпоширеніші типи завдань на тему логарифмів – приклади рівнянь та нерівностей. Вони зустрічаються практично у всіх задачниках, а також входять до обов'язкової частини іспитів з математики. Для вступу до університету чи здачі вступних випробувань з математики необхідно знати, як правильно вирішувати подібні завдання.

На жаль, єдиного плану або схеми щодо вирішення та визначення невідомого значення логарифму не існує, однак до кожної математичної нерівності або логарифмічного рівняння можна застосувати певні правила. Насамперед слід з'ясувати, чи можна спростити вираз чи привести до загального вигляду. Спрощувати довгі логарифмічні вирази можна, якщо правильно використати їх властивості. Давайте швидше із ними познайомимося.

При вирішенні ж логарифмічних рівнянь слід визначити, який перед нами вид логарифму: приклад виразу може містити натуральний логарифм або десятковий.

Ось приклади ln100, ln1026. Їхнє рішення зводиться до того, що потрібно визначити той ступінь, в якому підстава 10 буде дорівнює 100 і 1026 відповідно. Для рішень натуральних логарифмів потрібно застосувати логарифмічні тотожності або їх властивості. Давайте на прикладах розглянемо розв'язання логарифмічних завдань різного типу.

Як використовувати формули логарифмів: з прикладами та рішеннями

Отже, розглянемо приклади використання основних теорем про логарифми.

1. Властивість логарифму твору можна застосовувати в завданнях, де необхідно розкласти велике значення числа на більш прості співмножники. Наприклад, log 2 4 + log 2128 = log 2 (4 * 128) = log 2512. Відповідь дорівнює 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - як бачите, застосовуючи четверту властивість ступеня логарифму, вдалося вирішити на перший погляд складний і невирішуваний вираз. Необхідно лише розкласти основу на множники і потім винести значення ступеня зі знака логарифму.

Завдання з ЄДІ

Логарифми часто зустрічаються на вступних іспитах, особливо багато логарифмічних завдань у ЄДІ (державний іспит для всіх випускників шкіл). Зазвичай ці завдання присутні у частині А (найлегша тестова частина іспиту), а й у частини З (найскладніші і об'ємні завдання). Іспит передбачає точне та ідеальне знання теми "Натуральні логарифми".

Приклади та розв'язання задач взяті з офіційних варіантів ЄДІ. Давайте подивимося, як вирішуються такі завдання.

Дано log 2 (2x-1) = 4. Рішення:
перепишемо вираз, трохи спростивши його log 2 (2x-1) = 2 2 , за визначенням логарифму отримаємо, що 2x-1 = 2 4 , отже 2x = 17; х = 8,5.

• Всі логарифми найкраще приводити до однієї основи, щоб рішення не було громіздким та заплутаним.
• Всі вирази, що стоять під знаком логарифму, вказуються як позитивні, тому при винесенні множником показника ступеня виразу, який стоїть під знаком логарифму і як його підстава, вираз, що залишається під логарифмом, має бути позитивним.