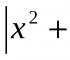Nejnovější příklady logaritmů aktivity. Logaritmy: příklady a řešení

Tento článek se zaměřuje na - logaritmus... Zde uvedeme definici logaritmu, ukážeme přijatou notaci, uvedeme příklady logaritmů a řekneme o přirozených a desetinných logaritmech. Poté zvažte základní logaritmickou identitu.

Navigace po stránce.

Definice logaritmu

Koncept logaritmu vzniká při řešení problému v určitém smyslu obráceně, když potřebujete najít exponenta se známou hodnotou stupně a známou základnou.

Ale dost předmluv, je čas odpovědět na otázku „co je to logaritmus“? Uveďme vhodnou definici.

Definice.

Logaritmická základna a z b, kde a> 0, a ≠ 1 a b> 0 je exponent, na který musí být zvýšeno číslo a, aby bylo výsledkem b.

V této fázi si všimneme, že mluvené slovo „logaritmus“ by mělo okamžitě vyvolat dvě výsledné otázky: „jaké číslo“ a „z jakého důvodu“. Jinými slovy, jednoduše neexistuje logaritmus, ale existuje pouze logaritmus čísla v nějaké základně.

Okamžitě vstoupit logaritmická notace: logaritmus čísla b k základu a se obvykle označuje jako log a b. Logaritmus čísla b k základně e a logaritmus k základně 10 mají svá vlastní speciální označení lnb a lgb, to znamená, že nepíšou log e b, ale lnb, a ne log 10 b, ale lgb.

Nyní můžete přinést:
A záznamy nedávají smysl, protože v prvním z nich pod znamením logaritmu je záporné číslo, ve druhém - záporné číslo na základně a ve třetím - oba záporné číslo pod znamením logaritmu a jeden na základně.

Nyní řekněme o pravidla pro čtení logaritmů... Log a b zní jako „logaritmus b k zakládání a“. Například log 2 3 je logaritmus tří základny 2 a je logaritmus dvou celých dvou třetin základny Odmocnina z pěti. Logaritmická základna e se nazývá přirozený logaritmus a lnb čte „přirozený logaritmus b“. Například ln7 je přirozený logaritmus sedmi a čteme jej jako přirozený logaritmus pí. Logaritmická základna 10 má také speciální název - dekadický logaritmus a položka lgb zní „log decimal b“. Například lg1 je desítkový logaritmus jedné a lg2.75 je desítkový logaritmus dvou bodů sedmdesát pět setin.

Stojí za to zabývat se samostatně za podmínek a> 0, a ≠ 1 a b> 0, za kterých je dána definice logaritmu. Vysvětlíme, odkud tato omezení pocházejí. K tomu nám pomůže rovnost volaného tvaru, která přímo vyplývá z výše uvedené definice logaritmu.

Začněme ≠ 1. Vzhledem k tomu, že jedna se rovná jedné jakékoli mocnině, může být rovnost platná pouze pro b = 1, ale log 1 1 může být jakékoli reálné číslo. Aby se předešlo této nejednoznačnosti, předpokládá se, že 1.

Zdůvodněme účelnost stavu a> 0. Pro a = 0 bychom podle definice logaritmu měli rovnost, která je možná pouze pro b = 0. Ale pak log 0 0 může být jakékoli nenulové reálné číslo, protože nula v jakémkoli nenulovém stupni je nula. Podmínka a ≠ 0 umožňuje vyhnout se této nejednoznačnosti. A pro<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Поэтому и принимается условие a>0 .

Konečně podmínka b> 0 vyplývá z nerovnosti a> 0, protože a hodnota stupně s kladnou základnou a je vždy kladná.

Na závěr tohoto odstavce říkáme, že vyjádřená definice logaritmu vám umožňuje okamžitě označit hodnotu logaritmu, když je číslo pod znaménkem logaritmu do určité míry základny. Definice logaritmu nám umožňuje tvrdit, že pokud b = a p, pak se logaritmus b základny a rovná p. To znamená, že protokol rovnosti a a p = p je pravdivý. Například víme, že 2 3 = 8, potom log 2 8 = 3. Více si o tom povíme v článku.

Dnes si povíme logaritmické vzorce a uvést orientační příklady řešení.

Sami o sobě naznačují rozhodovací šablony podle základních vlastností logaritmů. Před použitím vzorců logaritmů pro řešení si pro vás vybavíme nejprve všechny vlastnosti:

Nyní na základě těchto vzorců (vlastností) ukážeme příklady řešení logaritmů.

Příklady řešení logaritmů na základě vzorců.

Logaritmus kladné číslo b v základu a (označeno log a b) je exponent, na který musí být zvýšeno a, aby bylo získáno b, zatímco b> 0, a> 0 a 1.

Podle definice log a b = x, což je ekvivalentní a x = b, proto log a a x = x.

Logaritmy, příklady:

log 2 8 = 3, protože 2 3 = 8

log 7 49 = 2, protože 7 2 = 49

log 5 1/5 = -1, protože 5 -1 = 1/5

Desetinný logaritmus je obvyklý logaritmus, jehož základna je 10. Označuje se jako lg.

log 10 100 = 2, protože 10 2 = 100

Přirozený logaritmus- také obvyklý logaritmus je logaritmus, ale se základnou e (e = 2,71828 ... je iracionální číslo). Je označen jako ln.

Je vhodné si zapamatovat vzorce nebo vlastnosti logaritmů, protože je budeme v budoucnu potřebovat při řešení logaritmů, logaritmických rovnic a nerovnic. Zkusme každý vzorec ještě jednou s příklady.

Základní logaritmická identita
a log a b = b
8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9
Logaritmus produktu se rovná součtu logaritmů
log a (bc) = log a b + log a c
log 3 8.1 + log 3 10 = log 3 (8.1 * 10) = log 3 81 = 4
Logaritmus kvocientu se rovná rozdílu logaritmů
log a (b / c) = log a b - log a c
9 log 5 50/9 log 5 2 = 9 log 5 50-log 5 2 = 9 log 5 25 = 9 2 = 81
Vlastnosti síly logaritmu a báze logaritmu
Exponent logaritmu čísla log a b m = mlog a b

Exponent základny logaritmu log a n b = 1 / n * log a b

log a n b m = m / n * log a b,

pokud m = n, dostaneme log a n b n = log a b

log 4 9 = log 2 2 3 2 = log 2 3
Přechod k novému základu
log a b = log c b / log c a,
pokud c = b, dostaneme log b b = 1

pak log a b = 1 / log b a

log 0,8 3 * log 3 1,25 = log 0,8 3 * log 0,8 1,25 / log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Jak vidíte, vzorce pro logaritmy nejsou tak složité, jak se zdají. Po zvážení příkladů řešení logaritmů můžeme přejít k logaritmickým rovnicím. Podrobněji se budeme zabývat příklady řešení logaritmických rovnic v článku: „“. Nenechte si ujít!

Pokud máte ohledně řešení stále otázky, napište je do komentářů k článku.

Poznámka: rozhodli jsme se získat vzdělání v jiné třídě, studovat v zahraničí jako možnost rozvoje akcí.

Jedním z prvků algebry primitivní úrovně je logaritmus. Název pochází z řeckého jazyka od slova „číslo“ nebo „stupeň“ a znamená míru, do jaké je nutné zvýšit číslo v základně, aby bylo možné najít konečné číslo.

Druhy logaritmů

log a b - logaritmus čísla b k zakládání a (a> 0, a ≠ 1, b> 0);
lg b - desítkový logaritmus (základ logaritmu 10, a = 10);
ln b - přirozený logaritmus (základ logaritmu e, a = e).

Jak řešit logaritmy?

Logaritmická základna a z b je exponent, který vyžaduje, aby základna a byla zvýšena na b. Výsledek se vyslovuje takto: „logaritmus b založit a“. Řešení logaritmických problémů spočívá v tom, že musíte určit daný stupeň čísly podle uvedených čísel. Existuje několik základních pravidel pro určování nebo řešení logaritmu a také pro transformaci samotné položky. Pomocí nich je provedeno řešení logaritmických rovnic, nalezeny derivace, vyřešeny integrály a provedena řada dalších operací. V zásadě je řešením samotného logaritmu jeho zjednodušená notace. Níže jsou uvedeny základní vzorce a vlastnosti:

Pro jakýkoli a; a> 0; a ≠ 1 a pro libovolné x; y> 0.

a log a b = b - základní logaritmická identita
log a 1 = 0
log a a = 1
log a (x y) = log a x + log a y
log a x / y = log a x - log a y
log a 1 / x = -log a x
log a x p = p log a x
log a k x = 1 / k log a x, pro k ≠ 0
log a x = log a c x c
log a x = log b x / log b a - vzorec pro přechod na nový základ
log a x = 1 / log x a

Jak řešit logaritmy - podrobné pokyny k řešení

Nejprve si zapište požadovanou rovnici.

Poznámka: pokud je základní logaritmus 10, pak je položka zkrácena, získá se desítkový logaritmus. Pokud stojí za to přirozené číslo e, pak zapíšeme a redukujeme na přirozený logaritmus. To znamená, že výsledkem všech logaritmů je síla, na kterou je základní číslo zvýšeno pro získání čísla b.

Řešením je přímo vypočítat tento stupeň. Před řešením výrazu pomocí logaritmu je třeba jej zjednodušit podle pravidla, tj. Pomocí vzorců. Hlavní identity najdete tak, že se trochu vrátíte v článku.

Při sčítání a odčítání logaritmů se dvěma různými čísly, ale se stejnými bázemi, nahraďte jeden logaritmus součinem nebo dělením bac. V tomto případě můžete použít přechodový vzorec na jinou základnu (viz výše).

Pokud používáte výrazy ke zjednodušení logaritmu, je třeba vzít v úvahu některá omezení. A to je: základ logaritmu a je pouze kladné číslo, ale nerovná se jednomu. Číslo b, jako a, musí být větší než nula.

Existují případy, kdy zjednodušením výrazu nemůžete logaritmus vypočítat numericky. Stává se, že takový výraz nedává smysl, protože mnoho stupňů je iracionálních čísel. Za této podmínky ponechejte sílu čísla ve formě logaritmické notace.

Logaritmus b (b> 0) založit a (a> 0, a ≠ 1) Je exponent, na který musíte zvýšit číslo a, abyste dostali b.

Logaritmus b k základně 10 lze zapsat jako lg (b) a logaritmus základu e (přirozený logaritmus) je ln (b).

Často se používá při řešení problémů s logaritmy:

Vlastnosti logaritmů

Existují čtyři hlavní vlastnosti logaritmů.

Nechť a> 0, a ≠ 1, x> 0 a y> 0.

Vlastnost 1. Logaritmus produktu

Logaritmus produktu se rovná součtu logaritmů:

log a (x ⋅ y) = log a x + log a y

Vlastnost 2. Logaritmus kvocientu

Logaritmus kvocientu se rovná rozdílu logaritmů:

log a (x / y) = log a x - log a y

Vlastnost 3. Logaritmus stupně

Logaritmus stupně se rovná součinu síly logaritmem:

Pokud je základ logaritmu v moci, funguje další vzorec:

Vlastnost 4. Logaritmus kořene

Tuto vlastnost lze získat z vlastnosti logaritmu stupně, protože kořen n-tého stupně se rovná stupni 1 / n:

Vzorec pro přechod z logaritmu v jedné základně na logaritmus v jiné základně

Tento vzorec se také často používá při řešení různých problémů logaritmů:

Zvláštní případ:

Porovnání logaritmů (nerovností)

Předpokládejme, že máme 2 funkce f (x) a g (x) pod logaritmy se stejnými bázemi a mezi nimi je znak nerovnosti:

Chcete-li je porovnat, musíte se nejprve podívat na základ logaritmů a:

Pokud a> 0, pak f (x)> g (x)> 0
Pokud 0< a < 1, то 0 < f(x) < g(x)

Jak řešit problémy s logaritmy: příklady

Logaritmické úkoly zahrnuty v USE v matematice pro ročník 11 v úkolu 5 a úkolu 7, najdete úkoly s řešeními na našem webu v příslušných částech. Úkoly s logaritmy se také nacházejí v řadě úkolů z matematiky. Všechny příklady lze najít pomocí vyhledávání na webu.

Co je to logaritmus

Logaritmy byly vždy považovány za záludné téma školní kurz matematika. Existuje mnoho různých definic logaritmu, ale většina učebnic nějak používá ty nejobtížnější a nešťastné.

Logaritmus definujeme jednoduše a jasně. Za tímto účelem vytvořme tabulku:

Takže máme před sebou moc dvou.

Logaritmy - vlastnosti, vzorce, řešení

Pokud vezmete číslo ze spodního řádku, můžete snadno zjistit, do jaké míry musíte zvýšit dva, abyste získali toto číslo. Chcete-li například získat 16, musíte zvýšit dvě na čtvrtou sílu. A abyste získali 64, musíte zvýšit dvě na šestou sílu. To je vidět z tabulky.

A teď - vlastně definice logaritmu:

base a from argument x je síla, na kterou musí být číslo a zvýšeno, aby bylo získáno číslo x.

Notace: log a x = b, kde a je základ, x je argument, b je vlastně to, čím je logaritmus.

Například 2 3 = 8 ⇒log 2 8 = 3 (logická základna 2 z 8 jsou tři, protože 2 3 = 8). Se stejným logem úspěchu 2 64 = 6, protože 2 6 = 64.

Volá se operace hledání logaritmu čísla v dané základně. Přidejte tedy do naší tabulky nový řádek:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Ne všechny logaritmy se bohužel počítají tak snadno. Zkuste například najít log 2 5. Číslo 5 není v tabulce, ale logika určuje, že logaritmus bude ležet někde na segmentu. Protože 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Taková čísla se nazývají iracionální: čísla za desetinnou čárkou lze psát na neurčito a nikdy se neopakují. Pokud se logaritmus ukáže jako iracionální, je lepší to nechat tak: log 2 5, log 3 8, log 5 100.

Je důležité si uvědomit, že logaritmus je výraz se dvěma proměnnými (základ a argument). Zpočátku je mnoho lidí zmateno, kde je základ a kde je argument. Abyste se vyhnuli nepříjemným nedorozuměním, podívejte se na obrázek:

Před námi není nic jiného než definice logaritmu. Pamatovat si: logaritmus je stupeň ke kterému musí být zvýšena základna, aby se získal argument. Je to základna, která je zvýšena na sílu - na obrázku je zvýrazněna červeně. Ukazuje se, že základna je vždy dole! Toto nádherné pravidlo říkám svým studentům hned na první lekci - a nedochází ke zmatkům.

Jak počítat logaritmy

Přišli jsme na definici - zbývá se naučit počítat logaritmy, tj. zbavit se log logu. Nejprve si povšimneme, že z definice vyplývají dvě důležitá fakta:

Argument a radix musí být vždy větší než nula. Vyplývá to z definice stupně pomocí racionálního ukazatele, na který se definice logaritmu redukuje.
Základna se musí lišit od jedné, protože jedna je stále jedna do jakéhokoli stupně. Z tohoto důvodu je otázka „do jaké míry musí člověk vychovat jednoho, aby získal dvojku“, zbytečná. Takový titul neexistuje!

Taková omezení se nazývají rozsah platných hodnot(ODZ). Ukazuje se, že ODZ logaritmu vypadá takto: log a x = b ⇒x> 0, a> 0, a ≠ 1.

Upozorňujeme, že počet b (hodnota logaritmu) není nijak omezen. Například logaritmus může být záporný: log 2 0,5 = −1, protože 0,5 = 2 −1.

Nyní však uvažujeme pouze o numerických výrazech, kde znalost ODV logaritmu není nutná. Překladatelé úloh již zohlednili všechna omezení. Když ale přijdou logaritmické rovnice a nerovnosti, stanou se požadavky DHS povinné. Ve skutečnosti a v argumentu mohou existovat velmi silné konstrukce, které nemusí nutně odpovídat výše uvedeným omezením.

Nyní zvažte obecné schéma výpočet logaritmů. Skládá se ze tří kroků:

Prezentujte radix a a argument x jako mocninu s nejmenším možným radixem větším než jeden. Po cestě je lepší zbavit se desetinných míst;
Vyřešte rovnici pro proměnnou b: x = a b;
Výsledné číslo b bude odpovědí.

To je vše! Pokud se logaritmus ukáže jako iracionální, bude to vidět již v prvním kroku. Požadavek, aby základna byla větší než jedna, je velmi relevantní: snižuje se tím pravděpodobnost chyby a výrazně se zjednodušují výpočty. Podobně s desetinné zlomky: pokud je okamžitě přeložíte do běžných, bude chyb několikrát méně.

Podívejme se, jak toto schéma funguje, s konkrétními příklady:

Úkol. Vypočítejte logaritmus: log 5 25

Představme základnu a argument jako mocninu pěti: 5 = 5 1; 25 = 5 2;

Pojďme skládat a řešit rovnici:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒5 b = 5 2 ⇒ b = 2;

Obdržel odpověď: 2.

Úkol. Vypočítejte logaritmus:

Úkol. Vypočítejte protokol: log 4 64

Představme základ a argument jako mocninu dvou: 4 = 2 2; 64 = 2 6;
Pojďme skládat a řešit rovnici:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒2 2b = 2 6 ⇒2b = 6 ⇒ b = 3;
Obdržel odpověď: 3.

Úkol. Vypočítejte logaritmus: log 16 1

Představme základnu a argument jako mocninu dvou: 16 = 2 4; 1 = 2 0;
Pojďme skládat a řešit rovnici:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒2 4b = 2 0 ⇒4b = 0 ⇒ b = 0;
Dostal odpověď: 0.

Úkol. Vypočítejte protokol: protokolu 7 14

Představme základnu a argument jako mocninu sedmi: 7 = 7 1; 14 není reprezentován jako síla sedmi, protože 7 1< 14 < 7 2 ;
Z předchozího bodu vyplývá, že logaritmus se nepočítá;
Odpověď je beze změny: log 7 14.

Malá poznámka k poslednímu příkladu. Jak zajistíte, aby číslo nebylo přesnou silou jiného čísla? Je to velmi jednoduché - stačí to rozdělit na hlavní faktory. Pokud faktorizace obsahuje alespoň dva různé faktory, počet není přesnou silou.

Úkol. Zjistěte, zda jsou přesné síly čísla: 8; 48; 81; 35; čtrnáct.

8 = 2 2 2 = 2 3 - přesný stupeň, protože existuje pouze jeden faktor;
48 = 6,8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - není přesný stupeň, protože existují dva faktory: 3 a 2;
81 = 9 9 = 3 3 3 3 = 3 4 - přesný stupeň;
35 = 7,5 - opět není přesný stupeň;
14 = 7 2 - opět není přesný stupeň;

Všimněte si také, že samotná prvočísla jsou vždy jejich vlastní pravomocí.

Desetinný logaritmus

Některé logaritmy jsou tak běžné, že mají zvláštní název a označení.

argumentu x je základní 10 logaritmus, tj. síla, na kterou musí být zvýšeno číslo 10, aby bylo získáno číslo x. Označení: lg x.

Například lg 10 = 1; lg 100 = 2; lg 1000 = 3 - atd.

Od nynějška, když se v učebnici objeví fráze jako „Najít lg 0,01“, měli byste vědět: nejde o překlep. Toto je desítkový logaritmus. Pokud však na takové označení nejste zvyklí, můžete jej kdykoli přepsat:
log x = log 10 x

Všechno, co platí pro běžné logaritmy, platí také pro desetinná místa.

Přirozený logaritmus

Existuje další logaritmus, který má vlastní notaci. Svým způsobem je to ještě důležitější než desetinné číslo. to je o přirozeném logaritmu.

argumentu x je základ logaritmu e, tj. síla, na kterou musí být zvýšeno číslo e, aby bylo získáno číslo x. Označení: ln x.

Mnozí se ptají: co jiného je to číslo e? Toto je iracionální číslo, jeho přesný význam nelze najít a zapsat. Uvedu pouze jeho první čísla:
e = 2,718281828459 ...

Nebudeme se zabývat tím, co toto číslo je a proč je potřeba. Nezapomeňte, že e je základem přirozeného logaritmu:
ln x = log e x

Tedy ln e = 1; ln e2 = 2; ln e 16 = 16 - atd. Na druhou stranu ln 2 je iracionální číslo. Přirozený logaritmus jakéhokoli racionálního čísla je obecně iracionální. Kromě jednotek samozřejmě: ln 1 = 0.

Pro přirozené logaritmy platí všechna pravidla, která platí pro běžné logaritmy.

Viz také:

Logaritmus. Vlastnosti logaritmu (síla logaritmu).

Jak mohu představovat číslo jako logaritmus?

Používáme definici logaritmu.

Logaritmus je indikátorem míry, do jaké musí být základna zvýšena, aby se číslo dostalo pod znaménko logaritmu.

Abychom tedy mohli představovat nějaké číslo c ve formě logaritmu k základně a, je nutné dát mocninu se stejnou základnou jako základna logaritmu pod znak logaritmu a toto číslo c zapsat do exponent:

Ve formě logaritmu lze reprezentovat absolutně libovolné číslo - kladné, záporné, celé, zlomkové, racionální, iracionální:

Aby nedošlo k záměně aac za stresujících podmínek kontroly nebo zkoušky, můžete si zapamatovat následující pravidlo:

co je dole, jde dolů, co je nahoře, jde nahoru.

Například můžete chtít reprezentovat číslo 2 jako logaritmus k základu 3.

Máme dvě čísla - 2 a 3. Tato čísla jsou základ a exponent, které zapíšeme pod znaménkem logaritmu. Zbývá určit, které z těchto čísel je třeba zapsat na základ stupně a které - na exponent.

Základna 3 v logaritmu je dole, což znamená, že když reprezentujeme dva jako logaritmus k základně 3, 3 se také zapíše do základny.

2 stojí nad třemi. A když napíšeme mocninu dvou, napíšeme ji nad tři, tedy do exponentu:

Logaritmy. První úroveň.

Logaritmy

Logaritmus kladné číslo b z důvodu A kde a> 0, a ≠ 1, se nazývá exponent, na kterého musí být číslo zvýšeno A, Získat b.

Definice logaritmu lze stručně napsat takto:

Tato rovnost platí pro b> 0, a> 0, a ≠ 1. Obvykle se tomu říká logaritmická identita.
Akce nalezení logaritmu čísla se nazývá logaritmem.

Vlastnosti logaritmu:

Logaritmus produktu:

Logaritmus podílu dělení:

Výměna základny logaritmu:

Logaritmus stupně:

Logaritmus kořene:

Logaritmus výkonu:

Desetinné a přirozené logaritmy.

Desetinný logaritmusčísla volají základní 10 logaritmus tohoto čísla a píší & nbsp lg b
Přirozený logaritmusčísla volají základní logaritmus tohoto čísla E kde E- iracionální číslo, přibližně rovné 2,7. V tomto případě píší ln b.

Další poznámky k algebře a geometrii

Základní vlastnosti logaritmů

Logaritmy, stejně jako všechna čísla, lze sčítat, odečítat a transformovat jakýmkoli způsobem. Ale protože logaritmy nejsou úplně běžná čísla, existují zde pravidla, která se nazývají základní vlastnosti.

Tato pravidla je nutné znát - bez nich nelze vyřešit žádný vážný logaritmický problém. Navíc je jich velmi málo - vše se dá naučit za jeden den. Pojďme tedy začít.

Sčítání a odčítání logaritmů

Zvažte dva logaritmy se stejnými základnami: log a x a log a y. Pak je lze sčítat a odečítat a:

log a x + log a y = log a (x y);
log a x - log a y = log a (x: y).

Součet logaritmů se tedy rovná logaritmu produktu a rozdíl je logaritmus kvocientu. Klíčovým bodem zde je - stejné důvody... Pokud jsou důvody odlišné, tato pravidla nefungují!

Tyto vzorce vám pomohou vypočítat logaritmický výraz, i když se jeho jednotlivé části nepočítají (viz lekce „Co je to logaritmus“). Podívejte se na příklady - a podívejte se:

Log 6 4 + log 6 9.

Protože základy logaritmů jsou stejné, použijeme vzorec součtu:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Úkol. Najděte hodnotu výrazu: log 2 48 - log 2 3.

Báze jsou stejné, použijeme rozdílový vzorec:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Úkol. Najděte hodnotu výrazu: log 3 135 - log 3 5.

Základny jsou opět stejné, takže máme:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Jak vidíte, původní výrazy se skládají ze „špatných“ logaritmů, které se samostatně nepočítají. Ale po transformacích se získá zcela normální počet. Mnohé jsou postaveny na této skutečnosti. testovací papíry... Jakou kontrolu - takové výrazy se vší vážností (někdy - prakticky beze změny) nabízejí na zkoušce.

Odstranění exponenta z logaritmu

Nyní si úkol trochu zkomplikujme. Co když základ nebo argument logaritmu vychází z titulu? Potom lze exponenta tohoto stupně vyjmout ze znaménka logaritmu podle následujících pravidel:

Je snadné vidět, že poslední pravidlo následuje po prvních dvou. Je ale lepší si to pamatovat stejně - v některých případech to významně sníží množství výpočtu.

Všechna tato pravidla mají samozřejmě smysl, pokud je dodržena ODL logaritmu: a> 0, a ≠ 1, x> 0. A ještě jedna věc: naučit se používat všechny vzorce nejen zleva doprava, ale také naopak , tj můžete zadat čísla před znaménkem logaritmu do samotného logaritmu.

Jak řešit logaritmy

To je to, co je nejčastěji požadováno.

Úkol. Najděte hodnotu výrazu: log 7 49 6.

Zbavme se stupně v argumentu pomocí prvního vzorce:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Úkol. Najděte význam výrazu:

Všimněte si, že jmenovatel obsahuje logaritmus, jehož základem a argumentem jsou přesné mocniny: 16 = 2 4; 49 = 7 2. My máme:

Myslím, že poslední příklad potřebuje nějaké objasnění. Kde logaritmy zmizely? Dokud poslední moment pracujeme pouze se jmenovatelem. Představili jsme základ a argument tam stojícího logaritmu ve formě stupňů a vynesli ukazatele - dostali jsme „třípodlažní“ zlomek.

Nyní se podívejme na základní zlomek. Čitatel a jmenovatel obsahují stejné číslo: log 2 7. Od log 2 7 ≠ 0 můžeme zlomek zrušit - jmenovatel zůstane 2/4. Podle pravidel aritmetiky lze čtyři přenést do čitatele, což se stalo. Výsledkem byla odpověď: 2.

Přechod k novému základu

Když už mluvíme o pravidlech sčítání a odčítání logaritmů, konkrétně jsem zdůraznil, že fungují pouze na stejných základnách. Co když jsou důvody jiné? Co když to nejsou přesné síly stejného počtu?

Na pomoc se dostávají vzorce pro přechod na nový základ. Pojďme je formulovat jako větu:

Nechť logaritmus log a je uveden x. Pak platí pro libovolné číslo c takové, že c> 0 a c ≠ 1, následující rovnost:

Zejména pokud dáme c = x, dostaneme:

Z druhého vzorce vyplývá, že je možné zaměnit základ a argument logaritmu, ale v tomto případě je celý výraz „obrácen“, tj. logaritmus se objeví ve jmenovateli.

Tyto vzorce se zřídka vyskytují v běžných číselných výrazech. Je možné odhadnout, jak pohodlné jsou, pouze když řeší logaritmické rovnice a nerovnice.

Existují však úkoly, které se obecně nevyřeší, kromě přechodu na nový základ. Zvažte několik z nich:

Úkol. Najděte hodnotu výrazu: log 5 16 log 2 25.

Všimněte si, že argumenty obou logaritmů obsahují přesné stupně. Vyjměte ukazatele: log 5 16 = log 5 2 4 = 4 log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Nyní převrátíme druhý logaritmus:

Vzhledem k tomu, že se produkt nemění z permutace faktorů, jsme klidně vynásobili čtyři a dva a poté jsme se zabývali logaritmy.

Úkol. Najděte hodnotu výrazu: log 9 100 · lg 3.

Základ a argument prvního logaritmu jsou přesné stupně. Pojďme si to zapsat a zbavit se metrik:

Pojďme se zbavit desítkového logaritmu přesunem na novou základnu:

Základní logaritmická identita

V procesu řešení je často nutné představovat číslo jako logaritmus k dané základně.

V tomto případě nám vzorce pomohou:

V prvním případě se číslo n stává exponentem v argumentu. Číslo n může být naprosto cokoli, protože jde pouze o hodnotu logaritmu.

Druhý vzorec je ve skutečnosti parafrázovanou definicí. Říká se tomu :.

Co se vlastně stane, když je číslo b zvýšeno na takovou mocninu, že číslo b této mocnině dá číslu a? Máte pravdu: dostanete právě toto číslo a. Přečtěte si pozorně tento odstavec znovu - mnoho lidí na něm „visí“.

Stejně jako vzorce pro přechod na novou základnu je základní logaritmická identita někdy jediným možným řešením.

Úkol. Najděte význam výrazu:

Všimněte si, že log 25 64 = log 5 8 - právě přesunul čtverec ze základny a argument logaritmu. Vezmeme-li v úvahu pravidla pro násobení stupňů se stejnou základnou, dostaneme:

Pokud to někdo neví, byl to skutečný problém ze zkoušky 🙂

Logaritmická jednotka a logaritmická nula

Na závěr uvedu dvě identity, které lze jen stěží nazvat vlastnostmi - jsou to spíše důsledky definice logaritmu. Neustále se setkávají s problémy a překvapivě vytvářejí problémy i pro „pokročilé“ studenty.

log a a = 1 je. Pamatujte jednou provždy: logaritmus k jakékoli základně a z této základny se rovná jedné.
log a 1 = 0 je. Základem a může být cokoli, ale pokud je argument jeden, logaritmus je nulový! Protože 0 = 1 je přímým důsledkem definice.

To jsou všechny vlastnosti. Určitě si je procvičte v praxi! Stáhněte si cheat sheet na začátku lekce, vytiskněte jej a vyřešte problémy.

Takže máme před sebou moc dvou. Pokud vezmete číslo ze spodního řádku, můžete snadno zjistit, do jaké míry musíte zvýšit dva, abyste získali toto číslo. Chcete-li například získat 16, musíte zvýšit dvě na čtvrtou sílu. A abyste získali 64, musíte zvýšit dvě na šestou sílu. To je vidět z tabulky.

A teď - vlastně definice logaritmu:

Logaritmická základna a argumentu x je síla, na kterou musí být číslo a zvýšeno, aby bylo získáno číslo x.

Notace: log a x = b, kde a je základ, x je argument, b je vlastně to, čím je logaritmus.

Například 2 3 = 8 ⇒ log 2 8 = 3 (logická základna 2 z 8 jsou tři, protože 2 3 = 8). Se stejným logem úspěchu 2 64 = 6, protože 2 6 = 64.

Operace nalezení logaritmu čísla v dané základně se nazývá logaritmus. Přidejte tedy do naší tabulky nový řádek:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

Ne všechny logaritmy se bohužel počítají tak snadno. Zkuste například najít protokol 2 5. Číslo 5 není v tabulce, ale logika určuje, že logaritmus bude ležet někde v segmentu. Protože 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Přišli jsme na definici - zbývá se naučit počítat logaritmy, tj. zbavit se log logu. Nejprve si povšimneme, že z definice vyplývají dvě důležitá fakta:

Argument a radix musí být vždy větší než nula. Vyplývá to z definice stupně pomocí racionálního ukazatele, na který se definice logaritmu redukuje.
Základna se musí lišit od jedné, protože jedna je stále jedna do jakéhokoli stupně. Z tohoto důvodu je otázka „do jaké míry musí člověk vychovat jednoho, aby získal dvojku“, zbytečná. Takový titul neexistuje!

Taková omezení se nazývají rozsah platných hodnot(ODZ). Ukazuje se, že ODZ logaritmu vypadá takto: log a x = b ⇒ x> 0, a> 0, a ≠ 1.

Upozorňujeme, že počet b (hodnota logaritmu) není nijak omezen. Například logaritmus může být záporný: log 2 0,5 = −1, protože 0,5 = 2 −1.

Nyní se podívejme na obecné schéma pro výpočet logaritmů. Skládá se ze tří kroků:

Prezentujte radix a a argument x jako mocninu s nejmenším možným radixem větším než jeden. Po cestě je lepší zbavit se desetinných míst;
Vyřešte rovnici pro proměnnou b: x = a b;
Výsledné číslo b bude odpovědí.

To je vše! Pokud se logaritmus ukáže jako iracionální, bude to vidět již v prvním kroku. Požadavek, aby základna byla větší než jedna, je velmi relevantní: snižuje se tím pravděpodobnost chyby a výrazně se zjednodušují výpočty. Podobně s desetinnými zlomky: pokud je okamžitě převedete na běžné, bude chyb mnohokrát méně.

Podívejme se, jak toto schéma funguje, s konkrétními příklady:

Úkol. Vypočítejte logaritmus: log 5 25

Představme základnu a argument jako mocninu pěti: 5 = 5 1; 25 = 5 2;

Pojďme skládat a řešit rovnici:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;

Obdržel odpověď: 2.

Úkol. Vypočítejte logaritmus:

Úkol. Vypočítejte protokol: log 4 64

Představme základ a argument jako mocninu dvou: 4 = 2 2; 64 = 2 6;
Pojďme skládat a řešit rovnici:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
Obdržel odpověď: 3.

Úkol. Vypočítejte logaritmus: log 16 1

Představme základnu a argument jako mocninu dvou: 16 = 2 4; 1 = 2 0;
Pojďme skládat a řešit rovnici:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
Dostal odpověď: 0.

Úkol. Vypočítejte protokol: protokolu 7 14

Představme základnu a argument jako mocninu sedmi: 7 = 7 1; 14 není reprezentován jako síla sedmi, protože 7 1< 14 < 7 2 ;
Z předchozího bodu vyplývá, že logaritmus se nepočítá;
Odpověď je beze změny: log 7 14.

Úkol. Zjistěte, zda jsou přesné síly čísla: 8; 48; 81; 35; čtrnáct.

Všimněte si také, že samotná prvočísla jsou vždy jejich vlastní pravomocí.

Desetinný logaritmus

Některé logaritmy jsou tak běžné, že mají zvláštní název a označení.

Desetinný logaritmus x je základní 10 logaritmus, tj. síla, na kterou musí být zvýšeno číslo 10, aby bylo získáno číslo x. Označení: lg x.

Například lg 10 = 1; lg 100 = 2; lg 1000 = 3 - atd.

Všechno, co platí pro běžné logaritmy, platí také pro desetinná místa.

Přirozený logaritmus

Existuje další logaritmus, který má vlastní notaci. Svým způsobem je to ještě důležitější než desetinné číslo. Toto je přirozený logaritmus.

Přirozený logaritmus x je základ logaritmu e, tj. síla, na kterou musí být zvýšeno číslo e, aby bylo získáno číslo x. Označení: ln x.

Mnozí se ptají: co jiného je to číslo e? Toto je iracionální číslo, jeho přesný význam nelze najít a zapsat. Uvedu pouze jeho první čísla:
e = 2,718281828459 ...

Nebudeme se zabývat tím, co toto číslo je a proč je potřeba. Nezapomeňte, že e je základem přirozeného logaritmu:
ln x = log e x

Pro přirozené logaritmy platí všechna pravidla, která platí pro běžné logaritmy.