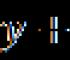Macierze i 2 x 3. Mnożenie macierzy: przykłady, algorytm działania, własności iloczynu

Matryca jest zdefiniowana jako prostokątny stół , geometrycznie jest prostokątem o wymiarach i ... Dwie macierze - dwa prostokąty: o wymiarach oraz , o wymiarach oraz ... Rozważając operację dodawania macierzy, ustalono wymaganie dopasowania rozmiarów prostokątów: =, =... To wymaganie zapewnia interakcję macierzy w systemach wektorowych:

=
-
- …-
- łańcuch sznurkowy,

=
-
- …-
- łańcuch kolumn,

ponadto, jeśli macierz przedstawiony na schemacie , to macierz powinny być przedstawione na tym samym schemacie. Ale najważniejsze: macierze oddziałują na grupy elementów - wektory!

Jeśli zdefiniujemy operację mnożenia macierzy w postaci: · =, pojawia się pytanie: ile wierszy i kolumn ma macierz ? To określiło tylko dwa możliwe schematy interakcji macierzy podczas ich mnożenia:

1* : wiersz lewej macierzy ↔ kolumna prawej macierzy,

2* : kolumna lewej macierzy ↔ wiersz prawej macierzy.

Dla schematu 1* : w matrycy ... Dla schematu 2* : w matrycy tyle wierszy ile macierz , jest tyle kolumn ile macierz .

W praktyce korzystanie ze schematu zostało naprawione 1* , który jest skrótem z reguły: kolumna wiersza .

Definicja:

Iloczyn macierzy oraz jest macierzą? ,których elementy są określone przez relację:
, dla wszystkich
,
, czyli obowiązuje zasadakolumna wiersza .

Komentarz: Z definicji iloczynu macierzy wynika: element jest równe produkt kropkowy smyczki- matryce za kolumnę matryce .

Własności działania mnożenia macierzy :

1* .
≠
- niemobilny (nie przemienny);

2* .
=
=
- kombinacyjne (skojarzeniowe).

3* .
=
+
- dystrybucja (dystrybucja).

Komentarz: należy pamiętać: w nieruchomości 1* w ogólnym przypadku może być tak, że macierz
istnieje i macierz
nie istnieje!

W związku z wprowadzeniem działania iloczynu macierzowego pojawia się pytanie: jak wykonać iloczyn macierzowy oraz uzyskać macierz transponowaną względem macierzy ... Jeśli transponowane macierze oznaczymy jako:
,
oraz
, prawdziwe jest następujące twierdzenie.

1) Przedstawmy iloczyn macierzy:
w postaci schematu kalkulacji elementów matryce :

2). Uwzględniając definicję transpozycji macierzy, przedstawiamy również równość
=
w formie podobnego schematu:

C ′

Widoczny: element matryce
równy elementowi macierze C.◄

Komentarz: Definicja transpozycji macierzy i udowodnione twierdzenie o transpozycji iloczynu macierzy będą wielokrotnie wykorzystywane przy rozważaniu wyznaczników i macierzy przekształceń liniowych w przestrzeniach wektorowych.

Przykład 4–05 : Oblicz iloczyn macierzy: C =A b =

.

Rozwiązanie:

A oraz b :

C b ;

Wykorzystanie szablonu technologicznego w postaci tabeli pozwoli na opracowanie algorytmu obliczania iloczynu macierzy i uchroni przed błędami obliczeń. Prześledźmy obliczenie kolumny 1 macierzy C: =
, =
.

Odpowiedź: C=
.

Przykład 4–06 : Oblicz iloczyn macierzy: C =A b =

.

Rozwiązanie:

W tabeli przedstawiono schemat obliczania iloczynu macierzy A oraz b :

▫ obliczyć kolumnę 1 macierzy C nad macierzą umieszczamy kolumnę-1 macierzy b ;

▫ aby obliczyć kolumnę-2 macierzy C nad macierzą umieszczamy kolumnę-2 macierzy b ;

C b ;

Kolumna

=, =, =.

Odpowiedź: =
.

Przykład 4–07 C=Ab=

.

Rozwiązanie:

W tabeli przedstawiono schemat obliczania iloczynu macierzy A oraz b :

▫ obliczyć kolumnę 1 macierzy C nad macierzą umieszczamy kolumnę-1 macierzy b ;

▫ aby obliczyć kolumnę-2 macierzy C nad macierzą umieszczamy kolumnę-2 macierzy b ;

▫ obliczyć kolumnę 3 macierzy C nad macierzą umieszczamy kolumnę 3 macierzy b ;

▫ obliczyć kolumnę 4 macierzy C nad macierzą umieszczamy kolumnę-4 macierzy b .

Kolumna	Kolumna	Kolumna	Kolumna

(Kontynuacja tabeli).

Kolumna	Kolumna	Kolumna	Kolumna

Z tabeli widzimy odpowiedź. Prześledźmy obliczenie kolumny 1 macierzy C:

=, =,

=, =.

Odpowiedź: C=
.

Przykład 4–08 : Oblicz: C=
, Jeśli A =
.

Rozwiązanie:

1) Napiszmy łańcuch wierszy-wektorów macierzy A:

(,0,0,...,0,...,0), (0,,0,...,0,...,0), ... , (0,0,0,...,),

i pomnóż (skalarnie) przez kolumnę- matryce A: (0,0, 0, ... , , ..., 0). Łatwo to zauważyć w matrycy C=
=
kolumna- przyjmie postać (0,0, 0, ..., , ..., 0). Oznacza to, że łańcuch łańcuch-wektor macierzy C =
przyjmie formę:

(,0,0,...,0,...,0), (0, , ...,0), ... , (0,0, 0, ... ,0, ..., ).

2) Jeśli teraz obliczymy C=
=
, to łańcuch wektorów wierszowych macierzy C =
przyjmie formę:

(,0,0,...,0,...,0), (0, ,0,...,0,...,0), ... , (0,0,0,..., , ...,0), ... , (0,0, 0, ... ,0, ..., ).

3) Zastosowanie metody indukcji matematycznej, dla macierzy C =
możemy pisać:

(,0,0,...,0,...,0), (0, ,0,...,0,...,0), ... , (0,0,0,..., , ...,0), ... , (0,0, 0, ... ,0, ..., ).

Odpowiedź: C=
.

Przykład 4–09 : Udowodnij, że jeśli macierze A oraz b- kwadratowy, ponadto
≠
, to zawsze prawdziwe są następujące stwierdzenia: a);

Rozwiązanie:

1) Biorąc pod uwagę rozdzielczą własność mnożenia macierzy:
=
+
, piszemy:

2) Biorąc pod uwagę rozdzielczą własność mnożenia macierzy:
=
+
, piszemy:

Odpowiedź: sprawdzone.

Przykład 4–10 : Znajdź wszystkie macierze dojeżdżające z macierzą: =.

Rozwiązanie:

1) Miejmy macierz: takie, że
=
... Biorąc pod uwagę zasadę mnożenia macierzy łatwo zauważyć, że mnożenie tych macierzy jest możliwe tylko wtedy, gdy macierz - kwadrat i taki sam wymiar jak macierz .

2) Weźmy: =
i napisz wyrażenie
=
:

C=Ab.

Kolumna

3 a + D

3 b + mi

3 C + F

3 D + g

3 mi + h

3 F + k

3 g

3 h

3 k

Z tabeli widzimy odpowiedź.

3) Teraz napiszmy wyrażenie
=
:

W tabeli przedstawiono schemat obliczania iloczynu macierzy D=bA.

Kolumna

3 a

a + 3 b

b + 3 C

3 D

d + 3e

e + 3f

3 g

g + 3h

h + 3k

Z tabeli widzimy odpowiedź.

4) Użyjmy równości:
→ otrzymujemy równania do obliczania macierzy :

3 a + D =3 a → D =0; 3 D + g =3 D → g =0; 3 b + mi =a + 3b → mi =a ; 3 mi + h =d + 3e → h =0;

3 h =g + 3h → h =h ; 3 C + F =b + 3c → F =b ; 3 F + k =e + 3f → k =mi ; 3 k =h + 3k → h =0.

5) Korzystając z otrzymanych równań możemy napisać: =
.

Odpowiedź: =
.

Przykład 4–11 : Udowodnij, że macierz: =
spełnia równanie: –(a+D) x+ogłoszenie–
=0.

Rozwiązanie:

Komentarz: omawiany przykład jest interesujący, ponieważ pokazuje udział w wyrażeniu macierzowym skalarny macierze:
=
.

1) Obliczmy:
=

=
;
=
.

2) Podstaw macierz do równania : , lub:

–
+
=
.

Odpowiedź: sprawdzone.

Przykład 4–12 : Oblicz iloczyn macierzy: A= (4 0 -2 3 1) i b=: a) AB; b) BA.

Komentarz: rozważany przykład jest interesujący, ponieważ jest niezwykle imponująco demonstruje nierówności :
.

Rozwiązanie:

a)
= (4 3 + 0 1 + (-2) (-1) + 3 5 + 1 2) = (31) to macierz jednoelementowa;

b)
=
=
.

Odpowiedź: macierze w tekście.

Definicja 1

Iloczyn macierzy (C = AB) jest operacją tylko dla dopasowanych macierzy A i B, w których liczba kolumn macierzy A jest równa liczbie wierszy macierzy B:

C m × n = A ⏟ m × p × B ⏟ p × n

Przykład 1

Podane macierze:

A = a (i j) rozmiary m × n;
B = b (i j) rozmiary p × n

Macierz C, której elementy c i j oblicza się według następującego wzoru:

c i j = a i 1 × b 1 j + a i 2 × b 2 j +. ... ... + a i p × b p j, i = 1,. ... ... m, j = 1,. ... ... m

Przykład 2

Obliczamy iloczyny AB = BA:

A = 1 2 1 0 1 2, B = 1 0 0 1 1 1

Rozwiązanie wykorzystujące regułę mnożenia macierzy:

A ⏟ 2 × 3 × B ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2

B ⏟ 3 × 2 × A ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3

Znaleziono iloczyn A B i B A, ale są to macierze o różnych rozmiarach: A B nie jest równe B A.

Właściwości mnożenia macierzy

Właściwości mnożenia macierzy:

(A B) C = A (B C) - asocjatywność mnożenia macierzy;
А (В + С) = А В + А С - rozdzielność mnożenia;
(A + B) C = A C + B C - rozdzielność mnożenia;
λ (А В) = (λ А) В

Przykład 1

Sprawdzanie właściwości nr 1: (A B) C = A (B C):

(A × B) × A = 1 2 3 4 × 5 6 7 8 × 1 0 0 2 = 19 22 43 50 × 1 0 0 2 = 19 44 43 100,

A (B × C) = 1 2 3 4 × 5 6 7 8 1 0 0 2 = 1 2 3 4 × 5 12 7 16 = 19 44 43 100.

Przykład 2

Sprawdzanie właściwości nr 2: A (B + C) = A B + A C:

A × (B + C) = 1 2 3 4 × 5 6 7 8 + 1 0 0 2 = 1 2 3 4 × 6 6 7 10 = 20 26 46 58,

A B + A C = 1 2 3 4 × 5 6 7 8 + 1 2 3 4 × 1 0 0 2 = 19 22 43 50 + 1 4 3 8 = 20 26 46 58.

Iloczyn trzech macierzy

Iloczyn trzech macierzy A B C oblicza się na 2 sposoby:

znajdź AB i pomnóż przez C: (AB) C;
lub znajdź najpierw B C, a następnie pomnóż A (BC).

Przykład 3

Mnożenie macierzy na 2 sposoby:

4 3 7 5 × - 28 93 38 - 126 × 7 3 2 1

Algorytm działań:

znajdź iloczyn 2 macierzy;
następnie ponownie znajdź iloczyn 2 macierzy.

1). A B = 4 3 7 5 × - 28 93 38 - 126 = 4 (-28) + 3 × 38 4 × 93 + 3 (- 126) 7 (-28) + 5 × 38 7 × 93 + 5 (- 126) = 2 - 6 - 6 21

2). А В С = (А В) С = 2–6–6 21 7 3 2 1 = 2 × 7–6 × 2 2 × 3–6 × 1–6 × 7 + 21 × 2–6 × 3 + 21 × 1 = 2 0 0 3.

Używamy wzoru A B C = (A B) C:

1). W С = - 28 93 38 - 126 7 3 2 1 = - 28 × 7 + 93 × 2 - 28 × 3 + 93 × 1 38 × 7 - 126 × 2 38 × 3 - 126 × 1 = - 10 9 14 - 12

2). A B C = (A B) C = 7 3 2 1 - 10 9 14 - 12 = 4 (- 10) + 3 × 14 4 × 9 + 3 (- 12) 7 (- 10) + 5 × 14 7 × 9 + 5 (- 12) = 2 0 0 3

Odpowiedź: 4 3 7 5 - 28 93 38 - 126 7 3 2 1 = 2 0 0 3

Mnożenie macierzy przez liczbę

Definicja 2

Iloczynem macierzy A przez liczbę k jest macierz B = A k tej samej wielkości, którą otrzymuje się z oryginału przez pomnożenie przez podaną liczbę wszystkich jej elementów:

b ja, j = k × a ja, j

Własności mnożenia macierzy przez liczbę:

1 × A = A
0 × A = macierz zerowa
k (A + B) = k A + k B
(k + n) A = k A + n A
(k × n) × A = k (n × A)

Przykład 4

Znajdź iloczyn macierzy A = 4 2 9 0 przez 5.

5 A = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0

Mnożenie macierzy-wektora

Definicja 3

Aby znaleźć iloczyn macierzy i wektora, należy pomnożyć zgodnie z zasadą „wiersz po kolumnie”:

jeśli pomnożysz macierz przez wektor kolumny, liczba kolumn w macierzy musi odpowiadać liczbie wierszy w wektorze kolumny;
wynik mnożenia wektora kolumnowego jest tylko wektorem kolumnowym:

А В = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а m 1 а m 2 ⋯ а mnb 1 b 2 ⋯ b 1 n = a 11 × b 1 + a 12 × b 2 + ⋯ + a 1 n × bna 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × bn ⋯ ⋯ ⋯ ⋯ am 1 × b 1 + am 2 × b 2 + ⋯ + amn × bn = c 1 c 2 c 1 m

jeśli pomnożysz macierz przez wektor wierszowy, to mnożona macierz musi być wyłącznie wektorem kolumnowym, a liczba kolumn musi odpowiadać liczbie kolumn w wektorze wierszowym:

А В = а а ⋯ а bb ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × bna 2 × b 1 a 2 × b 2 ⋯ a 2 × bn ⋯ ⋯ ⋯ ⋯ an × b 1 an × b 2 ⋯ an × bn = c 11 c 12 ⋯ c 1 nc 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ cn 1 cn 2 ⋯ cnn

Przykład 5

Znajdź iloczyn macierzy A i wektora kolumnowego B:

А В = 2 4 0 - 2 1 3 - 1 0 1 1 2 - 1 = 2 × 1 + 4 × 2 + 0 × (- 1) - 2 × 1 + 1 × 2 + 3 × (- 1) - 1 × 1 + 0 × 2 + 1 × (- 1) = 2 + 8 + 0 - 2 + 2 - 3 - 1 + 0 - 1 = 10 - 3 - 2

Przykład 6

Znajdź iloczyn macierzy A i wektora wierszowego B:

A = 3 2 0 - 1, B = - 1 1 0 2

А В = 3 2 0 1 × - 1 1 0 2 = 3 × (- 1) 3 × 1 3 × 0 3 × 2 2 × (- 1) 2 × 1 2 × 0 2 × 20 × (- 1) 0 × 1 0 × 0 0 × 2 1 × (- 1) 1 × 1 1 × 0 1 × 2 = - 3 3 0 6 - 2 2 0 4 0 0 0 0 - 1 1 0 2

Odpowiedź: A B = - 3 3 0 6 - 2 2 0 4 0 0 0 0 - 1 1 0 2

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl + Enter

Ten zestaw narzędzi pomoże Ci nauczyć się wykonywać operacje na macierzach: dodawanie (odejmowanie) macierzy, transpozycja macierzy, mnożenie macierzy, znajdowanie macierzy odwrotnej. Cały materiał jest przedstawiony w prostej i przystępnej formie, podane są odpowiednie przykłady, dzięki czemu nawet nieprzygotowana osoba może nauczyć się wykonywać czynności z macierzami. Do samodzielnego testowania i samotestowania możesz bezpłatnie pobrać kalkulator macierzy >>>.

Postaram się minimalizować obliczenia teoretyczne, w niektórych miejscach możliwe są wyjaśnienia „na palcach” i użycie nienaukowych terminów. Miłośników solidnej teorii proszę nie krytykować, naszym zadaniem jest nauczyć się wykonywać akcje z macierzami.

Dla SUPERSZYBKIEGO przygotowania na temat (kto jest „w ogniu”) jest intensywny kurs pdf Macierz, wyznacznik i test!

Matryca to prostokątny stół dowolnego elementy... Jak elementy rozważymy liczby, czyli macierze liczbowe. ELEMENT Jest terminem. Warto zapamiętać to określenie, będzie często spotykane, nie jest przypadkiem, że użyłam pogrubionej czcionki, aby go podkreślić.

Przeznaczenie: macierze są zwykle oznaczane wielkimi literami łacińskimi

Przykład: Rozważ macierz dwa na trzy:

Ta macierz składa się z sześciu elementy:

Wszystkie liczby (elementy) wewnątrz macierzy istnieją same, to znaczy nie ma mowy o jakimkolwiek odejmowaniu:

To tylko tabela (zestaw) liczb!

My też się zgodzimy nie przestawiaj numerów, chyba że w wyjaśnieniach zaznaczono inaczej. Każda liczba ma swoją własną lokalizację i nie można jej tasować!

Omawiana macierz ma dwa wiersze:

oraz trzy kolumny:

STANDARD: mówiąc o wielkości matrycy, to najpierw wskazać liczbę rzędów, a dopiero potem liczbę kolumn. Właśnie rozebraliśmy macierz dwa na trzy.

Jeśli liczba wierszy i kolumn w macierzy jest taka sama, wówczas nazywa się macierz kwadrat, na przykład: - macierz trzy na trzy.

Jeśli macierz ma jedną kolumnę lub jeden wiersz, to takie macierze są również nazywane wektory.

Tak naprawdę pojęcie macierzy znamy od czasów szkoły, rozważmy na przykład punkt o współrzędnych „x” i „gra”. Zasadniczo współrzędne punktu są zapisane w macierzy jeden na dwa. Nawiasem mówiąc, oto przykład dla Ciebie, dlaczego kolejność liczb ma znaczenie: i są to dwa zupełnie różne punkty płaszczyzny.

Przejdźmy teraz bezpośrednio do gabinetu akcje z macierzami:

1) Pierwsza akcja. Usunięcie minusa z matrycy (dodanie minusa do matrycy).

Powrót do naszej matrycy ... Jak mogłeś zauważyć, w tej macierzy jest zbyt wiele liczb ujemnych. Jest to bardzo niewygodne z punktu widzenia wykonywania różnych czynności za pomocą matrycy, niewygodne jest pisanie tylu minusów i po prostu brzydko wygląda to w projekcie.

Przenieś minus poza macierz, zmieniając znak KAŻDEGO elementu macierzy:

Na zero, jak rozumiesz, znak się nie zmienia, zero - w Afryce też jest zero.

Odwrotny przykład: ... Wygląda brzydko.

Dodajmy do macierzy minus, zmieniając znak KAŻDEGO elementu macierzy:

Cóż, wyszło znacznie ładniej. A co najważniejsze, ŁATWIEJ będzie wykonać dowolne czynności z matrycą. Bo jest taki matematyczny ludowy omen: im więcej wad, tym więcej zamieszania i błędów.

2) Druga akcja. Mnożenie macierzy przez liczbę.

Przykład:

To proste, aby pomnożyć macierz przez liczbę, potrzebujesz każdy element macierzy jest mnożony przez podaną liczbę. V w tym przypadku- trzy.

Kolejny przydatny przykład:

- mnożenie macierzy przez ułamek

Zobaczmy, co zrobić najpierw. NIE MA POTRZEBY:

Wpisywanie ułamka do macierzy NIE JEST KONIECZNE, po pierwsze komplikuje to tylko dalsze działania z macierzą, a po drugie utrudnia nauczycielowi sprawdzenie rozwiązania (zwłaszcza jeśli - ostateczna odpowiedź zadania).

A szczególnie, NIE MA POTRZEBY podziel każdy element macierzy przez minus siedem:

Z artykułu Matematyka dla manekinów, czyli od czego zacząć , pamiętamy, że ułamki dziesiętne z przecinkiem w wyższej matematyce staraj się unikać w każdy możliwy sposób.

Jedyna rzecz, która pożądany do zrobienia w tym przykładzie jest wprowadzenie minusa do macierzy:

Ale jeśli WSZYSTKO elementy macierzy były podzielne przez 7 bez reszty, wtedy byłoby możliwe (i konieczne!) dzielenie.

Przykład:

W takim przypadku możesz i NIEZBĘDNY pomnóż wszystkie elementy macierzy przez, ponieważ wszystkie liczby w macierzy są podzielne przez 2 bez reszty.

Uwaga: w teorii matematyki wyższej nie ma szkolnego pojęcia „podziału”. Zamiast wyrażenia „podziel to przez to” zawsze możesz powiedzieć „pomnóż to przez ułamek”. Oznacza to, że dzielenie jest szczególnym przypadkiem mnożenia.

3) Trzecia akcja. Transpozycja macierzy.

Aby transponować macierz, musisz wpisać jej wiersze do kolumn transponowanej macierzy.

Przykład:

Transpozycja macierzy

Tutaj jest tylko jedna linia i zgodnie z zasadą musi być wpisana do kolumny:

- transponowana macierz.

Transponowana macierz jest zwykle oznaczona indeksem górnym lub myślnikiem w prawym górnym rogu.

Przykład krok po kroku:

Transpozycja macierzy

Najpierw przepisujemy pierwszy wiersz do pierwszej kolumny:

Następnie przepisujemy drugą linię do drugiej kolumny:

Na koniec przepisujemy trzecią linię do trzeciej kolumny:

Gotowy. Z grubsza mówiąc, transpozycja oznacza odwrócenie matrycy na bok.

4) Działanie czwarte. Suma (różnica) macierzy.

Suma macierzy to prosta operacja.
NIE WSZYSTKIE MATRYCE MOGĄ SIĘ SKŁADAĆ. Aby wykonać dodawanie (odejmowanie) macierzy konieczne jest, aby były one tego samego ROZMIARU.

Na przykład, jeśli podana jest macierz dwa na dwa, to można ją dodać tylko z macierzą dwa na dwa i bez żadnej innej!

Przykład:

Dodaj macierze oraz

Aby dodać macierze, konieczne jest dodanie odpowiadających im elementów:

Dla różnicy macierzy zasada jest podobna, konieczne jest znalezienie różnicy odpowiednich elementów.

Przykład:

Znajdź różnicę macierzy ,

Jak decydować podany przykładłatwiej, żeby się nie pomylić? Wskazane jest, aby pozbyć się zbędnych minusów, w tym celu dodajemy minus do macierzy:

Uwaga: w teorii matematyki wyższej nie ma szkolnego pojęcia „odejmowania”. Zamiast mówić „odejmij to od tego”, zawsze możesz powiedzieć „dodaj do tego liczbę ujemną”. Oznacza to, że odejmowanie jest szczególnym przypadkiem dodawania.

5) Działanie piąte. Mnożenie macierzy.

Jakie macierze można mnożyć?

Aby macierz została pomnożona przez macierz, potrzebujesz aby ilość kolumn w macierzy była równa ilości rzędów macierzy.

Przykład:
Czy można pomnożyć macierz przez macierz?

Oznacza to, że możesz pomnożyć te macierze.

Ale jeśli macierze są przestawiane, to w tym przypadku mnożenie jest już niemożliwe!

Dlatego mnożenie nie jest możliwe:

Nierzadko zdarzają się zadania ze sztuczką, gdy uczeń proszony jest o pomnożenie macierzy, których mnożenie jest oczywiście niemożliwe.

Należy zauważyć, że w wielu przypadkach możliwe jest pomnożenie macierzy w obie strony.
Na przykład dla macierzy i możliwe jest zarówno mnożenie, jak i mnożenie

Macierze to tablice liczb, które są ze sobą połączone. Można na nich wykonać szereg różnych operacji, o których powiemy poniżej.

Wielkość matrycy zależy od jej Zamówienia- liczba linii $ m $ i kolumn $ n $, które są w nim obecne. Linie składają się z elementów na liniach poziomych, a kolumny z elementów na prostych liniach pionowych. Jeżeli liczba wierszy jest równa liczbie kolumn, kolejność danej tabeli jest określona tylko przez jedną wartość $ m = n $.

Uwaga 1

Dla dowolnego elementu macierzy numer wiersza, w którym się znajduje, jest zapisywany jako pierwszy w indeksie, a numer kolumny jako drugi, czyli wpis $ a_ (ij) $ oznacza, że element znajduje się w $ i $ -tym wierszu aw $ j $ - th kolumnie.

Dodawanie i odejmowanie

A więc o dodawaniu i odejmowaniu. Czynności te można wykonać tylko z macierzami ten sam rozmiar.

W celu wykonania tych czynności konieczne jest dodanie lub odjęcie każdego elementu macierzy z elementem innej macierzy w tej samej pozycji co element w pierwszej.

Jako przykład znajdźmy sumę $ A + B $, gdzie:

$ A = \ początek (pmatrix) a_ (11) & a_ (12) & a_ (13) \\ a_ (21) & a_ (22) & a_ (23) \\ a_ (31) & a_ (32) & a_ (33) \\ \ end (pmatrix) $

i $ B = \ początek (pmatrix) b_ (11) & b_ (12) & b_ (13) \\ b_ (21) & b_ (22) & b_ (23) \\ b_ (31) & b_ (32) & b_ (33) \\ \ koniec (pmatrix) $

Suma dowolnego elementu nowej wynikowej tablicy macierzy $ A + B $ jest równa $ a_ (ij) + b_ (ij) $, np. element o indeksie $ 11 $ to $ a_ (11) + b_ (11) $, a cały wynik wygląda tak:

$ A + B = \ początek (pmatrix) a_ (11) + b_ (11) & a_ (12) + b_ (12) & a_ (13) + b_ (13) \\ a_ (21) + b_ (21) & a_ (22) + b_ (22) & a_ (23) + b_ (23) \\ a_ (31) + b_ (31) & a_ (32) + b_ (32) & a_ (33) + b_ (33 ) \\ \ koniec (pmatrix) $

Odejmowanie dla dwóch macierzy $ A-B $ odbywa się w ten sam sposób, ale każdy element nowej macierzy wynikowej zostanie obliczony przy użyciu formuły $ a_ (ij) - b_ (ij) $.

Należy pamiętać, że dodawanie i odejmowanie macierzy jest możliwe tylko wtedy, gdy ich kolejność jest taka sama.

Przykład 1

Rozwiąż następujące przykłady macierzy: $ A + B $; $A-B$.

$ A = \ początek (pmatrix) 0 & 5 & 2 \\ 1 & -1 & 3 \\ -2 & 0 & 7 \\ \ koniec (pmatrix) $

$ B = \ początek (pmatrix) 0 & 3 & 2 \\ -4 & 0 & -1 \\ 0 & 7 & -3 \\ \ koniec (pmatrix) $

Wyjaśnienie:

Wykonujemy akcje dla każdej pary elementów $ a_ (ij) $ i $ b_ (ij) $, odpowiednio:

$ A + B = \ początek (pmacierz) 0 + 0 & 5 + 3 & 2 + 2 \\ 1-4 & -1 + 0 & 3 - 1 \\ -2 + 0 & 0 + 7 & 7 - 3 \ \ \ end (pmatrix) = \ begin (pmatrix) 0 & 8 & 4 \\ -3 & -1 & 2 \\ -2 & 7 & 4 \\ \ end (pmatrix) $

$ AB = \ początek (pmacierz) 0-0 & 5-3 & 2-2 \\ 1 + 4 & -1-0 & 3 + 1 \\ -2-0 & 0-7 & 7 + 3 \\ \ koniec (pmatrix) = \ początek (pmatrix) 0 & 2 & 0 \\ 5 & -1 & 4 \\ -2 & -7 & 10 \\ \ koniec (pmatrix) $

Mnożenie macierzy przez liczbę

Aby pomnożyć tablicę macierzy przez dowolną liczbę, należy pomnożyć przez tę liczbę każdy z jej elementów, czyli dowolny element nowej macierzy $ C $, co jest wynikiem iloczynu $ A $ przez $ λ $ będzie równe $ с_ (ij) = λ \ cdot a_ (ij) $.

Przykład 2

Pomnóż $ A $ przez $ λ $, gdzie $ A = \ begin (pmatrix) 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \ end (pmatrix) $ i $ λ = 5 USD

$ A \ cdot λ = 5 \ cdot \ begin (pmatrix) 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \ end (pmatrix) = \ begin (pmatrix) 1 \ cdot 5 i 0 \ cdot 5 i 2 \ cdot 5 \\ -1 \ cdot 5 i 3 \ cdot 5 i 0 \ cdot 5 \\ 2 \ cdot 5 i 1 \ cdot 5 i 3 \ cdot 5 \\ \ koniec (pmatrix ) = \ begin (pmatrix) 5 & 0 & 10 \\ -5 & 15 & 0 \\ 10 & 5 & 15 \\ \ end (pmatrix) $.

Tabele macierzy produktów

To zadanie jest nieco trudniejsze niż poprzednie, ale jednocześnie nie ma w nim też nic trudnego.

Aby pomnożyć dwie macierze $ A \ cdot B $, liczba kolumn w $ A $ musi odpowiadać liczbie wierszy w $ B $.

Matematycznie można to zapisać tak:

$ A_ (m \ razy n) \ cdot B_ (n \ razy p) = С_ (m \ razy p) $

Oznacza to, że widząc pomnożone oryginalne macierze, możesz od razu określić kolejność powstałej nowej. Na przykład, jeśli musisz pomnożyć $ A_ (3 \ razy 2) $ i $ B_ (2 \ razy 3) $ - wynik wyniesie 3 $ \ razy 3 $:

$ \ begin (pmatrix) a_ (11) & a_ (12) \\ a_ (21) & a_ (22) \\ a_ (31) & a_ (32) \\ \ end (pmatrix) \ times \ begin (pmatrix) ) b_ (11) & b_ (12) & b_ (13) \\ b_ (21) & b_ (22) & b_ (23) \\ b_ (31) & b_ (32) & b_ (33) \\ \ end ( pmatrix) = \ begin (pmatrix) & & \\ & & \\ & & \\ \ end (pmatrix) = \ begin (pmatrix) (a_ (11) b_ (11) + a_ (12) b_ (21 )) & (a_ (11) b_ (12) + a_ (12) b_ (22)) & (a_ (11) b_ (13) + a_ (12) b_ (23)) \\ (a_ (21) b_ (11) + a_ (22) b_ (21)) & (a_ (21) b_ (12) + a_ (22) b_ (22)) & (a_ (11) b_ (13) + a_ (22) b_ ( 23) ) \\ (a_ (31) b_ (11) + a_ (32) b_ (21)) & (a_ (31) b_ (12) + a_ (32) b_ (22)) & (a_ (31) b_ ( 13) + a_ (32) b_ (23) \\ \ end (pmatrix) $

Jeżeli liczba kolumn pierwszego czynnika macierzy nie pokrywa się z liczbą wierszy drugiego czynnika macierzy, nie można wykonać mnożenia.

Przykład 3

Rozwiąż przykład:

$ A \ razy B =? $ Jeśli $ A = \ begin (pmatrix) 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \ end (pmatrix) $ i $ B = \ początek (pmatrix) 3 & - 1 & 2 \\ -4 & 0 & 2 \\ 1 & 1 & 2 \\ \ koniec (pmatrix) $.

$ A \ razy B = \ begin (pmatrix) (1 \ cdot 3 + 0 \ cdot (-4) + 2 \ cdot 1) & (1 \ cdot (-1) + 0 \ cdot 0 + 2 \ cdot 1) & (1 \ cdot 2 + 0 \ cdot 2 + 2 \ cdot 2) \\ (-1) \ cdot 3 + 3 \ cdot (-4) + 0 \ cdot 1) & (-1 \ cdot (-1) + 3 \ cdot 0 + 0 \ cdot 1) & (-1 \ cdot 2 + 3 \ cdot 2 + 0 \ cdot 2) \\ (2 \ cdot 3 + 1 \ cdot (-4) + 3 \ cdot 1) & 2 \ cdot (-1) + 1 \ cdot 0 + 3 \ cdot 1) & (2 \ cdot 2 + 1 \ cdot 2 + 3 \ cdot 2) \\ \ end (pmatrix) $

$ A \ razy B = \ początek (pmatrix) (3 + 0+ 2) & (-1 + 0 + 2) & (2 + 0 + 4) \\ (-3-12 + 0) & (1 + 0 + 0) & (-2 + 6 + 0) \\ (6-4 + 3) & (-2 + 0 + 3) & (4 + 2 + 6) \\ \ koniec (pmacierz) = \ początek (pmacierz ) 5 i 1 i 6 \\ -15 i 1 i 4 \\ 5 i 1 i 12 \\ \ koniec (pmatrix) $.

Znajdowanie wyznacznika macierzy

Wyznacznik macierzy oznaczamy jako $ Δ $ lub $ \ det $.

Uwaga 2

Wyznacznik można znaleźć tylko dla odmian kwadratowych macierzy.

W najprostszym przypadku, gdy macierz składa się tylko z jednego elementu, jej wyznacznikiem jest ten element: $ det A = | a_ (11) | = a_ (11) $

Możesz obliczyć wyznacznik macierzy rzędu drugiego zgodnie z następującą zasadą:

Definicja 1

Wyznacznik macierzy o rozmiarze 2 jest równy różnicy iloczynów elementów na głównej przekątnej i iloczynu elementów na drugorzędnej przekątnej:

$ \ begin (tablica) (| cc |) a_ (11) & a_ (12) \\ a_ (21) & a_ (22) \\ \ end (tablica) = a_ (11) \ cdot a_ (22) - a_ (12) \ cdot a_ (21) $

Jeśli wyznacznik macierzy jest ustawiony w rozmiarze 3 $ \ razy 3 $, to możesz go znaleźć za pomocą reguł mnemonicznych: Sarrus lub trójkąty, możesz również rozwinąć macierz o wiersz lub kolumnę, albo skorzystać z przekształceń Gaussa.

W przypadku większych wyznaczników można zastosować transformaty Gaussa i rozkład linii.

macierze odwrotne

Analogicznie do zwykłego mnożenia liczby przez jej odwrotność $ (1+ \ frac1x = 1) $, mnożenie odwrotności $ A ^ (- 1) $ przez pierwotną macierz daje w wyniku macierz jednostkową $ E $.

Najprostszą metodą rozwiązania przy szukaniu macierzy odwrotnej jest Jordan-Gauss... Jednostka tej samej wielkości jest zapisywana obok matrycy świnki morskiej, a następnie pierwotna jest redukowana do jednostki za pomocą przekształceń, a wszystkie wykonane czynności są powtarzane za pomocą $ E $.

Przykład 4

Biorąc pod uwagę $ A = \ begin (pmatrix) (cc) 1 & 2 \\ 3 & 4 \\ \ end (pmatrix) $

Uzyskaj odwrotność macierzy.

Rozwiązanie:

Piszemy razem $ A $ a na prawo od niego odpowiedni rozmiar $ E $:

$ \ begin (tablica) (cc | cc) 1 & 2 & 1 & 0 \\ 3 & 4 & 0 & 1 \\ \ end (tablica) $

Dostajemy zero w ostatniej linii na pierwszej pozycji: dodajemy do niej górną, pomnożoną przez $ -3 $:

$ \ begin (tablica) (cc | cc) 1 & 2 & 1 & 0 \\ 0 & -2 & -3 & 1 \\ \ end (tablica) $

Teraz wyzerujemy ostatni element pierwszej linii. Aby to zrobić, dodaj dół do górnej linii:

$ \ begin (tablica) (cc | cc) 1 & 0 & -2 & 1 \\ 0 & -2 & -3 & 1 \\ \ end (tablica) $

Podziel drugą przez $ -2 $:

$ \ begin (tablica) (cc | cc) 1 & 0 & -2 & 1 \\ 0 & 1 & 3/2 & -1/2 \\ \ end (tablica) $

Otrzymaliśmy wynik:

$ A = \ begin (pmatrix) (cc) -2 & 1 \\ 3/2 & -1/2 \\ \ end (pmatrix) $

Tabele macierzy transpozycji

Transpozycja to zmiana pozycji wierszy i kolumn w macierzy lub wyznaczniku przy zachowaniu ich pierwotnej kolejności. Wyznacznik tablicy transponowanej macierzy $ A ^ T $ będzie równy wyznacznikowi macierzy pierwotnej $ A $.

Przykład 5

Transponuj macierz $ A $ i sprawdź się, znajdując wyznacznik $ A $ i transponowaną płytkę macierzy.

$ A = \ początek (pmatrix) 1 & 2 & 3 \\ 4 & 5 & 6 \\ - 1 & -2 & -3 \\ \ koniec (pmatrix) $

Rozwiązanie:

Zastosujmy metodę Sarrusa dla wyznacznika:

$ \ det A = 1 \ cdot 5 \ cdot (-3) + 2 \ cdot 6 \ cdot (-1) + 3 \ cdot 4 \ cdot (-2) - 2 \ cdot 4 \ cdot (-3) - 1 \ cdot 6 \ cdot (-2) - 3 \ cdot 5 \ cdot (-1) = -15 - 12 - 24+ 24 + 12 + 15 = 0 $.

Mamy zdegenerowaną macierz.

Teraz przetransponujemy $ A $, w tym celu upuścimy macierz po jej prawej stronie:

$ A ^ T = \ początek (pmatrix) 1 & 4 & -1 \\ 2 & 5 & -2 \\ 3 & 6 & -3 \\ \ koniec (pmatrix) $

Znajdź wyznacznik dla $ A ^ T $ używając tej samej reguły:

$ det A ^ T = 1 \ cdot 5 \ cdot (-3) + 4 \ cdot (-2) \ cdot 3 + (-1) \ cdot 2 \ cdot 6 - 4 \ cdot 2 \ cdot (-3) - 1 \ cdot (-2) \ cdot 6 - (- 1) \ cdot 5 \ cdot 3 = - 15 -24 - 12 + 24 + 12 + 15 = 0 $.