Періодичні десяткові дроби. Звичайні та десяткові дроби і дії над ними

Уже в початковій школі учні стикаються з дробом. І потім вони з'являються в кожній темі. Забувати дії з цими числами можна. Тому потрібно знати всю інформацію про звичайні і десяткові дроби. Поняття ці нескладні, головне - розбиратися у всьому по порядку.

Навіщо потрібні дроби?

Навколишній світ складається з цілих предметів. Тому в частках необхідності немає. зате повсякденне життя постійно наштовхує людей на роботу з частинами предметів і речей.

Наприклад, шоколад складається з декількох часточок. Розглянемо ситуацію, коли його плитка утворена дванадцятьма прямокутниками. Якщо її розділити на двох, то вийде по 6 частин. Вона добре розділиться і на трьох. А ось п'ятьом не вдасться дати по цілому числу часточок шоколаду.

До речі, ці часточки - вже дробу. А подальше їх розподіл призводить до появи більш складних чисел.

Що таке «дріб»?

Це число, що складається з частин одиниці. Зовні воно виглядає як два числа, розділені горизонтальною або похилою рискою. Ця риса носить назву дробової. Число, записане зверху (зліва), називається чисельником. Те, що варто знизу (праворуч), є знаменником.

По суті, подрібнена риса виявляється знаком ділення. Тобто чисельник можна назвати діленим, а знаменник - дільником.

Які існують дроби?

В математиці їх є всього два види: звичайні і десяткові дроби. З першими школярі знайомляться в початкових класах, Називаючи їх просто «дроби». Другі дізнаються в 5 класі. Саме тоді з'являються ці назви.

Звичайні дроби - все ті, що записуються у вигляді двох чисел, розділених рисою. Наприклад, 4/7. Десяткова - це число, в якому дрібна частина має позиційну запис і відділяється від цілої за допомогою коми. Наприклад, 4,7. Учням потрібно чітко усвідомити, що два наведених прикладу - це абсолютно різні числа.

Кожну простий дріб можна записати у вигляді десяткового. Це твердження майже завжди вірно і в зворотному напрямку. Існують правила, які дозволяють записати звичайної дробом десяткову дріб.

Які підвиди мають зазначені види дробів?

Почати краще в хронологічному порядку, Так як вони вивчаються. першими йдуть звичайні дроби. Серед них можна виділити 5 підвидів.

Правильна. Її чисельник завжди менше знаменника.

Неправильна. У неї чисельник більше або дорівнює знаменника.

Скоротна / нескоротний. Вона може виявитися як правильною, так і неправильної. Важливо інше, чи є у чисельника зі знаменником загальні множники. Якщо є, то на них покладається розділити обидві частини дробу, тобто скоротити її.

Змішана. До її звичної правильної (неправильної) дробової частини приписується ціле число. Причому воно завжди стоїть зліва.

Складова. Вона утворюється з двох розділених один на одного дробів. Тобто в ній налічується відразу три дробові риси.

У десяткових дробів є всього два підвиди:

кінцева, тобто та, у якої дрібна частина обмежена (має кінець);

нескінченна - число, у якого цифри після коми не закінчуються (їх можна писати нескінченно).

Як переводити десяткову дріб в звичайну?

Якщо це кінцеве число, то застосовується асоціація, заснована на правилі - як чую, так пишу. Тобто потрібно правильно прочитати її і записати, але вже без коми, а з дробовою рискою.

В якості підказки про необхідному знаменнику, потрібно запам'ятати, що він завжди одиниця і кілька нулів. Останніх потрібно написати стільки, скільки цифр у дробовій частині розглянутого числа.

Як перевести десяткові дроби в звичайні, якщо їх ціла частина відсутня, тобто дорівнює нулю? Наприклад, 0,9 або 0,05. Після застосування зазначеного правила, виходить, що потрібно написати нуль цілих. Але воно не вказується. Залишається записати тільки дробові частини. У першого числа знаменник буде дорівнює 10, у другого - 100. Тобто зазначені приклади відповідями матимуть числа: 9/10, 5/100. Причому останнім виявляється можна скоротити на 5. Тому результатом для неї потрібно записати 1/20.

Як з десяткового дробу зробити звичайну, якщо її ціла частина відмінна від нуля? Наприклад, 5,23 або 13,00108. В обох прикладах читається ціла частина і записується її значення. У першому випадку це - 5, у другому - 13. Потім потрібно переходити до дробової частини. З ними покладається провести ту ж операцію. У першого числа з'являється 23/100, у другого - 108/100000. Друге значення знову потрібно скоротити. У відповіді виходять такі змішані дроби: 5 23/100 і 13 27/25000.

Як перевести нескінченну десяткову дріб в звичайну?

Якщо вона є неперіодичної, то таку операцію провести не вдасться. Цей факт пов'язаний з тим, що кожна десяткова дріб завжди перекладається або в кінцеву або в періодичну.

Єдине, що допускається робити з такою дробом, - це округляти її. Але тоді десяткова буде приблизно дорівнює тій нескінченною. Її вже можна перетворити в звичайну. Але зворотний процес: переклад в десяткову - ніколи не дасть початкового значення. Тобто нескінченні неперіодичні дроби в звичайні не перекладаються. Це потрібно запам'ятати.

Як записати нескінченну періодичну дріб у вигляді звичайного?

У цих числах після коми завжди з'являються одна або кілька цифр, які повторюються. Їх називають періодом. Наприклад, 0,3 (3). Тут «3» в періоді. Їх відносять до класу раціональних, так як можуть бути перетворені в звичайні дроби.

Тим, хто зустрічався з періодичними дробами, відомо, що вони можуть бути чистими або змішаними. У першому випадку період починається відразу від коми. У другому - дрібна частина починається з будь-яких цифр, а потім починається повтор.

Правило, за яким потрібно записати у вигляді звичайного дробу нескінченну десяткову, буде різним для зазначених двох видів чисел. Чисті періодичні дроби записати звичайними досить просто. Як з кінцевими, їх потрібно перетворити: в чисельник записати період, а знаменником буде цифра 9, що повторюється стільки раз, скільки цифр містить період.

Наприклад, 0, (5). Цілої частини у числа немає, тому відразу потрібно приступати до дробової. У чисельник записати 5, а в знаменник одну 9. Тобто відповіддю буде дріб 5/9.

Правило про те, як записати звичайної десяткову періодичну дріб, що є змішаною.

Подивитися на довжину періоду. Стільки 9 матиме знаменник.

Записати знаменник: спочатку дев'ятки, потім нулі.

Щоб визначити чисельник, потрібно записати різницю двох чисел. Зменшуваним будуть всі цифри після коми, разом з періодом. Від'ємником - воно ж без періоду.

Наприклад, 0,5 (8) - запишіть періодичну десяткову дріб у вигляді звичайного. У дробової частини до періоду варто одна цифра. Значить нуль буде один. У періоді теж тільки одна цифра - 8. Тобто дев'ятка одна. Тобто в знаменнику потрібно написати 90.

Для визначення чисельника з 58 потрібно відняти 5. Виходить 53. Відповіддю наприклад доведеться записати 53/90.

Як переводяться звичайні дроби в десяткові?

Найпростішим варіантом виявляється число, в знаменнику якого стоїть число 10, 100 та інше. Тоді знаменник просто відкидається, а між дробової і цілої частинами ставиться кома.

Бувають ситуації, коли знаменник легко перетворюється в 10, 100 і т. Д. Наприклад, числа 5, 20, 25. Їх досить помножити на 2, 5 і 4 відповідно. Тільки множити покладається не тільки знаменник, а й чисельник на те ж число.

Для всіх інших випадків стане в нагоді просте правило: розділити чисельник на знаменник. В цьому випадку може вийти два варіанти відповідей: кінцева або періодична десяткова дріб.

Дії зі звичайними дробами

Додавання і віднімання

З ними учні знайомляться раніше інших. Причому спочатку у дробів однакові знаменники, а потім різні. Загальні правила можна звести до такого плану.

Знайти найменше спільне кратне знаменників.

Записати додаткові множники до всіх звичайним дробям.

Помножити числители і знаменники на певні для них множники.

Скласти (відняти) числители дробів, а загальний знаменник залишити без зміни.

Якщо чисельник зменшуваного менше від'ємника, то потрібно з'ясувати, перед нами змішане число або правильна дріб.

У першому випадку у цілій частині потрібно зайняти одиницю. До чисельника дробу додати знаменник. А потім виконувати віднімання.

У другому - необхідно застосувати правило вирахування з меншого числа більшого. Тобто з модуля від'ємника відняти модуль зменшуваного, а у відповідь поставити знак «-».

Уважно подивитися на результат складання (вирахування). Якщо вийшла неправильна дріб, то належить виділити цілу частину. Тобто розділити чисельник на знаменник.

Множення і ділення

Для їх виконання дробу не потрібно приводити до спільного знаменника. Це спрощує виконання дій. Але в них все одно покладається слідувати правилам.

При множенні звичайних дробів необхідно розглянути числа в чисельнику і знаменниках. Якщо який-небудь чисельник і знаменник мають спільний множник, то їх можна скоротити.

Перемножити числители.

Перемножити знаменники.

Якщо вийшла скоротна дріб, то її потрібно було знову спростити.

При розподілі потрібно спочатку замінити поділ на множення, а дільник (другу дріб) - на зворотну дріб (поміняти місцями чисельник і знаменник).

Потім діяти, як при множенні (починаючи з пункту 1).

У завданнях, де помножити (ділити) потрібно на ціле число, останнє покладається записати у вигляді неправильного дробу. Тобто зі знаменником 1. Потім діяти, як було описано вище.

Дії з десятковими дробами

Додавання і віднімання

Звичайно, завжди можна перетворити десяткову дріб в звичайну. І діяти по вже описаному плану. Але іноді зручніше діяти без цього перекладу. Тоді правила для їх додавання і віднімання будуть абсолютно однаковими.

Зрівняти число цифр у дробовій частині числа, тобто після коми. Приписати в ній відсутня кількість нулів.

Записати дробу так, щоб кома була під коми.

Скласти (відняти) як натуральні числа.

Знести кому.

Множення і ділення

Важливо, що тут не потрібно дописувати нулі. Дробу покладається залишати в тому вигляді, як вони дані в прикладі. А далі йти за планом.

Для множення потрібно написати дробу одна під інший, не звертаючи увагу на коми.

Помножити, як натуральні числа.

Поставити у відповіді кому, відрахувавши від правого кінця відповіді стільки цифр, скільки їх стоїть в дрібних частинах обох множників.

Для поділу потрібно спочатку перетворити дільник: зробити його натуральним числом. Тобто помножити його на 10, 100 і т. Д., В залежності від того, скільки цифр у дробовій частині подільника.

На той же число помножити ділене.

Розділити десяткову дріб на натуральне число.

Поставити у відповіді кому в той момент, коли закінчиться розподіл цілої частини.

Як бути, якщо в одному прикладі є обидва види дробів?

Так в математиці часто зустрічаються приклади, в яких потрібно виконати дії над звичайними і десятковими дробами. У таких завданнях можливі два шляхи вирішення. Потрібно об'єктивно зважити числа і вибрати оптимальний.

Перший шлях: уявити звичайні десятковими

Він підходить, якщо при розподілі або перекладі виходять кінцеві дробу. Якщо хоча б одне число дає періодичну частину, то цей прийом застосовувати заборонено. Тому, навіть якщо не подобається працювати з звичайними дробами, доведеться рахувати їх.

Другий шлях: записати десяткові дроби звичайними

Цей прийом виявляється зручним, якщо в частині після коми стоять 1-2 цифри. Якщо їх більше, може вийти дуже велика звичайна дріб і десяткові записи дозволять порахувати завдання швидше і простіше. Тому завжди потрібно тверезо оцінювати завдання і вибирати найпростіший метод вирішення.

Ця стаття про десяткові дроби. Тут ми розберемося з десятковою маються на записом дробових чисел, введемо поняття десяткового дробу і наведемо приклади десяткових дробів. Далі поговоримо про розрядах десяткових дробів, дамо назви розрядів. Після цього зупинимося на нескінченних десяткових дробах, скажімо про періодичних і неперіодичних дробах. Далі перерахуємо основні дії з десятковими дробами. На закінчення встановимо положення десяткових дробів на координатному промені.

Навігація по сторінці.

Десяткова запис дробового числа

Читання десяткових дробів

Скажімо пару слів про правила читання десяткових дробів.

Десяткові дроби, яким відповідають правильні звичайні дроби, читаються також як і ці звичайні дроби, тільки ще попередньо додається «нуль цілих». Наприклад, десяткового дробу 0,12 відповідає звичайна дріб 12/100 (читається «дванадцять сотих»), тому, 0,12 читається як «нуль цілих дванадцять сотих».

Десяткові дроби, яким відповідають змішані числа, читаються абсолютно також як ці змішані числа. Наприклад, десяткового дробу 56,002 відповідає змішане число, тому, десяткова дріб 56,002 читається як «п'ятдесят шість цілих дві тисячних».

Розряди в десяткових дробах

У записі десяткових дробів, також як і в запису натуральних чисел, Значення кожної цифри залежить від її позиції. Дійсно, цифра 3 в десяткового дробу 0,3 означає три десятих, в десяткового дробу 0,0003 - три десяти тисячних, а в десяткового дробу 30 000,152 - три десятка тисяч. Таким чином, ми можемо говорити про розрядах в десяткових дробах, Так само як і про розрядах в натуральних числах.

Назви розрядів в десяткового дробу до десяткової коми повністю збігаються з назвами розрядів в натуральних числах. А назви розрядів в десяткового дробу після коми видно з наступної таблиці.

Наприклад, в десяткового дробу 37,051 цифра 3 знаходиться в розряді десятків, 7 - в розряді одиниць, 0 варто в розряді десятих, 5 - в розряді сотих, 1 - в розряді тисячних.

Розряди в десяткового дробу також розрізняються по старшинству. Якщо в запису десяткового дробу рухатися від цифри до цифри зліва на право, то ми будемо переміщатися від старших до молодшим розрядам. Наприклад, розряд сотень старше розряду десятих, а розряд мільйонних молодше розряду сотих. У даній кінцевій десяткового дробу можна говорити про старшого і молодшого розряді. Наприклад, в десяткового дробу 604,9387 старшим (вищим) розрядом є розряд сотень, а молодшим (нижчим) - розряд десятитисячних.

Для десяткових дробів має місце розкладання за розрядами. Воно аналогічно розкладанню за розрядами натуральних чисел. Наприклад, розкладання за розрядами десяткового дробу 45,6072 таке: 45,6072 \u003d 40 + 5 + 0,6 + 0,007 + 0,0002. А властивості складання від розкладання десяткового дробу за розрядами дозволяють перейти до інших уявленням цієї десяткового дробу, наприклад, 45,6072 \u003d 45 + 0,6072, або 45,6072 \u003d 40,6 + 5,007 + 0,0002, або 45,6072 \u003d 45,0072 + 0,6.

Кінцеві десяткові дроби

До цього моменту ми говорили лише про десяткових дробах, в записі яких після десяткової коми перебуває кінцеве число цифр. Такі дробу називають кінцевими десятковими дробами.

Визначення.

Кінцеві десяткові дроби - це десяткові дроби, в записах яких міститься кінцеве число знаків (цифр).

Наведемо кілька прикладів кінцевих десяткових дробів: 0,317, 3,5, +51,1020304958, 230 032,45.

Однак не всяка звичайна дріб може бути представлена \u200b\u200bу вигляді кінцевої десяткового дробу. Наприклад, дріб 5/13 не може бути замінена рівної їй дробом з одним з знаменників 10, 100, ..., отже, не може бути переведена в кінцеву десяткову дріб. Детальніше про це ми поговоримо в розділі теорії переклад звичайних дробів на десяткові дроби.

Нескінченні десяткові дроби: періодичні дроби і неперіодичні дроби

У записі десяткового дробу після коми можна допустити можливість наявності нескінченної кількості цифр. В цьому випадку ми прийдемо до розгляду так званих нескінченних десяткових дробів.

Визначення.

Нескінченні десяткові дроби - це десяткові дроби, в записі яких знаходиться безліч цифр.

Зрозуміло, що нескінченні десяткові дроби ми не можемо записати в повному вигляді, тому в їх запису обмежуються лише деяким кінцевим числом цифр після коми і ставлять три крапки, що вказує на нескінченно триваючу послідовність цифр. Наведемо кілька прикладів нескінченних десяткових дробів: 0,143940932 ..., +3,1415935432 ..., +153,02003004005 ..., 2,111111111 ..., +69,74152152152 ....

Якщо уважно подивитися на дві останні нескінченні десяткові дроби, то в дроби 2,111111111 ... добре видно нескінченно повторюється цифра 1, а в дроби +69,74152152152 ..., починаючи з третього знака після коми, чітко видно, що повторюється група цифр 1, 5 і 2. Такі нескінченні десяткові дроби називають періодичними.

Визначення.

Періодичні десяткові дроби (або просто періодичні дроби) - це нескінченні десяткові дроби, в записі яких, починаючи з деякого знака після коми, нескінченно повторюється якась цифра або група цифр, яку називають періодом дробу.

Наприклад, періодом періодичної дробу 2,111111111 ... є цифра 1, а періодом дробу +69,74152152152 ... є група цифр виду 152.

Для нескінченних періодичних десяткових дробів прийнята особлива форма запису. Для стислості домовилися період записувати один раз, укладаючи його в круглі дужки. Наприклад, періодична дріб 2,111111111 ... записується як 2, (1), а періодичний дріб +69,74152152152 ... записується як 69,74 (152).

Варто зазначити, що для однієї і тієї ж періодичного десяткового дробу можна вказати різні періоди. Наприклад, періодичну десяткову дріб 0,73333 ... можна розглядати як дріб 0,7 (3) з періодом 3, а також як дріб 0,7 (33) з періодом 33, і так далі 0,7 (333), 0,7 (3333), ... Також на періодичну дріб 0,73333 ... можна подивитися і так: 0,733 (3), або так 0,73 (333) і т.п. Тут, щоб уникнути багатозначності і різночитань, домовимося розглядати в якості періоду десяткового дробу найкоротшу з усіх можливих послідовностей повторюваних цифр, і починається з найближчою позиції до десяткової коми. Тобто, періодом десяткового дробу 0,73333 ... будемо вважати послідовність з однієї цифри 3, і періодичність починається з другої позиції після коми, тобто, 0,73333 ... \u003d 0,7 (3). Ще приклад: періодична дріб +4,7412121212 ... має період 12, періодичність починається з третьої цифри після коми, тобто, +4,7412121212 ... \u003d 4,74 (12).

Нескінченні десяткові періодичні дроби виходять при перекладі в десяткові дроби звичайних дробів, знаменники яких містять прості множники, відмінні від 2 і 5.

Тут же варто сказати про періодичні дроби з періодом 9. Наведемо приклади таких дробів: 6,43 (9), 27, (9). Ці дробу є іншим записом періодичних дробів з періодом 0, і їх прийнято замінювати періодичними дробами з періодом 0. Для цього період 9 замінюють періодом 0, а значення наступного за старшинством розряду збільшують на одиницю. Наприклад, дріб з періодом 9 виду 7,24 (9) замінюється періодичної дробом з періодом 0 виду 7,25 (0) або рівною їй кінцевої десятковим дробом 7,25. Ще приклад: 4, (9) \u003d 5, (0) \u003d 5. Рівність дроби з періодом 9 і відповідної їй дроби з періодом 0 легко встановлюється, після заміни цих десяткових дробів рівними їм звичайними дробами.

Нарешті, уважніше розглянемо нескінченні десяткові дроби, в записі яких відсутня нескінченно повторюється послідовність цифр. Їх називають непериодическими.

Визначення.

Неперіодичні десяткові дроби (або просто неперіодичні дроби) - це нескінченні десяткові дроби, що не мають періоду.

Іноді неперіодичні дроби мають вигляд, схожий з видом періодичних дробів, наприклад, +8,02002000200002 ... - неперіодичних дріб. У цих випадках слід бути особливо уважними, щоб помітити різницю.

Відзначимо, що неперіодичні дроби не перекладаються в звичайні дроби, нескінченні неперіодичні десяткові дроби представляють ірраціональні числа.

Дії з десятковими дробами

Одним з дій з десятковими дробами є порівняння, також визначені чотири основних арифметичних дії з десятковими дробами: Додавання, віднімання, множення і ділення. Розглянемо окремо кожне з дій з десятковими дробами.

Порівняння десяткових дробів по суті базується на порівнянні звичайних дробів, що відповідають порівнюваним десятковим дробям. Однак переклад десяткових дробів в звичайні є досить трудомістким процесом, та й нескінченні неперіодичні дроби не можуть бути представлені у вигляді звичайного дробу, тому зручно використовувати поразрядное порівняння десяткових дробів. Порозрядне порівняння десяткових дробів аналогічно порівнянні натуральних чисел. Для отримання більш детальної інформації рекомендуємо вивчити матеріал статті порівняння десяткових дробів, правила, приклади, рішення.

Переходимо до наступного кроку - множенню десяткових дробів. Множення кінцевих десяткових дробів проводиться аналогічно віднімання десяткових дробів, правила, приклади, рішення множенню стовпчиком натуральних чисел. У разі періодичних дробів множення можна звести до множення звичайних дробів. У свою чергу множення нескінченних неперіодичних десяткових дробів після їх округлення зводиться до множення кінцевих десяткових дробів. Рекомендуємо до подальшого вивчення матеріал статті множення десяткових дробів, правила, приклади, рішення.

Десяткові дроби на координатному промені

Між точками і десятковими дробами існує взаємно однозначна відповідність.

Розберемося, як будуються точки на координатному промені, відповідні даної десяткового дробу.

Кінцеві десяткові дроби і нескінченні періодичні десяткові дроби ми можемо замінити рівними їм звичайними дробами, після чого побудувати відповідні звичайні дроби на координатному промені. Наприклад, десяткового дробу 1,4 відповідає звичайна дріб 14/10, тому точка з координатою 1,4 віддалена від початку відліку в позитивному напрямку на 14 відрізків, рівних десятій частці одиничного відрізка.

Десяткові дроби можна відзначати на координатному промені, відштовхуючись від розкладання даної десяткового дробу за розрядами. Наприклад, нехай нам потрібно побудувати точку з координатою 16,3007, так як 16,3007 \u003d 16 + 0,3 + 0,0007, то в дану точку можна потрапити, послідовно відкладаючи від початку координат 16 одиничних відрізків, 3 відрізка, довжина яких дорівнює десятій частці одиничного, і 7 відрізків, довжина якого дорівнює десятитисячної частці одиничного відрізка.

Такий спосіб побудови десяткових чисел на координатному промені дозволяє як завгодно близько наблизитися до точки, що відповідає нескінченного десяткового дробу.

Іноді можливо точно побудувати точку, відповідну нескінченного десяткового дробу. наприклад, , Тоді цій нескінченній десяткового дробу 1,41421 ... відповідає точка координатного променя, віддалена від початку координат на довжину діагоналі квадрата зі стороною 1 одиничний інтервал.

Зворотний процес отримання десяткового дробу, відповідної даній точці на координатному промені, являє собою так зване десяткове вимір відрізка. Розберемося, як воно проводиться.

Нехай наша задача полягає в тому, щоб потрапити з початку відліку в дану точку координатної прямої (або нескінченно наблизитися до неї, якщо потрапити в неї не виходить). При десятковому вимірі відрізка ми можемо послідовно відкладати від початку відліку будь-яку кількість одиничних відрізків, далі відрізків, довжина яких дорівнює десятій частці одиничного, потім відрізків, довжина яких дорівнює сотій частці одиничного, і т.д. Записуючи кількість відкладених відрізків кожної довжини, ми отримаємо десяткову дріб, що відповідає даній точці на координатному промені.

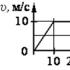
Наприклад, щоб потрапити в точку М на наведеному вище малюнку, потрібно відкласти 1 одиничний інтервал і 4 відрізка, довжина яких дорівнює десятій частці одиничного. Таким чином, точці М відповідає десяткова дріб 1,4.

Зрозуміло, що точкам координатного променя, в які неможливо потрапити в процесі десяткового вимірювання, відповідають нескінченні десяткові дроби.

Список літератури.

Математика: Навч. для 5 кл. загальноосвіт. установ / Н. Я. Віленкін, В. І. Жохов, А. С. Чесноков, С. І. Шварцбурд. - 21-е изд., Стер. - М .: Мнемозина, 2007. - 280 с .: іл. ISBN 5-346-00699-0.
Математика. 6 клас: навч. для загальноосвіт. установ / [Н. Я. Виленкин и др.]. - 22-е изд., Испр. - М .: Мнемозина, 2008. - 288 с .: іл. ISBN 978-5-346-00897-2.
алгебра: навч. для 8 кл. загальноосвіт. установ / [Ю. Н. Макаричєв, Н. Г. Миндюк, К. І. Нешков, С. Б. Суворова]; під ред. С. А. Теляковского. - 16-е изд. - М.: Просвещение, 2008. - 271 с. : Ил. - ISBN 978-5-09-019243-9.
Гусєв В. А., Мордкович А. Г. Математика (посібник для вступників до технікумів): Учеб. посібник.- М .; Вища. шк., 1984.-351 с., іл.

Як відомо, безліч раціональних чисел (Q) включає в себе безлічі цілих чисел (Z), яке в свою чергу включає безліч натуральних чисел (N). Крім цілих чисел в раціональні числа входять дробу.

Чому ж тоді все безліч раціональних чисел розглядають іноді як нескінченні десяткові періодичні дроби? Адже крім дробів, вони включають і цілі числа, а також неперіодичні дроби.

Справа в тому, що всі цілі числа, а також будь-яку дріб можна представити у вигляді нескінченного періодичного десяткового дробу. Тобто для всіх раціональних чисел можна використовувати однаковий спосіб запису.

Як видається нескінченний періодичний десятковий дріб? У ній повторюється групу цифр після коми беруть в дужки. Наприклад, 1,56 (12) - це дріб, у якої повторюється група цифр 12, т. Е. Дріб має значення +1,561212121212 ... і так без кінця. Періодична група цифр називається періодом.

Однак в подібному вигляді ми можемо уявити будь-яке число, якщо будемо вважати його періодом цифру 0, яка також повторюється без кінця. Наприклад, число 2 - це те ж саме, що 2,00000 .... Отже, його можна записати у вигляді нескінченного періодичного дробу, т. Е. 2, (0).

Те ж саме можна зробити і з будь-якої кінцевої дробом. наприклад:

0,125 = 0,1250000... = 0,125(0)

Однак на практиці не використовують перетворення кінцевої дробу в нескінченну періодичну. Тому поділяють кінцеві дроби і нескінченні періодичні. Таким чином, правильніше говорити, що до раціональних числах належать

всі цілі числа,
кінцеві дробу,
нескінченні періодичні дроби.

При цьому просто пам'ятають, що цілі числа і кінцеві дробу представимо в теорії у вигляді нескінченних періодичних дробів.

З іншого боку, поняття кінцевої і нескінченної дробу вживані до десятковим дробям. Якщо говорити про звичайних дробах, то як кінцеву, так і нескінченну десяткову дріб можна однозначно представити у вигляді звичайного дробу. Значить, з точки зору звичайних дробів, періодичні та кінцеві дроби - це одне і те ж. Крім того, цілі числа також можуть бути представлені у вигляді звичайного дробу, якщо уявити, що ми ділимо це число на 1.

Як уявити десяткову нескінченну періодичну дріб у вигляді звичайного? Найчастіше використовують приблизно такий алгоритм:

Призводять дріб до виду, щоб після коми виявився тільки період.
Множать нескінченну періодичну дріб на 10 або 100 або ... так, щоб кома пересунулася вправо на один період (т. Е. Один період виявився в цілій частині).
Прирівнюють вихідну дріб (a) змінної x, а отриману шляхом множення на число N дріб (b) - до Nx.
З Nx віднімають x. З b вичитав a. Т. е. Складають рівняння Nx - x \u003d b - a.
При вирішенні рівняння виходить звичайна дріб.

Приклад перекладу нескінченного періодичного десяткового дробу в звичайну дріб:
x \u003d 1,13333 ...
10x \u003d 11,3333 ...
10x * 10 \u003d 11,33333 ... * 10
100x \u003d 113,3333 ...
100x - 10x \u003d 113,3333 ... - 11,3333 ...
90x \u003d 102
x \u003d

Пам'ятайте, як в самому першому уроці про десяткові дроби я говорив, що існують числові дроби, що не представимо у вигляді десяткових (див. Урок «Десяткові дроби»)? Ми ще вчилися розкладати знаменники дробів на множники, щоб перевірити, чи немає там чисел, відмінних від 2 і 5.

Так ось: я набрехав. І сьогодні ми навчимося переводити абсолютно будь-яку числову дріб в десяткову. Заодно познайомимося з цілим класом дробів з нескінченної значущою частиною.

Періодична десяткова дріб - це будь-яка десяткова дріб, у якої:

Значуща частина складається з нескінченної кількості цифр;

Через певні інтервали цифри в значущої частини повторюються.

Набір цифр, що повторюються, з яких складається значуща частина, називається періодичною частиною дробу, а кількість цифр в цьому наборі - періодом дробу. Решта відрізок значущої частини, який не повторюється, називається неперіодичної частиною.

Оскільки визначень багато, варто докладно розглянути кілька таких дробів:

Ця дріб зустрічається в завданнях найчастіше. Неперіодичних частину: 0; періодична частина: 3; довжина періоду: 1.

Неперіодичних частину: 0,58; періодична частина: 3; довжина періоду: знову 1.

Неперіодичних частину: 1; періодична частина: 54; довжина періоду: 2.

Неперіодичних частину: 0; періодична частина: шістсот сорок одна тисяча двадцять п'ять; довжина періоду: 6. Для зручності повторювані частини відділені одна від одної пропуском - в цьому рішенні так робити не обов'язково.

Неперіодичних частину: 3066; періодична частина: 6; довжина періоду: 1.

Як бачите, визначення періодичної дробу засноване на понятті значущої частини числа. Тому якщо ви забули що це таке, рекомендую повторити - см. Урок «».

Перехід до періодичного десяткового дробу

Розглянемо звичайну дріб виду a / b. Розкладемо її знаменник на прості множники. Можливі два варіанти:

У розкладанні присутні тільки множники 2 і 5. Ці дробу легко приводяться до десятковим - см. Урок «Десяткові дроби». Такі нас не цікавлять;
У розкладанні є щось ще, крім 2 і 5. У цьому випадку дріб непредставима у вигляді десяткового, зате з неї можна зробити періодичну десяткову дріб.

Щоб задати періодичну десяткову дріб, треба знайти її періодичну і неперіодичних частину. Як? Переведіть дріб в неправильну, а потім розділіть чисельник на знаменник «куточком».

При цьому буде відбуватися наступне:

спочатку розділиться ціла частина, Якщо вона є;
Можливо, буде кілька чисел після десяткового дробу;
Через деякий час цифри почнуть повторюватися.

От і все! Повторювані цифри після десяткового дробу позначаємо періодичної частиною, а то, що стоїть попереду - неперіодичної.

Завдання. Переведіть звичайні дроби в періодичні десяткові:

Все дробу без цілої частини, тому просто ділимо чисельник на знаменник «куточком»:

Як бачимо, залишки повторюються. Запишемо дріб в «правильному» вигляді: 1,733 ... \u003d 1,7 (3).

У підсумку виходить дріб: 0,5833 ... \u003d 0,58 (3).

Записуємо в нормальному вигляді: 4,0909 ... \u003d 4, (09).

Отримуємо дріб: 0,4141 ... \u003d 0, (41).

Перехід від періодичного десяткового дробу до звичайної

Розглянемо періодичну десяткову дріб X \u003d abc (a 1 b 1 c 1). Потрібно перевести її в класичну «двоповерхову». Для цього виконаємо чотири простих кроки:

Знайдіть період дробу, тобто підрахуйте, скільки цифр знаходиться в періодичній частини. Нехай це буде число k;
Знайдіть значення виразу X · 10 k. Це рівносильно зрушення десяткового дробу на повний період вправо - см. Урок «Множення і ділення десяткових дробів»;
З отриманого числа треба відняти початкове вираз. При цьому періодична частина «спалюється», і залишається звичайна дріб;
В отриманому рівнянні знайти X. Все десяткові дроби переводимо в звичайні.

Завдання. Наведіть до звичайної неправильного дробу числа:

9,(6);
32,(39);
0,30(5);
0,(2475).

Працюємо з першої дробом: X \u003d 9, (6) \u003d 9,666 ...

У дужках міститься лише одна цифра, тому період k \u003d 1. Далі множимо цю дріб на 10 k \u003d 10 +1 \u003d 10. Маємо:

10X \u003d 10 · 9,6666 ... \u003d 96,666 ...

Віднімаємо вихідну дріб і вирішуємо рівняння:

10X - X \u003d 96,666 ... - 9,666 ... \u003d 96 - 9 \u003d 87;
9X \u003d 87;
X \u003d 87/9 \u003d 29/3.

Тепер розберемося з другої дробом. Отже, X \u003d 32, (39) \u003d 32,393939 ...

Період k \u003d 2, тому множимо всі на 10 k \u003d 10 2 \u003d 100:

100X \u003d 100 · 32,393939 ... \u003d 3239,3939 ...

Знову віднімаємо вихідну дріб і вирішуємо рівняння:

100X - X \u003d 3239,3939 ... - 32,3939 ... \u003d 3239 - 32 \u003d 3207;
99X \u003d 3207;
X \u003d 3207/99 \u003d 1069/33.

Приступаємо до третьої дробу: X \u003d 0,30 (5) \u003d 0,30555 ... Схема та ж сама, тому я просто наведу викладки:

Період k \u003d 1 ⇒ множимо всі на 10 k \u003d 10 1 \u003d 10;

10X \u003d 10 · 0,30555 ... \u003d 3,05555 ...
10X - X \u003d 3,0555 ... - 0,305555 ... \u003d 2,75 \u003d 11/4;
9X \u003d 11/4;
X \u003d (11/4): 9 \u003d 11/36.

Нарешті, остання дріб: X \u003d 0, (2475) \u003d 0,2475 2475 ... Знову ж таки, для зручності періодичні частини відокремлені один від одного пробілами. маємо:

k \u003d 4 ⇒ 10 k \u003d 10 4 \u003d 10 000;
10 000X \u003d 10 000 · 0,2475 2475 \u003d 2475,2475 ...
10 000X - X \u003d 2475,2475 ... - 0,2475 2475 ... \u003d 2475;
9999X \u003d 2475;
X \u003d 2475: 9999 \u003d 25/101.

Що якщо вони знають теорію рядів, то значить без неї ніяких метаматіческіх понять вводити не можна. Більш того, ці люди вважають, що той, хто не скористався повсюдно, - невіглас. Залишимо погляди цих людей на їх совісті. Давайте краще розберемося з тим, що таке нескінченний періодичний дріб і як з нею бути нам, неосвіченим людям, які не знають меж.

Поділимо 237 на 5. Ні, не потрібно запускати «Калькулятор». Давайте краще згадаємо середню (або навіть початкову?) Школу і просто поділимо стовпчиком:

Ну як, згадали? Тоді можна і до справи переходити.

Поняття «дріб» в математиці має два значення:

Нецілим число.
Форма запису нецілого числа.

Існує два види дробів - в сенсі, дві форми запису нецілих чисел:

Прості (або вертикальні) Дроби, на кшталт 1/2 або 237/5.
Десяткові дроби, наприклад, 0,5 або 47,4.

Зауважимо, що взагалі само використання дробу-записи не означає, що записане є дріб-число, наприклад 3/3 або 7,0 - НЕ дробу в першому сенсі слова, але в другому, звичайно, дробу.

В математиці, взагалі споконвіку прийнято рахунок десятковий, а тому і десяткові дроби зручніше простих, т. Е. Дріб з десятковим знаменником (Володимир Даль. Тлумачний словник живої великоросійської мови. «Десять»).

А раз так, то хочеться всяку дріб вертикальну зробити десяткового ( «горизонтальної»). А для цього потрібно просто-напросто чисельник поділити на знаменник. Візьмемо, наприклад, дріб 1/3 і спробуємо зробити з неї десяткову.

Навіть зовсім неосвічений помітить: скільки не діли - не розділені: так і будуть трійки до нескінченності з'являтися. Так і запишемо: 0,33 ... Маємо на увазі при цьому «число, яке виходить, коли ділиш 1 на 3», або, коротше, «одна третя». Природно, що одна третя - дріб в першому сенсі слова, а «1/3» і «0,33 ...» - дроби в другому сенсі слова, тобто форми запису числа, яке знаходиться на числової прямої на такій відстані від нуля, що якщо тричі його відкласти, вийде одиниця.

Тепер спробуємо розділити 5 на 6:

Знову запишемо: 0,833 ... Маємо на увазі «число, яке виходить, коли ділиш 5 на 6», або, коротше, «п'ять шостих». Однак, тут виникає плутанина: чи мається на увазі 0,83333 (і далі трійки повторюються), або ж 0,833833 (і далі 833 повторюється). Тому запис з трьома крапками нас не влаштовує: незрозуміло, звідки починається повтряющаяся частина (вона називається «період»). Тому період ми будемо брати в дужки, ось так: 0, (3); 0,8 (3).

0, (3) не просто одно однієї третьої, це є одна третя, адже ми спеціально цей запис придумали, щоб представляти це число у вигляді десяткового дробу.

Ця запис і називається нескінченного періодичного дробом, Або просто періодичної дробом.

Завжди, коли ми ділимо одне число на інше, якщо не виходить дріб кінцева, то виходить дріб нескінченний періодичний, тобто обов'язково коли-небудь послідовності цифр почнуть повторюватися. Чому це так можна зрозуміти чисто умоглядно, подивившись уважно на алгоритм ділення стовпчиком:

У місцях, позначених галочками, не можуть весь час виходити різні пари чисел (тому, що таких пар в принципі кінцеве безліч). А як тільки там з'явиться така пара, яка вже була, різниця теж буде такою ж - і далі весь процес почне повторюватися. Немає потреби перевіряти це, адже цілком очевидно, що при повторенні тих самих дій результати будуть ті ж.

Тепер, коли ми добре розуміємо суть періодичної дробу, давайте спробуємо помножити одну третину на три. Так, вийде, звичайно, один, але давайте запишемо цю дріб в десяткового формі і помножимо стовпчиком (двусмисліци через крапки тут не виникає, так як всі цифри після коми однакові):

І знову ми помічаємо, що весь час будуть після коми з'являтися дев'ятки, дев'ятки і дев'ятки. Тобто, використовуючи, назад, дужкову запис, ми отримаємо 0, (9). Оскільки ми знаємо, що твір однієї третини і трьох є одиниця, то 0, (9) - це така ось химерна форма запису одиниці. Однак використовувати таку форму запису недоцільно, адже одиниця прекрасно записується і без використання періоду, ось так: 1.

Як бачимо, 0, (9) - це один з тих випадків, коли ціле число записано в формі дробу, начебто 3/3 або 7,0. Тобто, 0, (9) - це дріб лише в другому сенсі слова, але ніяк не в першому.

Ось так, без жодних меж і рядів ми розібралися з тим, що таке 0, (9) і як з ним боротися.

Але все ж згадаємо про те, що на самій-то справі ми розумні і вивчали аналіз. Дійсно, важко заперечувати, що:

Але, мабуть, ніхто не буде сперечатися і з тим, що:

Все це, звичайно, вірно. Дійсно, 0, (9) є і сумою наведеного ряду, і подвоєним синусом зазначеного кута, і натуральним логарифмом числа Ейлера.

Але ні те, ні інше, ні третє не є визначенням.

Стверджувати, що 0, (9) - сума нескінченної низки 9 / (10 n), при n від одиниці, - це все одно, що стверджувати, що синус - це сума нескінченної низки Тейлора:

це абсолютно вірно, І це є найважливішим фактом для обчислювальної математики, Але це не визначення, і, що найголовніше, це нітрохи не наближає людину до розуміння суті синуса. Суть же синуса деякого кута полягає в тому, що це всього-навсього відношення протилежного кутку катета до гіпотенузи.

Дак от, періодична дріб - це всього-навсього десяткова дріб, яка виходить, коли при розподілі стовпчиком один і той же набір цифр повторется. Аналізу тут немає і в помині.

І ось тут-то виникає питання: звідки взагалі ми взяли число 0, (9)? Що на що ми ділимо стовпчиком, щоб його отримати? Дійсно, немає таких чисел, при розподілі яких один на одного стовпчиком ми б мали нескінченно з'являються дев'ятки. Але нам таки вдалося отримати це число, множачи стовпчиком 0, (3) на 3? Не зовсім. Адже множити потрібно справа наліво, щоб коректно враховувати перенесення розрядів, а ми це робили зліва направо, хитро скориставшись тим, що приносив ніде все одно не виникає. Тому правомірність записи 0, (9) залежить від того, визнаємо ми правомірність такого множення стовпчиком чи ні.

Отже, можна взагалі сказати, що запис 0, (9) некоректна - і в певній мірі бути правим. Однак, оскільки нотація a, (b) прийнята, то просто негарно відмовлятися від неї при b \u003d 9; краще визначитися з тим, що такий запис означає. Так що, якщо ми взагалі приймаємо запис 0, (9), то цей запис, звичайно, означає число один.

Залишилося лише додати, що якби ми використовували, скажімо, трійкову систему числення, то при розподілі стовпчиком одиниці (1 3) на трійку (10 3) вийшло б 0,1 3 (читається «нуль цілих одна третя»), а при діленні одиниці на двійку вийшло б 0, (1) 3.

Так що періодичність дроби-записи - це не об'єктивна якась характеристика дроби-числа, а всього лише побічний ефект використання тієї чи іншої системи числення.