Barcha qo'shimcha formulalar. Asosiy trigonometriya formulalari

Qo'shish formulalari a va b burchaklarining sinuslari va kosinuslari, cos (a + b), cos (a-b), sin (a + b), sin (a-b) funktsiyalarining qiymatlarini ifodalash uchun ishlatiladi.

Sinuslar va kosinuslar uchun qo'shimcha formulalar

Teorema: Har qanday a va b uchun quyidagi tenglik rost cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).

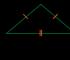
Keling, bu teoremani isbotlaylik. Quyidagi rasmni ko'rib chiqing:

Unda Mo nuqtani mos ravishda a, -b va a+b burchaklar orqali aylantirib Ma, M-b, M(a+b) nuqtalar olinadi. Sinus va kosinus taʼriflaridan bu nuqtalarning koordinatalari quyidagicha boʻladi: Ma(cos(a); sin(a)), Mb (cos(-b); sin(-b)), M(a+). b) (cos(a+ b);sin(a+b)). MoOM burchagi (a + b) \u003d M-bOM burchagi, shuning uchun MoOM (a + b) va M-bOM uchburchaklari teng va ular teng yonlidir. Demak, MoM (a-b) va M-bMa asoslari ham teng. Shuning uchun (MoM(a-b))^2 = (M-bMa)^2. Ikki nuqta orasidagi masofa formulasidan foydalanib, biz quyidagilarni olamiz:

(1 - cos(a+b))^2 + (sin(a+b))^2 = (cos(-b) - cos(a))^2 + (sin(-b) - sin(a) )^2.

sin(-a) = -sin(a) va cos(-a) = cos(a). Keling, ushbu formulalarni va yig'indi va ayirma kvadratini hisobga olgan holda tengligimizni o'zgartiramiz, keyin:

1 -2*cos(a+b) + (cos(a+b))^2 +(sin(a+b))^2 = (cos(b))^2 - 2*cos(b)*cos (a) + (cos(a)^2 +(sin(b))^2 +2*sin(b)*sin(a) + (sin(a))^2.

Endi biz asosiy trigonometrik identifikatsiyani qo'llaymiz:

2-2*cos(a+b) = 2 - 2*cos(a)*cos(b) + 2*sin(a)*sin(b).

Biz shunga o'xshashlarni beramiz va -2 ga kamaytiramiz:

cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b). Q.E.D.

Quyidagi formulalar ham amal qiladi:

cos(a-b) = cos(a)*cos(b) + sin(a)*sin(b);
sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b);
sin(a-b) = sin(a)*cos(b) - cos(a)*sin(b).

Bu formulalarni yuqorida isbotlanganidan, kamaytirish formulalari yordamida va b ni -b bilan almashtirib olish mumkin. Tangens va kotangentlar uchun qo'shish formulalari ham mavjud, ammo ular hech qanday argumentlar uchun haqiqiy bo'lmaydi.

Tangens va kotangens qo‘shish formulalari

Har qanday uchun burchaklar a, b a=pi/2+pi*k, b=pi/2 +pi*n va a+b =pi/2 +pi*m bundan mustasno, har qanday uchun k,n,m butun sonlar quyidagi formula amal qiladi:

tg(a+b) = (tg(a) + tg(b))/(1-tg(a)*tg(b)).

a=pi/2+pi*k, b=pi/2 +pi*n va ab =pi/2 +pi*m bundan mustasno a,b burchaklari uchun k,n,m butun sonlar uchun quyidagi formula amal qiladi. :

tg(a-b) = (tg(a)-tg(b))/(1+tg(a)*tg(b)).

a=pi*k, b=pi*n, a+b = pi*m bundan mustasno har qanday a,b burchaklar uchun va k,n,m butun sonlar uchun quyidagi formula to‘g‘ri bo‘ladi:

ctg(a+b) = (ctg(a)*ctg(b) -1)/(ctg(b)+ctg(a)).

Asosiy trigonometrik funktsiyalar - sinus, kosinus, tangens va kotangens o'rtasidagi nisbatlar berilgan. trigonometrik formulalar. Va trigonometrik funktsiyalar o'rtasida juda ko'p bog'lanishlar mavjudligi sababli, bu trigonometrik formulalarning ko'pligini ham tushuntiradi. Ba'zi formulalar bir xil burchakning trigonometrik funktsiyalarini bog'laydi, boshqalari - ko'p burchakning funktsiyalari, boshqalari - darajani kamaytirishga imkon beradi, to'rtinchisi - barcha funktsiyalarni yarim burchakning tangensi orqali ifodalash va hokazo.

Ushbu maqolada biz trigonometriya muammolarining katta qismini hal qilish uchun etarli bo'lgan barcha asosiy trigonometrik formulalarni tartib bilan sanab o'tamiz. Yodlash va foydalanish qulayligi uchun biz ularni maqsadlariga ko'ra guruhlarga ajratamiz va jadvallarga kiritamiz.

Sahifani navigatsiya qilish.

Asosiy trigonometrik identifikatsiyalar

Asosiy trigonometrik identifikatsiyalar bir burchakning sinusi, kosinusu, tangensi va kotangensi o'rtasidagi munosabatni o'rnating. Ular sinus, kosinus, tangens va kotangensning ta'rifidan, shuningdek, birlik doirasi tushunchasidan kelib chiqadi. Ular bir trigonometrik funktsiyani boshqasi orqali ifodalash imkonini beradi.

Ushbu trigonometriya formulalarining batafsil tavsifi, ularni olish va qo'llash misollari uchun maqolaga qarang.

Shakllangan formulalar

Shakllangan formulalar sinus, kosinus, tangens va kotangens xossalaridan kelib chiqadi, ya'ni ular trigonometrik funksiyalarning davriylik xususiyatini, simmetriya xossasini, shuningdek, berilgan burchakka siljish xossalarini aks ettiradi. Ushbu trigonometrik formulalar ixtiyoriy burchaklar bilan ishlashdan noldan 90 gradusgacha bo'lgan burchaklar bilan ishlashga o'tishga imkon beradi.

Ushbu formulalarning mantiqiy asoslari, ularni yodlashning mnemonik qoidasi va ularni qo'llash misollari maqolada o'rganilishi mumkin.

Qo'shimcha formulalar

Trigonometrik qo'shish formulalari Ikki burchak yig‘indisining yoki ayirmasining trigonometrik funksiyalari shu burchaklarning trigonometrik funksiyalari bilan qanday ifodalanishini ko‘rsating. Bu formulalar quyidagi trigonometrik formulalarni chiqarish uchun asos bo'lib xizmat qiladi.

Ikki, uch va boshqalar uchun formulalar. burchak

Ikki, uch va boshqalar uchun formulalar. burchak (ular ko'p burchak formulalari deb ham ataladi) ikki, uch va boshqalarning trigonometrik funktsiyalarini ko'rsatadi. burchaklar () bitta burchakning trigonometrik funktsiyalari bilan ifodalanadi. Ularning hosilasi qo'shish formulalariga asoslanadi.

Batafsil ma'lumot ikki, uch va boshqalar uchun maqola formulalarida to'plangan. burchak.

Yarim burchak formulalari

Yarim burchak formulalari yarim burchakning trigonometrik funktsiyalari butun burchakning kosinusida qanday ifodalanishini ko'rsating. Bu trigonometrik formulalar ikki burchakli formulalardan kelib chiqadi.

Ularning xulosasi va qo'llash misollarini maqolada topish mumkin.

Qisqartirish formulalari

Darajani kamaytirish uchun trigonometrik formulalar trigonometrik funktsiyalarning tabiiy kuchlaridan birinchi darajali sinuslar va kosinuslarga o'tishni osonlashtirish uchun mo'ljallangan, lekin bir nechta burchaklar. Boshqacha qilib aytganda, ular trigonometrik funktsiyalarning kuchlarini birinchi darajaga kamaytirishga imkon beradi.

Trigonometrik funksiyalarning yig‘indisi va ayirmasining formulalari

Asosiy maqsad trigonometrik funksiyalar uchun yig‘indi va ayirma formulalari funksiyalar mahsulotiga o'tishdan iborat bo'lib, bu trigonometrik ifodalarni soddalashtirishda juda foydali. Bu formulalardan yechishda ham keng foydalaniladi trigonometrik tenglamalar, chunki ular sinus va kosinuslarning yig'indisi va farqini faktoringga ajratish imkonini beradi.

Sinuslar, kosinuslar va sinuslarning kosinus bo'yicha ko'paytmasi uchun formulalar

Trigonometrik funksiyalarning ko`paytmasidan yig`indiga yoki ayirmaga o`tish sinuslar, kosinuslar va sinuslarning kosinuslar ko`paytmasi formulalari orqali amalga oshiriladi.

Universal trigonometrik almashtirish

Trigonometriyaning asosiy formulalarini ko'rib chiqishni trigonometrik funktsiyalarni yarim burchakning tangensi bo'yicha ifodalovchi formulalar bilan yakunlaymiz. Bu almashtirish deyiladi universal trigonometrik almashtirish. Uning qulayligi shundan iboratki, barcha trigonometrik funktsiyalar ildizlarsiz ratsional ravishda yarim burchakning tangensi bilan ifodalanadi.

Adabiyotlar ro'yxati.

Algebra: Proc. 9 hujayra uchun. o'rtacha maktab / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovskiy.- M.: Ma'rifat, 1990.- 272 b.: Ill.- ISBN 5-09-002727-7
Bashmakov M.I. Algebra va tahlilning boshlanishi: Proc. 10-11 hujayra uchun. o'rtacha maktab - 3-nashr. - M.: Ma'rifat, 1993. - 351 b.: kasal. - ISBN 5-09-004617-4.
Algebra va tahlilning boshlanishi: Proc. 10-11 hujayra uchun. umumiy ta'lim muassasalar / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn va boshqalar; Ed. A. N. Kolmogorova.- 14-nashr.- M.: Ma'rifat, 2004.- 384 b.: ill.- ISBN 5-09-013651-3.
Gusev V. A., Mordkovich A. G. Matematika (texnika maktablariga abituriyentlar uchun qo'llanma): Proc. nafaqa.- M.; Yuqori maktab, 1984.-351 b., kasal.

Aqlli talabalar tomonidan mualliflik huquqi

Barcha huquqlar himoyalangan.
Mualliflik huquqi qonuni bilan himoyalangan. Saytning biron bir qismi, shu jumladan ichki materiallar va tashqi dizayn, mualliflik huquqi egasining yozma ruxsatisiz har qanday shaklda ko'paytirilishi yoki ishlatilishi mumkin emas.

Men sizni aldash varaqlarini yozmaslikka ishontirmayman. Yozing! Trigonometriya bo'yicha cheat varaqlari, shu jumladan. Keyinchalik men cheat varaqlari nima uchun kerakligini va qanday qilib foydali ekanligini tushuntirishni rejalashtirmoqdaman. Va bu erda - qanday qilib o'rganmaslik haqida ma'lumot, lekin ba'zi trigonometrik formulalarni eslab qolish. Shunday qilib, trigonometriya varaqsiz! Biz yodlash uchun assotsiatsiyalardan foydalanamiz.

1. Qo‘shish formulalari:

kosinuslar har doim "juft bo'lib ketadi": kosinus-kosinus, sinus-sinus. Va yana bir narsa: kosinuslar "etarsiz". Ular "hamma narsa noto'g'ri", shuning uchun ular belgilarni o'zgartiradilar: "-" ni "+" ga va aksincha.

Sinuslar - "aralash": sinus-kosinus, kosinus-sinus.

2. Yig‘indi va ayirma formulalari:

kosinuslar har doim "juft bo'lib ketadi". Ikkita kosinus - "bulochka" qo'shib, biz bir juft kosinus - "koloboks" ni olamiz. Va ayirish, biz, albatta, koloboklarni olmaymiz. Biz bir nechta sinuslarni olamiz. Oldinda hali minus.

Sinuslar - "aralash" :

3. Ko`paytmani yig`indiga va ayirmaga aylantirish formulalari.

Biz qachon bir juft kosinus olamiz? Kosinuslarni qo'shganda. Shunday qilib

Qachon biz bir juft sinusni olamiz? Kosinuslarni ayirishda. Bu yerdan:

"Aralash" sinuslarni qo'shish va ayirish yo'li bilan olinadi. Qaysi biri qiziqroq: qo'shish yoki ayirish? To'g'ri, katlayın. Va formula uchun qo'shimchani oling:

Qavslar ichidagi birinchi va uchinchi formulalarda - miqdori. Atamalar joylarini qayta tartibga solishdan yig'indi o'zgarmaydi. Buyurtma faqat ikkinchi formula uchun muhimdir. Ammo, chalkashmaslik uchun, eslab qolish qulayligi uchun, birinchi qavsdagi barcha uchta formulada biz farqni olamiz.

ikkinchidan, summa

Cho'ntagingizdagi beshik choyshablari xotirjamlik beradi: formulani unutib qo'ysangiz, uni yozib qo'yishingiz mumkin. Va ular ishonch bag'ishlaydi: agar siz cheat varag'idan foydalanmasangiz, formulalarni osongina eslab qolishingiz mumkin.

Biz trigonometriyada eng ko'p ishlatiladigan formulalar haqida suhbatimizni davom ettiramiz. Ulardan eng muhimi qo'shish formulalaridir.

Ta'rif 1

Qo'shish formulalari bu burchaklarning trigonometrik funktsiyalaridan foydalangan holda farqning funktsiyalarini yoki ikki burchak yig'indisini ifodalash imkonini beradi.

Boshlash uchun biz qo'shish formulalarining to'liq ro'yxatini beramiz, keyin ularni isbotlaymiz va ba'zi illyustrativ misollarni tahlil qilamiz.

Yandex.RTB R-A-339285-1

Trigonometriyada asosiy qo‘shish formulalari

Sakkizta asosiy formula mavjud: yig'indining sinusi va ikki burchak ayirmasining sinusi, yig'indi va ayirmaning kosinuslari, yig'indi va ayirmaning tangenslari va kotangentlari. Quyida ularning standart formulalari va hisob-kitoblari keltirilgan.

1. Ikki burchak yig‘indisining sinusini quyidagicha olish mumkin:

Birinchi burchak sinusining ko'paytmasini ikkinchisining kosinusiga hisoblaymiz;

Birinchi burchakning kosinusini birinchi burchakning sinusiga ko'paytiring;

Olingan qiymatlarni qo'shing.

Formulaning grafik yozilishi quyidagicha ko'rinadi: sin (a + b) = sin a cos b + cos a sin b.

2. Farqning sinusi deyarli bir xil tarzda hisoblanadi, faqat natijada olingan mahsulotlar qo'shilmasligi kerak, lekin bir-biridan ayiriladi. Shunday qilib, birinchi burchak sinusining ikkinchisining kosinusiga va birinchi burchakning kosinusining ikkinchisining sinusiga ko'paytmalarini hisoblaymiz va ularning farqini topamiz. Formula shunday yoziladi: sin (a - b) = sin a cos b + sin a sin b.

3. Yig‘indining kosinusu. Buning uchun mos ravishda birinchi burchak kosinusining ikkinchisining kosinusiga va birinchi burchak sinusining ikkinchisining sinusiga koʻpaytmalarini topamiz va ularning farqini topamiz: cos (a + b) = cos a. cos b - sin a sin b

4. Kosinuslar farqi: berilgan burchaklarning sinuslari va kosinuslarining ko’paytmalarini avvalgidek hisoblab chiqamiz va qo’shamiz. Formula: cos (a - b) = cos a cos b + sin a sin b

5. Yig‘indining tangensi. Bu formula kasr sifatida ifodalanadi, uning numeratorida kerakli burchaklar tangenslarining yig'indisi, maxrajda esa kerakli burchaklar tangenslarining ko'paytmasi ayiriladi. Uning grafik yozuvidan hamma narsa aniq: t g (a + b) = t g a + t g b 1 - t g a t g b

6. Farqning tangensi. Biz farqning qiymatlarini va bu burchaklarning tangenslari mahsulotini hisoblaymiz va ular bilan shunga o'xshash tarzda ishlaymiz. Maxrajda bittaga qo‘shamiz, aksincha emas: t g (a - b) = t g a - t g b 1 + t g a t g b.

7. Yig‘indining kotangensi. Ushbu formuladan foydalangan holda hisob-kitoblar uchun bizga ushbu burchaklarning kotangentlarining ko'paytmasi va yig'indisi kerak bo'lib, biz quyidagicha harakat qilamiz: c t g (a + b) = - 1 + c t g a c t g b c t g a + c t g b.

8. Farq kotangensi . Formula avvalgisiga o'xshaydi, lekin pay va maxrajda - minus va ortiqcha emas c t g (a - b) = - 1 - c t g a c t g b c t g a - c t g b.

Ehtimol, siz ushbu formulalar juftlik bilan o'xshashligini payqadingiz. ± (ortiqcha-minus) va ∓ (minus-plyus) belgilaridan foydalanib, biz ularni belgilash qulayligi uchun guruhlashimiz mumkin:

sin (a ± b) = sin a cos b ± cos a sin b cos (a ± b) = cos a cos b ∓ sin a sin b tg (a ± b) = tg a ± tg b 1 ∓ tg a tg. ctg (a ± b) = - 1 ± ctg a ctg b ctg a ± ctg b

Shunga ko'ra, bizda har bir qiymatning yig'indisi va farqi uchun bitta ro'yxatga olish formulasi mavjud, faqat bitta holatda biz yuqori belgiga, ikkinchisida - pastki belgiga e'tibor beramiz.

Ta'rif 2

Biz har qanday a va b burchaklarni olishimiz mumkin va kosinus va sinus uchun qo'shish formulalari ular uchun ishlaydi. Agar biz bu burchaklarning tangenslari va kotangenslarining qiymatlarini to'g'ri aniqlay olsak, ular uchun tangens va kotangens uchun qo'shimcha formulalar ham tegishli bo'ladi.

Algebradagi ko'pgina tushunchalar singari, qo'shish formulalari ham isbotlanishi mumkin. Biz isbotlaydigan birinchi formula - bu farq kosinus formulasi. Undan keyin qolgan dalillarni osongina chiqarib olishingiz mumkin.

Keling, asosiy tushunchalarni aniqlaylik. Bizga kerak bo'ladi birlik doirasi. Agar ma'lum bir A nuqtani olib, markaz (O nuqta) atrofida a va b burchaklarni aylantirsak, shunday bo'ladi. U holda O A 1 → va O A → 2 vektorlari orasidagi burchak (a - b) + 2 p z yoki 2 p - (a - b) + 2 p z ga teng bo'ladi (z har qanday butun son). Olingan vektorlar a - b yoki 2 p - (a - b) ga teng burchak hosil qiladi yoki bu qiymatlardan to'liq aylanishlarning butun soni bilan farq qilishi mumkin. Rasmga qarang:

Biz qisqartirish formulalaridan foydalandik va quyidagi natijalarga erishdik:

cos ((a - b) + 2 p z) = cos (a - b) cos (2 p - (a - b) + 2 p z) = cos (a - b)

Xulosa: O A 1 → va O A 2 → vektorlari orasidagi burchakning kosinasi a - b burchakning kosinusiga teng, shuning uchun cos (O A 1 → O A 2 →) = cos (a - b) .

Sinus va kosinusning ta'riflarini eslang: sinus - qarama-qarshi burchakning oyog'ining gipotenuzaga nisbatiga teng burchak funktsiyasi, kosinus - qo'shimcha burchakning sinusi. Shuning uchun, nuqtalar A 1 va A2 koordinatalariga ega (cos a , sin a ) va (cos b , sin b ) .

Biz quyidagilarni olamiz:

O A 1 → = (cos a , sin a) va O A 2 → = (cos b , sin b)

Agar aniq bo'lmasa, vektorlarning boshida va oxirida joylashgan nuqtalarning koordinatalariga qarang.

Vektorlarning uzunliklari 1 ga teng, chunki bizda bitta doira bor.

Endi tahlil qilaylik skalyar mahsulot O A 1 → va O A 2 → vektorlari. Koordinatalarda u quyidagicha ko'rinadi:

(O A 1 → , O A 2) → = cos a cos b + sin a sin b

Bundan biz tenglikni chiqarishimiz mumkin:

cos (a - b) = cos a cos b + sin a sin b

Shunday qilib, farqning kosinus formulasi isbotlangan.

Endi biz quyidagi formulani - yig'indining kosinusini isbotlaymiz. Bu osonroq, chunki biz oldingi hisob-kitoblardan foydalanishimiz mumkin. a + b = a - (- b) tasvirini oling. Bizda bor:

cos (a + b) = cos (a - (- b)) = = cos a cos (- b) + sin a sin (- b) = = cos a cos b + sin a sin b

Bu yig'indining kosinus formulasining isbotidir. Oxirgi qatorda qarama-qarshi burchaklarning sinusi va kosinuslari xossasi qo'llaniladi.

Yig'indining sinusi formulasini farqning kosinus formulasidan olish mumkin. Buning uchun kamaytirish formulasini olaylik:

shaklining sin (a + b) = cos (p 2 (a + b)) . Shunday qilib
sin (a + b) \u003d cos (p 2 (a + b)) \u003d cos ((p 2 - a) - b) \u003d \u003d cos (p 2 - a) cos b + sin (p 2 -) a) sin b = = sin a cos b + cos a sin b

Mana farqning sinusi formulasining isboti:

sin (a - b) = sin (a + (- b)) = sin a cos (- b) + cos a sin (- b) = = sin a cos b - cos a sin b.
Oxirgi hisoblashda qarama-qarshi burchaklarning sinus va kosinus xususiyatlaridan foydalanishga e'tibor bering.

Keyinchalik, bizga tangens va kotangens uchun qo'shish formulalarini isbotlash kerak. Keling, asosiy ta'riflarni eslaylik (tangent - sinusning kosinusga nisbati va kotangent aksincha) va oldindan olingan formulalarni olamiz. Biz buni qildik:

t g (a + b) = sin (a + b) cos (a + b) = sin a cos b + cos a sin b cos a cos b - sin a sin b.

Bizda murakkab kasr bor. Keyinchalik, uning soni va maxrajini cos a cos b ga bo'lishimiz kerak, cos a ≠ 0 va cos b ≠ 0 ekanligini hisobga olsak, biz quyidagilarni olamiz:
sin a cos b + cos a sin b cos a cos b cos a cos b - sin a sin b cos a cos b = sin a cos b cos a cos b + cos a sin b cos a cos b cos a cos b cos a cos b cos a cos b cos b - sin a sin b cos a cos b

Endi kasrlarni kamaytiramiz va quyidagi ko rinishdagi formulani olamiz: sin a cos a + sin b cos b 1 - sin a cos a s i n b cos b = t g a + t g b 1 - t g a t g b.
Biz t g (a + b) = t g a + t g b 1 - t g a · t g b ni oldik. Bu tangens qo'shish formulasining isbotidir.

Biz isbotlaydigan keyingi formula bu farqning tangens formulasidir. Hisob-kitoblarda hamma narsa aniq ko'rsatilgan:

t g (a - b) = t g (a + (- b)) = t g a + t g (- b) 1 - t g a t g (- b) = t g a - t g b 1 + t g a t g b

Kotangent formulalari xuddi shunday isbotlangan:
ctg (a + b) = cos (a + b) sin (a + b) = cos a cos b - sin a sin b sin a cos b + cos a sin b = = cos a cos b - sin a sin b sin. a sin b sin a cos b + cos a sin b sin a sin b = cos a cos b sin a sin b - 1 sin a cos b sin a sin b + cos a sin b sin a sin b = = - 1 + ctg. a ctg b ctg a + ctg b
Yana:
c t g (a - b) = c t g (a + (- b)) = - 1 + c t g a c t g (- b) c t g a + c t g (- b) = - 1 - c t g a c t g b c t g a - c t g