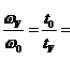Birinchi daraja

Arifmetik progressiya. Batafsil nazariya misollar bilan (2019)

Raqamli ketma-ketlik

Keling, o'tirib, bir nechta raqamlarni yozishni boshlaylik. Masalan:
Siz har qanday raqamlarni yozishingiz mumkin va ular xohlagancha ko'p bo'lishi mumkin (bizning holatlarimizda ular). Biz qancha son yozmaylik, ularning qaysi biri birinchi, qaysi biri ikkinchi ekanligini va shunga o'xshash oxirgisini aytishimiz mumkin, ya'ni ularni raqamlashimiz mumkin. Bu raqamlar ketma-ketligiga misol:

Raqamli ketma-ketlik
Masalan, bizning ketma-ketligimiz uchun:

Belgilangan raqam faqat bitta tartib raqamiga xosdir. Boshqacha qilib aytganda, ketma-ketlikda uchta ikkinchi raqam yo'q. Ikkinchi raqam (-chi raqam kabi) har doim bir xil bo'ladi.
Raqamli son qatorning --chi a'zosi deyiladi.

Biz odatda butun ketma-ketlikni qandaydir harf deb ataymiz (masalan,), va bu ketma-ketlikning har bir a'zosi - bu a'zoning soniga teng indeksli bir xil harf: .

Bizning holatda:

Aytaylik, bizda qo'shni sonlar orasidagi farq bir xil va teng bo'lgan sonli ketma-ketlik mavjud.
Masalan:

va hokazo.
Bunday sonli ketma-ketlik arifmetik progressiya deyiladi.
“Progressiya” atamasi 6-asrdayoq Rim muallifi Boethius tomonidan kiritilgan va kengroq maʼnoda cheksiz sonli ketma-ketlik sifatida tushunilgan. "Arifmetika" nomi qadimgi yunonlar shug'ullangan uzluksiz nisbatlar nazariyasidan olingan.

Bu har bir a'zosi oldingisiga teng bo'lgan, bir xil raqam bilan qo'shilgan sonli ketma-ketlikdir. Bu raqam farq deb ataladi arifmetik progressiya va belgilangan.

Qaysi sonlar ketma-ketligi arifmetik progressiya ekanligini va qaysi biri emasligini aniqlashga harakat qiling:

a)
b)
c)
d)

Tushundim? Javoblarimizni solishtiring:
Bu an arifmetik progressiya - b, c.
Emas arifmetik progressiya - a, d.

Keling, berilgan progressiyaga () qaytaylik va uning th a'zosining qiymatini topishga harakat qilaylik. Mavjud ikki uni topish usuli.

1. Usul

Progressiya sonining oldingi qiymatiga progressiyaning uchinchi hadiga yetguncha qo'shishimiz mumkin. Xulosa qilish uchun ko'p narsa yo'qligi yaxshi - faqat uchta qiymat:

Demak, tasvirlangan arifmetik progressiyaning --chi a'zosi ga teng.

2. Usul

Agar progressiyaning uchinchi hadining qiymatini topish kerak bo'lsa-chi? Xulosa qilish bizni bir soatdan ko'proq vaqt talab qilgan bo'lardi va raqamlarni qo'shishda xato qilmaganimiz haqiqat emas.
Albatta, matematiklar arifmetik progressiyaning farqini oldingi qiymatga qo‘shish shart bo‘lmagan usulni o‘ylab topishdi. Chizilgan rasmga diqqat bilan qarang ... Albatta, siz allaqachon ma'lum bir naqshni payqadingiz, xususan:

Masalan, ushbu arifmetik progressiyaning --chi a'zosining qiymati nimadan iboratligini ko'rib chiqamiz:


Boshqa so'zlar bilan aytganda:

Ushbu arifmetik progressiya a'zosining qiymatini shu tarzda mustaqil ravishda topishga harakat qiling.

Hisoblanganmi? Yozuvlaringizni javob bilan solishtiring:

E'tibor bering, biz oldingi qiymatga arifmetik progressiya a'zolarini ketma-ket qo'shganda oldingi usuldagi kabi raqamni oldingiz.
Keling, ushbu formulani "shaxsiylashtirishga" harakat qilaylik - biz uni umumiy shaklga keltiramiz va olamiz:

Arifmetik progressiya tenglamasi.

Arifmetik progressiyalar ortib boradi yoki kamayadi.

Ortib bormoqda- shartlarning har bir keyingi qiymati oldingisidan katta bo'lgan progressiyalar.
Masalan:

Pastga- shartlarning har bir keyingi qiymati oldingisidan kichik bo'lgan progressiyalar.
Masalan:

Olingan formuladan arifmetik progressiyaning o'suvchi va kamayuvchi hadlaridagi hadlarni hisoblashda foydalaniladi.
Keling, buni amalda tekshirib ko'ramiz.
Bizga quyidagi raqamlardan iborat arifmetik progressiya berilgan:

O'shandan beri:

Shunday qilib, biz formulaning arifmetik progressiyani kamaytirishda ham, oshirishda ham ishlashiga amin bo'ldik.
Ushbu arifmetik progressiyaning --chi va --chi a'zolarini o'zingiz topishga harakat qiling.

Keling, natijalarni taqqoslaylik:

Arifmetik progressiya xossasi

Keling, vazifani murakkablashtiramiz - arifmetik progressiyaning xossasini olamiz.
Aytaylik, bizga quyidagi shart berilgan:
- arifmetik progressiya, qiymatini toping.
Bu oson, deysiz va siz allaqachon bilgan formula bo'yicha hisoblashni boshlaysiz:

Keling, a, keyin:

Mutlaqo to'g'ri. Ma'lum bo'lishicha, biz avval topamiz, keyin uni birinchi raqamga qo'shamiz va biz izlayotgan narsamizni olamiz. Agar progressiya kichik qiymatlar bilan ifodalangan bo'lsa, unda bu erda hech qanday murakkab narsa yo'q, lekin agar bizga shartlarda raqamlar berilsa nima bo'ladi? Qabul qiling, hisob-kitoblarda xato qilish ehtimoli bor.
Endi o'ylab ko'ring, har qanday formula yordamida bu masalani bir bosqichda hal qilish mumkinmi? Albatta, ha, va biz hozir uni chiqarishga harakat qilamiz.

Arifmetik progressiyaning kerakli atamasini quyidagicha belgilaymiz, biz uni topish formulasini bilamiz - bu biz boshida olingan formuladir:
, keyin:

• progressiyaning oldingi a'zosi:
• progressiyaning keyingi muddati:

Progressiyaning oldingi va keyingi a'zolarini jamlaymiz:

Ma’lum bo‘lishicha, progressiyaning oldingi va keyingi a’zolari yig‘indisi ular orasida joylashgan progressiya a’zosining qiymatidan ikki barobarga teng. Boshqacha qilib aytganda, oldingi va ketma-ket qiymatlari ma'lum bo'lgan progressiya a'zosining qiymatini topish uchun ularni qo'shish va bo'lish kerak.

To'g'ri, bizda bir xil raqam bor. Keling, materialni tuzatamiz. Progressiya qiymatini o'zingiz hisoblang, chunki bu umuman qiyin emas.

Juda qoyil! Siz taraqqiyot haqida deyarli hamma narsani bilasiz! Afsonaga ko'ra, barcha davrlarning eng buyuk matematiklaridan biri, "matematiklar qiroli" - Karl Gauss o'zi uchun osonlikcha xulosa qilgan yagona formulani topish qoladi ...

Karl Gauss 9 yoshga to'lganda, o'qituvchi boshqa sinf o'quvchilarining ishini tekshirish bilan mashg'ul bo'lib, darsda quyidagi vazifani qo'ydi: "Barcha natural sonlarning yig'indisini (boshqa manbalarga ko'ra) inklyuzivgacha hisoblang. " Bir daqiqadan so'ng uning shogirdlaridan biri (bu Karl Gauss edi) topshiriqga to'g'ri javob berganida, o'qituvchini ajablantiradigan narsa bo'lsa, jasur sinfdoshlarining ko'pchiligi uzoq hisob-kitoblardan so'ng noto'g'ri natija olishdi ...

Yosh Karl Gauss siz osongina sezishingiz mumkin bo'lgan naqshni payqadi.
Aytaylik, bizda -ti a'zolaridan iborat arifmetik progressiya bor: Arifmetik progressiyaning berilgan a'zolari yig'indisini topishimiz kerak. Albatta, biz barcha qiymatlarni qo'lda yig'ishimiz mumkin, ammo Gauss izlayotganidek, topshiriqda uning shartlari yig'indisini topish kerak bo'lsa-chi?

Keling, bizga berilgan taraqqiyotni tasvirlaylik. Belgilangan raqamlarga diqqat bilan qarang va ular bilan turli matematik operatsiyalarni bajarishga harakat qiling.


Sinab ko'rdingizmi? Nimani sezdingiz? To'g'ri! Ularning miqdori teng

Endi javob bering, bizga berilgan progressiyada shunday juftliklar nechta bo'ladi? Albatta, barcha raqamlarning to'liq yarmi, ya'ni.
Arifmetik progressiyaning ikki a'zosining yig'indisi teng va shunga o'xshash teng juftliklarga asoslanib, biz shuni olamiz umumiy qiymat teng:
.
Shunday qilib, har qanday arifmetik progressiyaning birinchi hadlari yig'indisi formulasi:

Ba'zi masalalarda biz th atamani bilmaymiz, lekin progressiyaning farqini bilamiz. Yig'indi formulasida th a'zosining formulasini qo'yishga harakat qiling.
Nima oldingiz?

Juda qoyil! Endi Karl Gaussga berilgan masalaga qaytaylik: o'zingiz hisoblab ko'ring --dan boshlanadigan sonlar yig'indisi va --dan boshlanadigan sonlar yig'indisi.

Qancha oldingiz?
Gauss hadlar yig'indisi teng, va hadlar yig'indisi ekanligini aniqladi. Siz shunday qaror qildingizmi?

Darhaqiqat, arifmetik progressiya a'zolari yig'indisi formulasini qadimgi yunon olimi Diofant 3-asrda isbotlagan va shu vaqt davomida zukkolar arifmetik progressiyaning xususiyatlaridan kuch va asosiy bilan foydalanganlar.
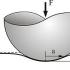
Masalan, tasavvur qiling Qadimgi Misr va o'sha davrdagi eng katta qurilish maydoni - piramida qurilishi ... Rasmda uning bir tomoni ko'rsatilgan.

Bu yerda taraqqiyot qayerda deysiz? Ehtiyotkorlik bilan qarang va piramida devorining har bir qatoridagi qum bloklari sonidagi naqshni toping.


Nega arifmetik progressiya emas? Agar poydevorga blokli g'isht qo'yilgan bo'lsa, bitta devor qurish uchun qancha blok kerakligini hisoblang. Umid qilamanki, barmog'ingizni monitor bo'ylab harakatlantirib hisoblamaysiz, oxirgi formulani va arifmetik progressiya haqida aytgan hamma narsani eslaysizmi?

V bu holat taraqqiyot quyidagicha ko'rinadi:
Arifmetik progressiya farqi.
Arifmetik progressiyaning a'zolari soni.
Keling, ma'lumotlarimizni oxirgi formulalarga almashtiramiz (biz bloklar sonini 2 usulda hisoblaymiz).

1-usul.

2-usul.

Va endi siz monitorda ham hisoblashingiz mumkin: olingan qiymatlarni bizning piramidamizdagi bloklar soni bilan solishtiring. Bu rozi bo'ldimi? Yaxshi, siz arifmetik progressiyaning uchinchi hadlari yig'indisini o'zlashtirib oldingiz.
Albatta, siz poydevordagi bloklardan piramida qura olmaysiz, lekin undanmi? Ushbu shart bilan devor qurish uchun qancha qum g'ishtlari kerakligini hisoblashga harakat qiling.
Siz boshqardingizmi?
To'g'ri javob bloklar:

Ishlab chiqish; mashqa qilish

Vazifalar:

1. Masha yoz uchun formaga tushmoqda. Har kuni u chayqalishlar sonini ko'paytiradi. Agar Masha birinchi mashg'ulotda chayqalsa, haftada necha marta cho'kadi.
2. Tarkibidagi barcha toq raqamlarning yig'indisi nimaga teng.
3. Jurnallarni saqlashda yog'och ishlab chiqaruvchilar ularni shunday qilib yig'adilarki, har bir yuqori qatlam oldingisiga qaraganda bitta kamroq logni o'z ichiga oladi. Agar toshning asosi loglar bo'lsa, bitta devorda qancha log bor.

Javoblar:

1. Arifmetik progressiyaning parametrlarini aniqlaylik. Ushbu holatda
   (hafta = kunlar).

   Javob: Ikki hafta ichida Masha kuniga bir marta chayqalishi kerak.

2. Birinchidan toq raqam, oxirgi raqam.
   Arifmetik progressiya farqi.
   Toq sonlar soni - yarmida, ammo bu faktni arifmetik progressiyaning --chi a'zosini topish formulasi yordamida tekshiring:

   Raqamlar toq raqamlarni o'z ichiga oladi.
   Biz mavjud ma'lumotlarni formulaga almashtiramiz:

   Javob: Tarkibidagi barcha toq sonlar yig'indisi ga teng.

3. Piramidalar haqidagi muammoni eslang. Bizning holatlarimiz uchun a , har bir yuqori qatlam bir jurnalga qisqartirilganligi sababli, faqat bir guruh qatlamlar mavjud, ya'ni.
   Formuladagi ma'lumotlarni almashtiring:

   Javob: Duvarcılıkda loglar mavjud.

Xulosa qilish

1. - qo'shni sonlar orasidagi farq bir xil va teng bo'lgan sonli ketma-ketlik. U ortib bormoqda va kamaymoqda.
2. Formulani topish arifmetik progressiyaning th a'zosi - formula bilan yoziladi, bu erda progressiyadagi sonlar soni.
3. Arifmetik progressiya a'zolarining xossasi- - bu yerda - progressiyadagi sonlar soni.
4. Arifmetik progressiya a'zolari yig'indisi ikki shaklda topish mumkin:
   
   , bu yerda qiymatlar soni.

ARIFMETIK PROGRESSIYA. O'RTACHA DARAJASI

Raqamli ketma-ketlik

Keling, o'tirib, bir nechta raqamlarni yozishni boshlaylik. Masalan:

Siz har qanday raqamlarni yozishingiz mumkin va ular xohlagancha ko'p bo'lishi mumkin. Lekin siz har doim ulardan qaysi biri birinchi, qaysi ikkinchi va hokazo, ya'ni ularni raqamlashimiz mumkin. Bu raqamlar ketma-ketligiga misol.

Raqamli ketma-ketlik raqamlar to'plami bo'lib, ularning har biriga o'ziga xos raqam berilishi mumkin.

Boshqacha qilib aytganda, har bir raqam ma'lum bir natural son bilan bog'lanishi mumkin va faqat bitta. Va biz bu raqamni ushbu to'plamdagi boshqa raqamga tayinlamaymiz.

Raqamli son qatorning --chi a'zosi deyiladi.

Biz odatda butun ketma-ketlikni qandaydir harf deb ataymiz (masalan,), va bu ketma-ketlikning har bir a'zosi - bu a'zoning soniga teng indeksli bir xil harf: .

Ketma-ketlikning --chi a'zosi qandaydir formula bilan berilishi juda qulay. Masalan, formula

ketma-ketlikni belgilaydi:

Va formula quyidagi ketma-ketlikda:

Masalan, arifmetik progressiya ketma-ketlikdir (bu erda birinchi had teng va farq). Yoki (, farq).

n-sonli formula

Biz takroriy formulani chaqiramiz, unda --chi atamani bilish uchun oldingi yoki bir nechta oldingilarini bilishingiz kerak:

Masalan, bunday formuladan foydalanib, progressiyaning uchinchi hadini topish uchun biz oldingi to'qqiztasini hisoblashimiz kerak. Masalan, keling. Keyin:

Xo'sh, endi formula nima ekanligi aniqmi?

Har bir satrda biz qo'shamiz, ba'zi bir raqamga ko'paytiramiz. Nima uchun? Juda oddiy: bu joriy a'zoning soni minus:

Hozir ancha qulayroq, to'g'rimi? Biz tekshiramiz:

O'zingiz qaror qiling:

Arifmetik progressiyada n-hashning formulasini toping va yuzinchi hadni toping.

Yechim:

Birinchi a'zo teng. Va qanday farq bor? Va mana nima:

(Axir u progressiyaning ketma-ket a'zolari ayirmasiga teng bo'lgani uchun farq deyiladi).

Shunday qilib, formula:

Keyin yuzinchi had:

dan gacha bo'lgan barcha natural sonlarning yig'indisi nechaga teng?

Afsonaga ko'ra, buyuk matematik Karl Gauss 9 yoshli bolaligida bu miqdorni bir necha daqiqada hisoblab chiqdi. U birinchi va oxirgi sonning yig'indisi teng ekanligini, ikkinchi va oxirgi sonning yig'indisi bir xil ekanligini, oxiridan uchinchi va uchinchi sonning yig'indisi bir xil ekanligini va hokazo. Bunday juftliklar nechta? To'g'ri, barcha raqamlarning yarmi soni, ya'ni. Shunday qilib,

Har qanday arifmetik progressiyaning birinchi hadlari yig‘indisining umumiy formulasi quyidagicha bo‘ladi:

Misol:
Barcha ikki xonali karralilarning yig‘indisini toping.

Yechim:

Birinchi bunday raqam bu. Har bir keyingi raqam oldingisiga raqam qo'shish orqali olinadi. Shunday qilib, bizni qiziqtirgan raqamlar birinchi had va farq bilan arifmetik progressiya hosil qiladi.

Ushbu progressiyaning uchinchi hadi formulasi:

Progressiyada nechta had bor, agar ularning hammasi ikki xonali bo‘lishi kerak?

Juda oson: .

Progressiyaning oxirgi muddati teng bo'ladi. Keyin summa:

Javob: .

Endi o'zingiz qaror qiling:

1. Har kuni sportchi oldingi kunga qaraganda 1 m ko'proq yuguradi. Agar birinchi kuni km m ga yugursa, u haftada necha kilometr yuguradi?
2. Velosipedchi har kuni oldingisiga qaraganda ko'proq mil yuradi. Birinchi kuni u km yo'l bosib o'tdi. Bir kilometrni bosib o‘tish uchun u necha kun yurishi kerak? Sayohatning oxirgi kunida u necha kilometr yuradi?
3. Do'kondagi muzlatgichning narxi har yili bir xil miqdorda kamayadi. Agar sotuvga rublga qo'yilgan bo'lsa, olti yildan so'ng u rublga sotilgan bo'lsa, muzlatgich narxi har yili qanchaga tushganini aniqlang.

Javoblar:

1. Bu erda eng muhimi arifmetik progressiyani tanib olish va uning parametrlarini aniqlashdir. Bunday holda, (hafta = kunlar). Ushbu progressiyaning birinchi shartlari yig'indisini aniqlashingiz kerak:
   .
   Javob:
2. Bu erda berilgan:, topish kerak.
   Shubhasiz, oldingi muammodagi kabi bir xil yig'indi formulasidan foydalanishingiz kerak:
   .
   Qiymatlarni almashtiring:

   Ildiz aniq mos kelmaydi, shuning uchun javob.
   Oxirgi kun davomida bosib o‘tgan yo‘lni -chi had formulasi yordamida hisoblaymiz:
   (km).
   Javob:

3. Berilgan: . Toping: .
   Bu osonlashmaydi:
   (rub).
   Javob:

ARIFMETIK PROGRESSIYA. ASOSIY HAQIDA QISQA

Bu qo'shni raqamlar orasidagi farq bir xil va teng bo'lgan sonli ketma-ketlikdir.

Arifmetik progressiya ortib bormoqda () va kamaymoqda ().

Masalan:

Arifmetik progressiyaning n-azosini topish formulasi

formula sifatida yoziladi, bu erda progressiyadagi sonlar soni.

Arifmetik progressiya a'zolarining xossasi

Bu progressiyaning a'zosini topishni osonlashtiradi, agar uning qo'shni a'zolari ma'lum bo'lsa - progressiyadagi sonlar soni qayerda.

Arifmetik progressiya a'zolari yig'indisi

Yig'indini topishning ikki yo'li mavjud:

Qaerda qiymatlar soni.

Qaerda qiymatlar soni.

Ha, ha: arifmetik progressiya siz uchun o'yinchoq emas :)

Xo'sh, do'stlar, agar siz ushbu matnni o'qiyotgan bo'lsangiz, unda ichki qopqoq dalillari menga arifmetik progressiya nima ekanligini hali ham bilmasligingizni aytadi, lekin siz haqiqatan ham (yo'q, shunday: SOOOOO!) bilishni xohlaysiz. Shuning uchun, men sizni uzoq tanishuvlar bilan qiynamayman va darhol ish bilan shug'ullanaman.

Boshlash uchun bir nechta misol. Bir nechta raqamlar to'plamini ko'rib chiqing:

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $\sqrt(2);\ 2\sqrt(2);\ 3\sqrt(2);...$

Ushbu to'plamlarning barchasida qanday umumiylik bor? Bir qarashda, hech narsa. Lekin aslida nimadir bor. Aynan: har bir keyingi element avvalgisidan bir xil raqam bilan farq qiladi.

O'zingiz uchun hukm qiling. Birinchi to'plam faqat ketma-ket raqamlar bo'lib, ularning har biri avvalgisidan ko'proq. Ikkinchi holda, qo'shni raqamlar orasidagi farq allaqachon beshga teng, ammo bu farq hali ham doimiy. Uchinchi holatda, umuman olganda, ildizlar mavjud. Biroq, $2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, ya'ni. bu holda har bir keyingi element oddiygina $\sqrt(2)$ ga ortadi (va bu raqam mantiqiy emasligidan qo'rqmang).

Shunday qilib: barcha bunday ketma-ketliklar faqat arifmetik progressiyalar deb ataladi. Keling, qat'iy ta'rif beraylik:

Ta'rif. Har bir keyingisi oldingisidan aynan bir xil miqdorda farq qiladigan raqamlar ketma-ketligiga arifmetik progressiya deyiladi. Raqamlar bir-biridan farq qiladigan miqdor progressiya farqi deb ataladi va ko'pincha $d$ harfi bilan belgilanadi.

Belgilanish: $\left(((a)_(n)) \right)$ - progressiyaning o'zi, $d$ - uning farqi.

Va faqat bir nechta muhim izohlar. Birinchidan, faqat rivojlanish hisobga olinadi tartibli raqamlar ketma-ketligi: ularni yozilish tartibida qat'iy ravishda o'qishga ruxsat beriladi - va boshqa hech narsa. Siz raqamlarni o'zgartira olmaysiz yoki almashtira olmaysiz.

Ikkinchidan, ketma-ketlikning o'zi chekli yoki cheksiz bo'lishi mumkin. Masalan, (1; 2; 3) to'plam aniq arifmetik progressiyadir. Ammo agar siz (1; 2; 3; 4; ...) kabi biror narsa yozsangiz - bu allaqachon cheksiz progressiyadir. To'rtdan keyin ellips, go'yo, juda ko'p raqamlar oldinga borishini ko'rsatadi. Masalan, cheksiz ko'p. :)

Shuni ham ta'kidlashni istardimki, progressiyalar ortib bormoqda va kamaymoqda. Biz allaqachon ortib borayotganlarni ko'rdik - bir xil to'plam (1; 2; 3; 4; ...). Bu erda progressiyaning pasayishiga misollar:

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $\sqrt(5);\ \sqrt(5)-1;\ \sqrt(5)-2;\ \sqrt(5)-3;...$

Mayli mayli: oxirgi misol haddan tashqari murakkab tuyulishi mumkin. Ammo qolganlari, menimcha, tushunasiz. Shuning uchun biz yangi ta'riflarni kiritamiz:

Ta'rif. Arifmetik progressiya deyiladi:

1. har bir keyingi element avvalgisidan kattaroq bo'lsa, ortib boradi;
2. kamaytirish, agar, aksincha, har bir keyingi element avvalgisidan kamroq bo'lsa.

Bundan tashqari, "statsionar" ketma-ketliklar mavjud - ular bir xil takrorlanuvchi raqamdan iborat. Masalan, (3; 3; 3; ...).

Faqat bitta savol qoladi: ortib borayotgan progressiyani pasayishdan qanday ajratish mumkin? Yaxshiyamki, bu erda hamma narsa faqat $ d$ raqamining belgisiga bog'liq, ya'ni. Progressiv farqlar:

1. Agar $d \gt 0$ bo'lsa, u holda progressiya ortib bormoqda;
2. Agar $d \lt 0$ bo'lsa, unda progressiya aniq pasaymoqda;
3. Va nihoyat, $d=0$ holati bor - bu holda butun progressiya bir xil sonlarning statsionar ketma-ketligiga tushiriladi: (1; 1; 1; 1; ...) va hokazo.

Yuqoridagi uchta kamayuvchi progressiya uchun $d$ farqini hisoblashga harakat qilaylik. Buning uchun har qanday ikkita qo'shni elementni (masalan, birinchi va ikkinchi) olish va o'ngdagi raqamdan, chapdagi raqamni ayirish kifoya. Bu shunday ko'rinadi:

• 41−49=−8;
• 12−17,5=−5,5;
• $\sqrt(5)-1-\sqrt(5)=-1$.

Ko'rib turganingizdek, har uch holatda ham farq haqiqatan ham salbiy bo'lib chiqdi. Va endi biz ko'proq yoki kamroq ta'riflarni aniqladik, progressiyalar qanday tasvirlanganligini va ular qanday xususiyatlarga ega ekanligini aniqlash vaqti keldi.

Progressiya a'zolari va takroriy formula

Bizning ketma-ketliklarimizning elementlarini almashtirib bo'lmagani uchun ularni raqamlash mumkin:

\[\left(((a)_(n)) \o'ng)=\left\(((a)_(1)),\ ((a)_(2)),((a)_(3) )),... \o'ng\)\]

Bu to'plamning alohida elementlari progressiya a'zolari deb ataladi. Ular son yordamida shunday ko'rsatiladi: birinchi a'zo, ikkinchi a'zo va hokazo.

Bundan tashqari, biz allaqachon bilganimizdek, progressiyaning qo'shni a'zolari quyidagi formula bo'yicha bog'langan:

\[((a)_(n))-((a)_(n-1))=d\O'ng strelka ((a)_(n))=((a)_(n-1))+d \]

Xulosa qilib aytganda, progressiyaning $n$-chi hadini topish uchun siz $n-1$-chi had va $d$ farqini bilishingiz kerak. Bunday formula takroriy deb ataladi, chunki uning yordami bilan har qanday raqamni topishingiz mumkin, faqat oldingisini (va aslida barcha oldingilarni) bilib olasiz. Bu juda noqulay, shuning uchun har qanday hisobni birinchi atama va farqga qisqartiradigan yanada murakkab formula mavjud:

\[((a)_(n))=((a)_(1))+\chap(n-1 \o'ng)d\]

Ehtimol, siz bu formulaga avvalroq duch kelgansiz. Ular buni har xil ma'lumotnomalar va reshebniklarda berishni yaxshi ko'radilar. Va matematika bo'yicha har qanday oqilona darslikda u birinchilardan biridir.

Biroq, men sizga ozgina mashq qilishni maslahat beraman.

Vazifa raqami 1. $((a)_(1))=8,d=-5$ bo'lsa, $\left(((a)_(n)) \right)$ arifmetik progressiyaning dastlabki uchta hadini yozing.

Yechim. Demak, biz $((a)_(1))=8$ birinchi hadini va $d=-5$ progressiya farqini bilamiz. Keling, berilgan formuladan foydalanib, $n=1$, $n=2$ va $n=3$ oʻrniga qoʻyaylik:

\[\begin(align) & (a)_(n))=((a)_(1))+\left(n-1 \right)d; \\ & ((a)_(1))=((a)_(1))+\left(1-1 \right)d=((a)_(1))=8; \\ & ((a)_(2))=((a)_(1))+\chap(2-1 \o'ng)d=((a)_(1))+d=8-5= 3; \\ & ((a)_(3))=((a)_(1))+\chap(3-1 \o'ng)d=((a)_(1))+2d=8-10= -2. \\ \end (tekislash)\]

Javob: (8; 3; -2)

Ana xolos! E'tibor bering, bizning taraqqiyotimiz pasayib bormoqda.

Albatta, $n=1$ oʻrnini bosish mumkin emas edi – biz birinchi atamani allaqachon bilamiz. Biroq, birlikni almashtirish orqali biz formulamiz birinchi muddatda ham ishlashiga ishonch hosil qildik. Boshqa hollarda, hamma narsa banal arifmetikaga tushdi.

Vazifa raqami 2. Arifmetik progressiyaning yettinchi hadi −40 va o‘n yettinchi hadi −50 bo‘lsa, uning dastlabki uchta hadini yozing.

Yechim. Muammoning shartini odatdagidek yozamiz:

\[((a)_(7))=-40;\quad ((a)_(17))=-50.\]

\[\left\( \begin(align) & ((a)_(7))=((a)_(1))+6d \\ & (a)_(17))=((a) _(1))+16d \\ \end(tekislash) \o'ngga.\]

\[\left\( \begin(align) & ((a)_(1))+6d=-40 \\ & (a)_(1))+16d=-50 \\ \end(hizala) \o'ng.\]

Men tizimning belgisini qo'ydim, chunki bu talablar bir vaqtning o'zida bajarilishi kerak. Va endi shuni ta'kidlaymizki, agar biz ikkinchi tenglamadan birinchi tenglamani ayirsak (biz buni qilishga haqlimiz, chunki bizda tizim mavjud), biz buni olamiz:

\[\begin(align) & ((a)_(1))+16d-\left(((a)_(1))+6d \right)=-50-\left(-40 \right); \\ & ((a)_(1))+16d-((a)_(1))-6d=-50+40; \\ & 10d=-10; \\&d=-1. \\ \end (tekislash)\]

Xuddi shunday, biz progressiv farqni topdik! Tizimning istalgan tenglamalarida topilgan raqamni almashtirish qoladi. Masalan, birinchisida:

\[\begin(matritsa) ((a)_(1))+6d=-40;\quad d=-1 \\ \Downrow \\ ((a)_(1))-6=-40; \\ ((a)_(1))=-40+6=-34. \\ \end (matritsa)\]

Endi birinchi atama va farqni bilib, ikkinchi va uchinchi shartlarni topish qoladi:

\[\begin(align) & ((a)_(2))=((a)_(1))+d=-34-1=-35; \\ & ((a)_(3))=((a)_(1))+2d=-34-2=-36. \\ \end (tekislash)\]

Tayyor! Muammo hal qilindi.

Javob: (-34; -35; -36)

Biz kashf etgan progressiyaning qiziq bir xususiyatiga e'tibor bering: agar biz $n$th va $m$th shartlarini olib, ularni bir-biridan ayirish bilan, progressiyaning farqini $n-m$ soniga ko'paytiramiz:

\[((a)_(n))-((a)_(m))=d\cdot \left(n-m \o'ng)\]

Oddiy, lekin juda foydali mulk, albatta, siz bilishingiz kerak - uning yordami bilan progressivlikdagi ko'plab muammolarni hal qilishni sezilarli darajada tezlashtirishingiz mumkin. Mana buning asosiy misoli:

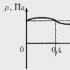
Vazifa raqami 3. Arifmetik progressiyaning beshinchi hadi 8,4 ga, o‘ninchi hadi esa 14,4 ga teng. Bu progressiyaning o‘n beshinchi hadini toping.

Yechim. $((a)_(5))=8.4$, $((a)_(10))=14.4$ boʻlgani uchun va biz $((a)_(15))$ topishimiz kerak boʻlgani uchun biz quyidagilarni qayd qilamiz:

\[\begin(align) & ((a)_(15))-((a)_(10))=5d; \\ & ((a)_(10))-((a)_(5))=5d. \\ \end (tekislash)\]

Lekin $((a)_(10))-((a)_(5))=14.4-8.4=6$ sharti boʻyicha $5d=6$, bizda:

\[\begin(align) & ((a)_(15))-14,4=6; \\ & ((a)_(15))=6+14,4=20,4. \\ \end (tekislash)\]

Javob: 20.4

Ana xolos! Bizga hech qanday tenglamalar tizimini tuzish va birinchi had va farqni hisoblash kerak emas edi - hamma narsa bir-ikki qatorda hal qilindi.

Keling, muammoning yana bir turini ko'rib chiqaylik - progressiyaning salbiy va ijobiy a'zolarini izlash. Hech kimga sir emaski, agar progressiya oshib borsa, uning birinchi muddati salbiy bo'lsa, unda ertami-kechmi ijobiy atamalar paydo bo'ladi. Va aksincha: kamayib borayotgan progressiyaning shartlari ertami-kechmi salbiy bo'ladi.

Shu bilan birga, elementlarni ketma-ket saralab, ushbu daqiqani "peshonada" topish har doim ham mumkin emas. Ko'pincha, muammolar formulalarni bilmasdan turib, hisob-kitoblar bir nechta varaqlarni oladi - javob topgunimizcha uxlab qolamiz. Shuning uchun biz bu muammolarni tezroq hal qilishga harakat qilamiz.

Vazifa raqami 4. Arifmetik progressiyada nechta manfiy had -38,5; -35,8; …?

Yechim. Shunday qilib, $((a)_(1))=-38,5$, $((a)_(2))=-35,8$, shundan biz darhol farqni topamiz:

E'tibor bering, farq ijobiydir, shuning uchun rivojlanish ortib bormoqda. Birinchi atama manfiy, shuning uchun haqiqatan ham bir nuqtada biz ijobiy raqamlarga qoqilib qolamiz. Bitta savol - bu qachon sodir bo'ladi.

Keling, bilishga harakat qilaylik: qancha vaqtgacha (ya'ni, nimagacha natural son$n$) atamalarning salbiyligi saqlanib qoladi:

\[\begin(align) & ((a)_(n)) \lt 0\O'ng strelka ((a)_(1))+\left(n-1 \o'ng)d \lt 0; \\ & -38,5+\left(n-1 \o'ng)\cdot 2,7 \lt 0;\quad \left| \cdot 10 \o'ng. \\ & -385+27\cdot \left(n-1 \o'ng) \lt 0; \\ & -385+27n-27 \lt 0; \\ & 27n \lt 412; \\ & n \lt 15\frac(7)(27)\O'ng strelka ((n)_(\max ))=15. \\ \end (tekislash)\]

Oxirgi qatorga tushuntirish kerak. Shunday qilib, biz $n \lt 15\frac(7)(27)$ ekanligini bilamiz. Boshqa tomondan, bizga raqamning faqat butun qiymatlari mos keladi (bundan tashqari: $n\in \mathbb(N)$), shuning uchun ruxsat etilgan eng katta raqam aniq $n=15$ va hech qanday holatda 16 emas.

Vazifa raqami 5. Arifmetik progressiyada $(()_(5))=-150,(()_(6))=-147$. Bu progressiyaning birinchi musbat hadining sonini toping.

Bu avvalgisi bilan bir xil muammo bo'ladi, lekin biz $((a)_(1))$ ni bilmaymiz. Ammo qo'shni shartlar ma'lum: $((a)_(5))$ va $((a)_(6))$, shuning uchun biz progressiya farqini osongina topishimiz mumkin:

Bundan tashqari, standart formuladan foydalanib, beshinchi atamani birinchi va farq jihatidan ifodalashga harakat qilaylik:

\[\begin(align) & ((a)_(n))=((a)_(1))+\left(n-1 \right)\cdot d; \\ & ((a)_(5))=((a)_(1))+4d; \\ & -150=((a)_(1))+4\cdot 3; \\ & ((a)_(1))=-150-12=-162. \\ \end (tekislash)\]

Endi biz oldingi muammoga o'xshashlik bilan davom etamiz. Ijobiy raqamlar ketma-ketligimizning qaysi nuqtasida paydo bo'lishini bilib olamiz:

\[\begin(align) & ((a)_(n))=-162+\left(n-1 \right)\cdot 3 \gt 0; \\ & -162+3n-3 \gt 0; \\ & 3n \gt 165; \\ & n \gt 55\O'ng strelka ((n)_(\min ))=56. \\ \end (tekislash)\]

Bu tengsizlikning minimal butun yechimi 56 raqamidir.

E'tibor bering, oxirgi vazifada hamma narsa qat'iy tengsizlikka tushirildi, shuning uchun $n=55$ varianti bizga mos kelmaydi.

Oddiy masalalarni yechishni o‘rganganimizdan so‘ng, endi murakkabroq masalalarga o‘tamiz. Ammo birinchi navbatda, arifmetik progressiyaning yana bir foydali xususiyatini bilib olaylik, bu bizga kelajakda ko'p vaqt va teng bo'lmagan hujayralarni tejaydi. :)

O'rtacha arifmetik va teng chegaralar

$\left(((a)_(n)) \right)$ ortib boruvchi arifmetik progressiyaning bir necha ketma-ket shartlarini ko'rib chiqing. Keling, ularni raqamlar qatorida belgilashga harakat qilaylik:

Son qatoridagi arifmetik progressiya a'zolari

Men har qanday $((a)_(1)) emas, balki $((a)_(n-3)),...,((a)_(n+3))$ ixtiyoriy a'zolarini alohida qayd etdim. \ ((a)_(2)),\ ((a)_(3))$ va boshqalar. Chunki men hozir aytib o'tadigan qoida har qanday "segmentlar" uchun bir xil ishlaydi.

Va qoida juda oddiy. Keling, rekursiv formulani eslaylik va uni barcha belgilangan a'zolar uchun yozamiz:

\[\begin(align) & ((a)_(n-2))=((a)_(n-3))+d; \\ & ((a)_(n-1))=((a)_(n-2))+d; \\ & ((a)_(n))=((a)_(n-1))+d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n+1))+d; \\ \end (tekislash)\]

Biroq, bu tengliklarni boshqacha tarzda qayta yozish mumkin:

\[\begin(align) & (a)_(n-1))=((a)_(n))-d; \\ & ((a)_(n-2))=((a)_(n))-2d; \\ & ((a)_(n-3))=((a)_(n))-3d; \\ & ((a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(n+3))=((a)_(n))+3d; \\ \end (tekislash)\]

Xo'sh, nima? Lekin $((a)_(n-1))$ va $((a)_(n+1))$ atamalari $((a)_(n)) $ dan bir xil masofada joylashganligi fakti. . Va bu masofa $d$ ga teng. $((a)_(n-2))$ va $((a)_(n+2))$ atamalari haqida ham shunday deyish mumkin - ular $((a)_(n) dan ham olib tashlangan. )$ bir xil masofada $2d$ ga teng. Siz cheksiz davom etishingiz mumkin, ammo rasm ma'noni yaxshi ko'rsatib beradi

Progressiya a'zolari markazdan bir xil masofada yotadi

Bu biz uchun nimani anglatadi? Bu shuni anglatadiki, agar qo'shni raqamlar ma'lum bo'lsa, $((a)_(n))$ topishingiz mumkin:

\[((a)_(n))=\frac(((a)_(n-1))+((a)_(n+1)))(2)\]

Biz ajoyib xulosa chiqardik: arifmetik progressiyaning har bir a'zosi qo'shni a'zolarning o'rtacha arifmetik qiymatiga teng! Bundan tashqari, biz $((a)_(n))$ dan chapga va o'ngga bir qadam emas, balki $k$ qadamlari bilan og'ishimiz mumkin - va baribir formula to'g'ri bo'ladi:

\[((a)_(n))=\frac(((a)_(n-k))+((a)_(n+k)))(2)\]

Bular. $((a)_(150))$ va $((a)_(100))$ va $((a)_(200))$ ni bilsak, biz osongina $((a)_(150))$ topa olamiz, chunki $(( a)_ (150))=\frac(((a)_(100))+((a)_(200)(2)$. Bir qarashda, bu fakt bizga hech qanday foydali narsa bermayotgandek tuyulishi mumkin. Biroq, amalda ko'plab vazifalar arifmetik o'rtachadan foydalanish uchun maxsus "o'tkirlashadi". Qarab qo'ymoq:

Vazifa raqami 6. $-6((x)^(2))$, $x+1$ va $14+4((x)^(2))$ raqamlari ketma-ket aʼzolari boʻlishi uchun $x$ ning barcha qiymatlarini toping. arifmetik progressiya (belgilangan tartibda).

Yechim. Bu raqamlar progressiyaning a'zolari bo'lgani uchun ular uchun o'rtacha arifmetik shart bajariladi: markaziy element $x+1$ qo'shni elementlar bilan ifodalanishi mumkin:

\[\begin(align) & x+1=\frac(-6((x)^(2))+14+4((x)^(2)))(2); \\ & x+1=\frac(14-2((x)^(2)(2); \\ & x+1=7-((x)^(2)); \\ & ((x)^(2))+x-6=0. \\ \end (tekislash)\]

Bu klassik bo'lib chiqdi kvadrat tenglama. Uning ildizlari: $x=2$ va $x=-3$ javoblardir.

Javob: -3; 2.

Vazifa raqami 7. $-1;4-3;(()^(2))+1$ raqamlari arifmetik progressiya hosil qiladigan (shu tartibda) $$ qiymatlarini toping.

Yechim. Yana oʻrta atamani qoʻshni atamalarning oʻrtacha arifmetik qiymatida ifodalaymiz:

\[\begin(align) & 4x-3=\frac(x-1+((x)^(2))+1)(2); \\ & 4x-3=\frac(((x)^(2))+x)(2);\quad \left| \cdot 2\o'ng.; \\ & 8x-6=((x)^(2))+x; \\ & ((x)^(2))-7x+6=0. \\ \end (tekislash)\]

Yana bir kvadrat tenglama. Va yana ikkita ildiz: $x=6$ va $x=1$.

Javob: 1; 6.

Agar muammoni hal qilish jarayonida siz shafqatsiz raqamlarni olsangiz yoki topilgan javoblarning to'g'riligiga to'liq ishonchingiz komil bo'lmasa, unda tekshirishga imkon beruvchi ajoyib hiyla bor: biz muammoni to'g'ri hal qildikmi?

Aytaylik, 6-masalada biz -3 va 2 javoblarni oldik. Bu javoblarning to'g'riligini qanday tekshirish mumkin? Keling, ularni asl holatga ulab, nima bo'lishini ko'raylik. Sizga shuni eslatib o'tamanki, bizda uchta raqam ($-6(()^(2))$, $+1$ va $14+4(()^(2))$ mavjud bo'lib, ular arifmetik progressiya hosil qilishi kerak. $x=-3$ oʻrniga:

\[\begin(align) & x=-3\Rightarrow \\ & -6((x)^(2))=-54; \\ &x+1=-2; \\ & 14+4((x)^(2))=50. \end(tuzalash)\]

Biz raqamlarni oldik -54; −2; 52 ga farq qiladigan 50, shubhasiz, arifmetik progressiyadir. Xuddi shu narsa $x=2$ uchun sodir bo'ladi:

\[\begin(align) & x=2\Rightarrow \\ & -6((x)^(2))=-24; \\ &x+1=3; \\ & 14+4((x)^(2))=30. \end(tuzalash)\]

Yana progressiya, lekin 27 farq bilan. Shunday qilib, muammo to'g'ri hal qilinadi. Xohlaganlar ikkinchi vazifani mustaqil ravishda tekshirishlari mumkin, lekin men darhol aytaman: u erda ham hamma narsa to'g'ri.

Umuman olganda, oxirgi vazifalarni hal qilishda biz boshqasiga qoqilib qoldik qiziq fakt, buni ham eslash kerak:

Agar uchta raqam shunday bo'lsa, ikkinchisi birinchi va oxirgining o'rtachasi bo'lsa, bu raqamlar arifmetik progressiya hosil qiladi.

Kelajakda ushbu bayonotni tushunish bizga muammoning holatiga qarab kerakli progressiyani tom ma'noda "qurish" imkonini beradi. Ammo bunday "qurilish" bilan shug'ullanishdan oldin, biz allaqachon ko'rib chiqilgan narsadan bevosita kelib chiqadigan yana bir haqiqatga e'tibor qaratishimiz kerak.

Guruhlash va elementlar yig'indisi

Keling, yana raqamlar qatoriga qaytaylik. Biz progressiyaning bir nechta a'zolarini qayd etamiz, ular orasida, ehtimol. boshqa ko'plab a'zolarga arziydi:

Raqamlar qatorida belgilangan 6 ta element

Keling, “chap dum”ni $((a)_(n))$ va $d$, “o‘ng dum”ni esa $((a)_(k))$ va $ shaklida ifodalashga harakat qilaylik. d$. Bu juda oddiy:

\[\begin(align) & (a)_(n+1))=((a)_(n))+d; \\ & ((a)_(n+2))=((a)_(n))+2d; \\ & ((a)_(k-1))=((a)_(k))-d; \\ & ((a)_(k-2))=((a)_(k))-2d. \\ \end (tekislash)\]

Endi e'tibor bering, quyidagi summalar teng:

\[\begin(align) & ((a)_(n))+((a)_(k))=S; \\ & ((a)_(n+1))+((a)_(k-1))=((a)_(n))+d+((a)_(k))-d= S; \\ & ((a)_(n+2))+((a)_(k-2))=((a)_(n))+2d+((a)_(k))-2d= S. \end(tuzalash)\]

Oddiy qilib aytganda, agar biz jami $S$ soniga teng bo'lgan progressiyaning ikkita elementini boshlang'ich deb hisoblasak va keyin biz bu elementlardan qarama-qarshi yo'nalishda (bir-biriga qarab yoki aksincha) qadam tashlashni boshlasak, keyin biz qoqiladigan elementlarning yig'indisi ham teng bo'ladi$S$. Buni eng yaxshi grafik tarzda ifodalash mumkin:

Xuddi shu chegaralar teng miqdorni beradi

Tushunish bu fakt yuqorida ko'rib chiqqanimizdan ko'ra murakkablik darajasi yuqori bo'lgan muammolarni hal qilishga imkon beradi. Masalan, bular:

Vazifa raqami 8. Birinchi hadi 66, ikkinchi va o‘n ikkinchi hadlarning ko‘paytmasi esa mumkin bo‘lgan eng kichik bo‘lgan arifmetik progressiyaning ayirmasini aniqlang.

Yechim. Keling, biz bilgan hamma narsani yozamiz:

\[\begin(align) & ((a)_(1))=66; \\&d=? \\ & ((a)_(2))\cdot ((a)_(12))=\min. \end(tuzalash)\]

Demak, biz $d$ progressiyasining farqini bilmaymiz. Aslida, butun yechim farq atrofida quriladi, chunki $((a)_(2))\cdot ((a)_(12))$ mahsulotini quyidagicha qayta yozish mumkin:

\[\begin(align) & (a)_(2))=((a)_(1))+d=66+d; \\ & ((a)_(12))=((a)_(1))+11d=66+11d; \\ & ((a)_(2))\cdot ((a)_(12))=\left(66+d \o'ng)\cdot \left(66+11d \o'ng)= \\ & =11 \cdot \left(d+66 \o'ng)\cdot \left(d+6 \o'ng). \end(tuzalash)\]

Tankdagilar uchun: men ikkinchi qavsdan umumiy koeffitsient 11 ni oldim. Shunday qilib, kerakli mahsulot $d$ o'zgaruvchisiga nisbatan kvadratik funktsiyadir. Shuning uchun $f\left(d \right)=11\left(d+66 \right)\left(d+6 \right)$ funksiyasini ko‘rib chiqamiz - uning grafigi shoxlari yuqoriga ko‘tarilgan parabola bo‘ladi, chunki Qavslarni ochsak, biz quyidagilarni olamiz:

\[\begin(align) & f\left(d \right)=11\left(((d)^(2))+66d+6d+66\cdot 6 \o'ng)= \\ & =11(( d)^(2))+11\cdot 72d+11\cdot 66\cdot 6 \end(align)\]

Ko'rib turganingizdek, eng yuqori atama koeffitsienti 11 ga teng - bu ijobiy raqam, shuning uchun biz haqiqatan ham shoxlari yuqori bo'lgan parabola bilan ishlaymiz:

jadval kvadratik funktsiya- parabola

Iltimos, diqqat qiling: bu parabola o'zining minimal qiymatini $((d)_(0))$ abscissa bilan o'zining cho'qqisida oladi. Albatta, biz bu abscissani standart sxema bo'yicha hisoblashimiz mumkin ($((d)_(0))=(-b)/(2a)\;$ formulasi mavjud), ammo buni qilish ancha oqilona bo'lar edi. E'tibor bering, kerakli cho'qqi parabolaning o'qi simmetriyasida yotadi, shuning uchun $((d)_(0))$ nuqta $f\left(d \right)=0$ tenglamaning ildizlaridan teng masofada joylashgan:

\[\begin(align) & f\left(d\right)=0; \\ & 11\cdot \left(d+66 \o'ng)\cdot \left(d+6 \o'ng)=0; \\ & ((d)_(1))=-66;\to'rtlik ((d)_(2))=-6. \\ \end (tekislash)\]

Shuning uchun men qavslarni ochishga shoshilmadim: asl shaklda ildizlarni topish juda va juda oson edi. Shuning uchun abscissa −66 va −6 sonlarning oʻrtacha arifmetik qiymatiga teng:

\[((d)_(0))=\frac(-66-6)(2)=-36\]

Bizga topilgan raqamni nima beradi? U bilan kerakli mahsulot eng kichik qiymatni oladi (Aytgancha, biz $((y)_(\min ))$ hisoblamadik - bu bizdan talab qilinmaydi). Shu bilan birga, bu raqam dastlabki progressiyaning farqidir, ya'ni. biz javob topdik. :)

Javob: -36

Vazifa raqami 9. $-\frac(1)(2)$ va $-\frac(1)(6)$ raqamlari orasiga uchta raqamni kiriting, shunda ular berilgan raqamlar bilan birgalikda arifmetik progressiya hosil qiladi.

Yechim. Aslida, birinchi va oxirgi raqam allaqachon ma'lum bo'lgan beshta raqamdan iborat ketma-ketlikni yaratishimiz kerak. Yetishmayotgan raqamlarni $x$, $y$ va $z$ oʻzgaruvchilari bilan belgilang:

\[\left(((a)_(n)) \o'ng)=\left\( -\frac(1)(2);x;y;z;-\frac(1)(6) \o'ng\ )\]

E'tibor bering, $y$ raqami ketma-ketligimizning "o'rtasi" - u $x$ va $z$ raqamlaridan, $-\frac(1)(2)$ va $-\frac raqamlaridan bir xil masofada joylashgan. (1)(6)$. Va agar $x$ va $z$ raqamlaridan biz bo'lsak bu daqiqa biz $y $ ni ololmaymiz, keyin progressiyaning uchlari bilan vaziyat boshqacha. O'rtacha arifmetikni eslang:

Endi $y$-ni bilib, qolgan raqamlarni topamiz. E'tibor bering, $x$ $-\frac(1)(2)$ va $y=-\frac(1)(3)$ orasida joylashgan. Shunday qilib

Xuddi shunday bahslashib, qolgan raqamni topamiz:

Tayyor! Biz uchta raqamni topdik. Keling, ularni javobda asl raqamlar orasiga qo'yish kerak bo'lgan tartibda yozamiz.

Javob: $-\frac(5)(12);\ -\frac(1)(3);\ -\frac(1)(4)$

Vazifa raqami 10. 2 va 42 raqamlari orasiga, agar kiritilgan sonlarning birinchi, ikkinchi va oxirgisi yigʻindisi 56 ga teng ekanligi maʼlum boʻlsa, berilgan sonlar bilan birgalikda arifmetik progressiya hosil qiluvchi bir nechta raqamlarni qoʻying.

Yechim. Bundan ham qiyinroq vazifa, ammo avvalgilari kabi hal qilinadi - o'rtacha arifmetik orqali. Muammo shundaki, biz qancha raqam kiritishni aniq bilmaymiz. Shuning uchun, aniqlik uchun biz kiritgandan so'ng aniq $n$ raqamlari bo'ladi deb faraz qilamiz va ularning birinchisi 2, oxirgisi esa 42. Bu holda kerakli arifmetik progressiyani quyidagicha ifodalash mumkin:

\[\left(((a)_(n)) \right)=\left\( 2;((a)_(2));((a)_(3));...;(( a)_(n-1));42 \o'ng\)\]

\[((a)_(2))+((a)_(3))+((a)_(n-1))=56\]

Biroq, $((a)_(2))$ va $((a)_(n-1))$ raqamlari bir-biriga qarab bir qadam chetida turgan 2 va 42 raqamlaridan olinganligini unutmang. , ya'ni. ketma-ketlikning markaziga. Va bu shuni anglatadiki

\[((a)_(2))+((a)_(n-1))=2+42=44\]

Ammo keyin yuqoridagi iborani shunday qayta yozish mumkin:

\[\begin(align) & ((a)_(2))+((a)_(3))+((a)_(n-1))=56; \\ & \left(((a)_(2))+((a)_(n-1)) \right)+((a)_(3))=56; \\ & 44+((a)_(3))=56; \\ & ((a)_(3))=56-44=12. \\ \end (tekislash)\]

$((a)_(3))$ va $((a)_(1))$ bilgan holda biz progressiya farqini osongina topishimiz mumkin:

\[\begin(align) & ((a)_(3))-((a)_(1))=12-2=10; \\ & ((a)_(3))-((a)_(1))=\chap(3-1 \o'ng)\cdot d=2d; \\ & 2d=10\Oʻng strelka d=5. \\ \end (tekislash)\]

Qolgan a'zolarni topishgina qoladi:

\[\begin(align) & ((a)_(1))=2; \\ & ((a)_(2))=2+5=7; \\ & ((a)_(3))=12; \\ & ((a)_(4))=2+3\cdot 5=17; \\ & ((a)_(5))=2+4\cdot 5=22; \\ & ((a)_(6))=2+5\cdot 5=27; \\ & ((a)_(7))=2+6\cdot 5=32; \\ & ((a)_(8))=2+7\cdot 5=37; \\ & ((a)_(9))=2+8\cdot 5=42; \\ \end (tekislash)\]

Shunday qilib, 9-bosqichda biz ketma-ketlikning chap tomoniga kelamiz - 42 raqami. Hammasi bo'lib, faqat 7 ta raqamni kiritish kerak edi: 7; 12; 17; 22; 27; 32; 37.

Javob: 7; 12; 17; 22; 27; 32; 37

Jarayonlar bilan matnli topshiriqlar

Xulosa qilib aytganda, men bir nechtasini ko'rib chiqmoqchiman oddiy vazifalar. Xo'sh, oddiy bo'lganlar: maktabda matematikani o'rganadigan va yuqorida yozilganlarni o'qimagan ko'pchilik o'quvchilar uchun bu vazifalar imo-ishora kabi ko'rinishi mumkin. Shunga qaramay, matematikada OGE va USEda aynan shunday vazifalar uchraydi, shuning uchun men ular bilan tanishib chiqishingizni maslahat beraman.

Vazifa raqami 11. Jamoa yanvar oyida 62 ta detal ishlab chiqargan bo‘lsa, keyingi har bir oyda oldingisiga nisbatan 14 ta ko‘p detal ishlab chiqargan. Noyabr oyida brigada nechta detal ishlab chiqardi?

Yechim. Shubhasiz, oylar bo'yicha bo'yalgan qismlar soni ortib borayotgan arifmetik progressiya bo'ladi. Va:

\[\begin(align) & ((a)_(1))=62;\quad d=14; \\ & ((a)_(n))=62+\chap(n-1 \o'ng)\cdot 14. \\ \end(hizala)\]

Noyabr - yilning 11 oyi, shuning uchun biz $((a)_(11))$ topishimiz kerak:

\[((a)_(11))=62+10\cdot 14=202\]

Shuning uchun noyabr oyida 202 ta detal ishlab chiqariladi.

Vazifa raqami 12. Kitob jilovlash ustaxonasi yanvar oyida 216 ta kitobni jamladi va har oyda oldingi oyga qaraganda 4 taga koʻp kitob muqovalandi. Dekabr oyida ustaxonada nechta kitob bog'landi?

Yechim. Hammasi bir xil:

$\begin(align) & (a)_(1))=216;\quad d=4; \\ & ((a)_(n))=216+\chap(n-1 \o'ng)\cdot 4. \\ \end(align)$

Dekabr - yilning oxirgi, 12- oyi, shuning uchun biz $((a)_(12))$ qidiramiz:

\[((a)_(12))=216+11\cdot 4=260\]

Bu javob - dekabr oyida 260 ta kitob bog'lanadi.

Xo'sh, agar siz shu paytgacha o'qigan bo'lsangiz, sizni tabriklashga shoshildim: arifmetik progressiyadagi "yosh jangchilar kursini" muvaffaqiyatli yakunladingiz. Biz keyingi darsga ishonch bilan o'tishimiz mumkin, u erda biz progressiya yig'indisi formulasini, shuningdek, undan muhim va juda foydali natijalarni o'rganamiz.

Algebrani o'rganayotganda umumta'lim maktabi(9-sinf) muhim mavzulardan biri o'rganishdir raqamlar ketma-ketligi, unga progressiyalar kiradi - geometrik va arifmetik. Ushbu maqolada biz arifmetik progressiya va yechimlari bilan misollarni ko'rib chiqamiz.

Arifmetik progressiya nima?

Buni tushunish uchun ko'rib chiqilayotgan progressiyaning ta'rifini berish, shuningdek, muammolarni hal qilishda keyinchalik qo'llaniladigan asosiy formulalarni berish kerak.

Arifmetik yoki shunday tartiblangan ratsional sonlar to'plami bo'lib, ularning har bir a'zosi oldingisidan qandaydir doimiy qiymat bilan farq qiladi. Bu qiymat farq deb ataladi. Ya'ni, tartiblangan raqamlar qatorining istalgan a'zosini va farqni bilib, butun arifmetik progressiyani tiklashingiz mumkin.

Keling, bir misol keltiraylik. Keyingi raqamlar ketma-ketligi arifmetik progressiya bo'ladi: 4, 8, 12, 16, ..., chunki bu holda farq 4 ga teng (8 - 4 = 12 - 8 = 16 - 12). Ammo 3, 5, 8, 12, 17 raqamlar to'plamini endi ko'rib chiqilayotgan progressiya turiga bog'lash mumkin emas, chunki u uchun farq doimiy qiymat emas (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠). 17 - 12).

Muhim formulalar

Endi biz arifmetik progressiya yordamida muammolarni yechish uchun zarur bo'ladigan asosiy formulalarni beramiz. a n belgisi bilan belgilang n-a'zo n butun son bo'lgan ketma-ketliklar. Farq lotincha d harfi bilan belgilanadi. Keyin quyidagi ifodalar to'g'ri bo'ladi:

1. N-sonning qiymatini aniqlash uchun formula mos keladi: a n \u003d (n-1) * d + a 1.
2. Birinchi n ta hadning yig'indisini aniqlash uchun: S n = (a n + a 1)*n/2.

9-sinfda yechim bilan arifmetik progressiyaning har qanday misollarini tushunish uchun ushbu ikkita formulani eslab qolish kifoya, chunki ko'rib chiqilayotgan turdagi har qanday muammolar ulardan foydalanish asosida qurilgan. Bundan tashqari, progressiya farqi formula bilan aniqlanishini unutmang: d = a n - a n-1 .

1-misol: Noma'lum a'zoni topish

Biz arifmetik progressiyaning oddiy misolini va yechish uchun ishlatilishi kerak bo'lgan formulalarni keltiramiz.

10, 8, 6, 4, ... ketma-ketligi berilsin, unda beshta hadni topish kerak.

Muammoning shartlaridan kelib chiqadiki, dastlabki 4 ta atama ma'lum. Beshinchisini ikki yo'l bilan aniqlash mumkin:

1. Keling, avval farqni hisoblaylik. Bizda: d = 8 - 10 = -2. Xuddi shunday, bir-birining yonida turgan ikkita boshqa atamani olish mumkin. Masalan, d = 4 - 6 = -2. Ma'lumki, d \u003d a n - a n-1, keyin d \u003d a 5 - a 4, biz qaerdan olamiz: a 5 \u003d a 4 + d. Biz ma'lum qiymatlarni almashtiramiz: a 5 = 4 + (-2) = 2.
2. Ikkinchi usul, shuningdek, ko'rib chiqilayotgan progressiyaning farqini bilishni talab qiladi, shuning uchun siz avval yuqorida ko'rsatilganidek, uni aniqlashingiz kerak (d = -2). Birinchi had a 1 = 10 ekanligini bilib, biz ketma-ketlikning n raqami uchun formuladan foydalanamiz. Bizda: a n \u003d (n - 1) * d + a 1 \u003d (n - 1) * (-2) + 10 \u003d 12 - 2 * n. Oxirgi ifodada n = 5 ni almashtirsak, biz quyidagilarni olamiz: a 5 = 12-2 * 5 = 2.

Ko'rib turganingizdek, ikkala yechim ham bir xil natijaga olib keladi. E'tibor bering, bu misolda progressiyaning d farqi manfiy. Bunday ketma-ketliklar kamayuvchi deb ataladi, chunki har bir keyingi atama oldingisidan kichikdir.

2-misol: progressiya farqi

Endi vazifani biroz murakkablashtiramiz, arifmetik progressiyaning ayirmasini topishga misol keltiramiz.

Ma'lumki, ba'zi algebraik progressiyalarda 1-hash 6 ga, 7-hash 18 ga teng bo'ladi.Ayrılmani topib, bu ketma-ketlikni 7-hashga qaytarish kerak.

Noma'lum atamani aniqlash uchun formuladan foydalanamiz: a n = (n - 1) * d + a 1 . Shartdan ma'lum ma'lumotlarni, ya'ni a 1 va 7 raqamlarini almashtiramiz, bizda: 18 \u003d 6 + 6 * d. Ushbu ifodadan siz farqni osongina hisoblashingiz mumkin: d = (18 - 6) / 6 = 2. Shunday qilib, masalaning birinchi qismiga javob berildi.

7 ta atamagacha bo'lgan ketma-ketlikni tiklash uchun ta'rifdan foydalanish kerak algebraik progressiya, ya'ni a 2 = a 1 + d, a 3 = a 2 + d va hokazo. Natijada, biz butun ketma-ketlikni tiklaymiz: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16 va 7 = 18.

3-misol: progressiya qilish

Keling, muammoning holatini yanada murakkablashtiraylik. Endi siz arifmetik progressiyani qanday topish mumkinligi haqidagi savolga javob berishingiz kerak. Quyidagi misolni keltirishimiz mumkin: ikkita son berilgan, masalan, 4 va 5. Bular orasiga yana uchta had mos kelishi uchun algebraik progressiya qilish kerak.

Ushbu muammoni hal qilishni boshlashdan oldin, berilgan raqamlar kelajakdagi rivojlanishda qaysi o'rinni egallashini tushunish kerak. Ular orasida yana uchta atama bo'ladi, keyin 1 \u003d -4 va 5 \u003d 5. Buni o'rnatgandan so'ng, biz avvalgisiga o'xshash vazifaga o'tamiz. Shunga qaramay, n-son uchun biz formuladan foydalanamiz, biz olamiz: a 5 \u003d a 1 + 4 * d. Kimdan: d \u003d (a 5 - a 1) / 4 \u003d (5 - (-4)) / 4 \u003d 2.25. Bu erda farq butun son emas, balki ratsional sondir, shuning uchun algebraik progressiya uchun formulalar bir xil bo'lib qoladi.

Endi topilgan farqni 1 ga qo'shamiz va progressiyaning etishmayotgan a'zolarini tiklaymiz. Biz olamiz: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, 5 \u003d 2,75 + 2,25 \u00, bu muammoning holatiga to'g'ri keldi.

4-misol: progressiyaning birinchi a'zosi

Yechimli arifmetik progressiyaga misollar keltirishda davom etamiz. Oldingi barcha masalalarda algebraik progressiyaning birinchi soni ma'lum edi. Endi boshqa turdagi masalani ko'rib chiqing: ikkita raqam berilsin, bu erda a 15 = 50 va 43 = 37. Bu ketma-ketlik qaysi raqamdan boshlanishini topish kerak.

Hozirgacha qo'llanilgan formulalar 1 va d ni bilishni nazarda tutadi. Muammoning holatida bu raqamlar haqida hech narsa ma'lum emas. Shunga qaramay, bizda ma'lumotga ega bo'lgan har bir atama uchun iboralarni yozamiz: a 15 = a 1 + 14 * d va 43 = a 1 + 42 * d. Biz ikkita noma'lum miqdor (a 1 va d) mavjud bo'lgan ikkita tenglama oldik. Demak, masala chiziqli tenglamalar sistemasini echishga keltiriladi.

Agar har bir tenglamada 1 ni ifodalasangiz va natijada olingan ifodalarni solishtirsangiz, belgilangan tizimni yechish eng oson hisoblanadi. Birinchi tenglama: a 1 = a 15 - 14 * d = 50 - 14 * d; ikkinchi tenglama: a 1 \u003d a 43 - 42 * d \u003d 37 - 42 * d. Ushbu iboralarni tenglashtirib, biz quyidagilarni olamiz: 50 - 14 * d \u003d 37 - 42 * d, farq d \u003d (37 - 50) / (42 - 14) \u003d - 0,464 (faqat 3 kasr berilgan).

d bilgan holda, 1 uchun yuqoridagi 2 ta ifodadan istalgan birini ishlatishingiz mumkin. Masalan, birinchi: a 1 \u003d 50 - 14 * d \u003d 50 - 14 * (- 0,464) \u003d 56,496.

Agar natijaga shubha tug'ilsa, uni tekshirishingiz mumkin, masalan, shartda ko'rsatilgan progressiyaning 43-a'zosini aniqlang. Biz olamiz: a 43 \u003d a 1 + 42 * d \u003d 56.496 + 42 * (- 0.464) \u003d 37.008. Kichik xatolik hisob-kitoblarda mingdan birgacha yaxlitlash ishlatilganligi bilan bog'liq.

5-misol: summa

Endi arifmetik progressiya yig‘indisining yechimlari bilan bir necha misollarni ko‘rib chiqamiz.

Quyidagi ko'rinishdagi sonli progressiya berilsin: 1, 2, 3, 4, ...,. Ushbu raqamlarning 100 tasining yig'indisini qanday hisoblash mumkin?

Kompyuter texnologiyalarining rivojlanishi tufayli bu muammoni hal qilish mumkin, ya'ni odam Enter tugmachasini bosgandan so'ng kompyuter bajaradigan barcha raqamlarni ketma-ket yig'ish. Biroq, agar siz taqdim etilgan raqamlar qatori algebraik progressiya ekanligiga e'tibor qaratsangiz va uning farqi 1 ga teng bo'lsa, muammoni aqliy ravishda hal qilish mumkin. / 2 = 100 * (1 + 100) / 2 = 5050.

Shunisi qiziqki, bu muammo "Gauss" deb ataladi, chunki 18-asrning boshlarida mashhur nemis hali atigi 10 yoshda bo'lganida, uni bir necha soniya ichida hal qila oldi. Bola algebraik progressiya yig'indisi formulasini bilmas edi, lekin u agar ketma-ketlikning chetida joylashgan juft raqamlarni qo'shsangiz, har doim bir xil natijaga ega bo'lishingizni payqadi, ya'ni 1 + 100 = 2 + 99. = 3 + 98 = ... va bu summalar aniq 50 (100 / 2) bo'lganligi sababli, to'g'ri javobni olish uchun 50 ni 101 ga ko'paytirish kifoya.

6-misol: n dan m gacha bo'lgan atamalar yig'indisi

Boshqa tipik misol arifmetik progressiyaning yig'indisi quyidagicha: raqamlar qatori berilgan: 3, 7, 11, 15, ..., uning 8 dan 14 gacha bo'lgan hadlari yig'indisi qanday bo'lishini topishingiz kerak.

Muammo ikki yo'l bilan hal qilinadi. Ulardan birinchisi 8 dan 14 gacha bo'lgan noma'lum atamalarni topib, keyin ularni ketma-ket umumlashtirishni o'z ichiga oladi. Bir nechta atamalar mavjud bo'lganligi sababli, bu usul etarlicha mashaqqatli emas. Shunga qaramay, bu muammoni ko'proq universal bo'lgan ikkinchi usul bilan hal qilish taklif etiladi.

Maqsad m va n hadlar orasidagi algebraik progressiya yig’indisi formulasini olishdir, bunda n > m butun sonlardir. Ikkala holatda ham yig'indi uchun ikkita ifoda yozamiz:

1. S m \u003d m * (a m + a 1) / 2.
2. S n \u003d n * (a n + a 1) / 2.

n > m bo'lgani uchun 2 yig'indiga birinchisini kiritishi aniq. Oxirgi xulosa shuni anglatadiki, agar bu yig’indilar orasidagi ayirmani olib, unga a m atamasini qo’shsak (farq olinganda S n yig’indisidan ayiriladi), u holda masalaga kerakli javobni olamiz. Bizda: S mn \u003d S n - S m + am \u003d n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am \u003d a 1 * (n - m) / 2 + an * n / 2 + am * (1-m / 2). Bu ifodada a n va a m formulalarini almashtirish kerak. Keyin biz olamiz: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1) - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Olingan formula biroz og'ir, ammo S mn yig'indisi faqat n, m, a 1 va d ga bog'liq. Bizning holatda a 1 = 3, d = 4, n = 14, m = 8. Bu raqamlarni almashtirsak, biz quyidagilarga erishamiz: S mn = 301.

Yuqoridagi yechimlardan ko‘rinib turibdiki, barcha masalalar n-sonli ifoda va birinchi hadlar to‘plami yig‘indisi formulasini bilishga asoslangan. Ushbu muammolardan birini hal qilishni boshlashdan oldin, shartni diqqat bilan o'qib chiqishingiz, nimani topmoqchi ekanligingizni aniq tushunishingiz va shundan keyingina hal qilishni davom ettirishingiz tavsiya etiladi.

Yana bir maslahat - soddalikka intiling, ya'ni agar siz murakkab matematik hisob-kitoblardan foydalanmasdan savolga javob bera olsangiz, unda siz buni qilishingiz kerak, chunki bu holda xato qilish ehtimoli kamroq. Masalan, 6-sonli yechim bilan arifmetik progressiya misolida, S mn \u003d n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am formulasida to'xtash mumkin, va umumiy topshiriqni alohida kichik vazifalarga ajrating (bu holda, birinchi navbatda a va am atamalarini toping).

Olingan natijaga shubha tug'ilsa, berilgan misollarning ba'zilarida bo'lgani kabi, uni tekshirish tavsiya etiladi. Arifmetik progressiyani qanday topish mumkinligi aniqlandi. Buni tushunganingizdan so'ng, bu unchalik qiyin emas.

Ko'rsatma

Arifmetik progressiya a1, a1+d, a1+2d..., a1+(n-1)d ko‘rinishdagi ketma-ketlikdir. d raqami qadam progressiyalar.Shubhasiz, arifmetikaning ixtiyoriy n-chi hadi yig’indisi progressiyalar shaklga ega: An = A1+(n-1)d. Keyin a'zolardan birini bilish progressiyalar, a'zo progressiyalar va qadam progressiyalar, bo'lishi mumkin, ya'ni progressiya hadining soni. Shubhasiz, u n = (An-A1+d)/d formulasi bilan aniqlanadi.

Endi mth atamasi ma'lum bo'lsin progressiyalar va boshqa a'zolar progressiyalar- n-th, lekin n , oldingi holatda bo'lgani kabi, lekin ma'lumki, n va m mos kelmaydi.Step progressiyalar formula bilan hisoblash mumkin: d = (An-Am)/(n-m). Keyin n = (An-Am+md)/d.

Agar arifmetikaning bir nechta elementlari yig'indisi bo'lsa progressiyalar, shuningdek, uning birinchi va oxirgi , keyin bu elementlarning sonini ham aniqlash mumkin.Arifmetik yig'indisi progressiyalar teng bo'ladi: S = ((A1+An)/2)n. U holda n = 2S/(A1+An) chdenovdir progressiyalar. An = A1+(n-1)d ekanligidan foydalanib, bu formulani quyidagicha qayta yozish mumkin: n = 2S/(2A1+(n-1)d). Bundan kvadrat tenglamani yechish orqali n ni ifodalash mumkin.

Arifmetik ketma-ketlik shunday tartiblangan raqamlar to'plami bo'lib, ularning har bir a'zosi, birinchisidan tashqari, oldingisidan bir xil miqdorda farq qiladi. Bu doimiy progressiya yoki uning qadamining ayirmasi deb ataladi va arifmetik progressiyaning ma'lum a'zolaridan hisoblanishi mumkin.

Ko'rsatma

Agar birinchi va ikkinchi yoki boshqa qo'shni shartlarning qiymatlari masala shartlaridan ma'lum bo'lsa, farqni (d) hisoblash uchun keyingi haddan oldingi hadni ayirish kifoya. Olingan qiymat ijobiy yoki salbiy bo'lishi mumkin - bu progressiyaning ortib borayotganiga bog'liq. Umumiy shaklda progressiyaning qo'shni a'zolarining ixtiyoriy juftligi (aᵢ va aᵢ₊₁) uchun yechimni quyidagicha yozing: d = aᵢ₊₁ - aᵢ.

Bunday progressiyaning bittasi birinchi (a₁), ikkinchisi esa ixtiyoriy tanlangan boshqa juft a'zolar uchun ayirma (d) ni topish formulasini ham tuzish mumkin. Biroq, bu holda, ketma-ketlikning o'zboshimchalik bilan tanlangan a'zosining seriya raqami (i) ma'lum bo'lishi kerak. Farqni hisoblash uchun ikkala raqamni qo'shing va natijani bittaga qisqartirilgan ixtiyoriy atamaning tartib raqamiga bo'ling. V umumiy ko'rinish bu formulani shunday yozing: d = (a₁+ aᵢ)/(i-1).

Agar tartib raqami i bo‘lgan arifmetik progressiyaning ixtiyoriy a’zosidan tashqari, tartib raqami u bo‘lgan boshqa a’zosi ma’lum bo‘lsa, avvalgi bosqichdagi formulani shunga mos ravishda o‘zgartiring. Bunday holda, progressiyaning farqi (d) bu ikki hadning yig'indisi ularning tartib raqamlari farqiga bo'linadi: d = (aᵢ+aᵥ)/(i-v).

Farqni (d) hisoblash formulasi, agar masala sharoitida uning birinchi a'zosining qiymati (a₁) va berilgan sonning (i) birinchi a'zolarining yig'indisi (Sᵢ) bo'lsa, biroz murakkablashadi. arifmetik ketma-ketlik berilgan. Kerakli qiymatni olish uchun yig'indini uni tashkil etgan shartlar soniga bo'ling, ketma-ketlikdagi birinchi raqamning qiymatini ayirib, natijani ikki baravar oshiring. Olingan qiymatni bittaga kamaytirilgan yig'indini tashkil etgan shartlar soniga bo'ling. Umuman olganda, diskriminantni hisoblash formulasini quyidagicha yozing: d = 2*(Sᵢ/i-a₁)/(i-1).

Diqqat!
Qo'shimchalar mavjud
555-sonli maxsus bo'limdagi materiallar.
Qattiq "juda emas..." deganlar uchun.
Va "juda ..." bo'lganlar uchun)

Arifmetik progressiya - bu har bir raqam oldingisidan bir xil miqdorda katta (yoki kamroq) bo'lgan raqamlar qatoridir.

Bu mavzu ko'pincha qiyin va tushunarsiz. Harf ko'rsatkichlari, progressiyaning n-a'zosi, progressiyaning farqi - bularning barchasi qandaydir chalkash, ha ... Keling, arifmetik progressiyaning ma'nosini aniqlaylik va hamma narsa darhol amalga oshadi.)

Arifmetik progressiya haqida tushuncha.

Arifmetik progressiya juda oddiy va tushunarli tushunchadir. Shubha? Bekorga.) O'zingiz ko'ring.

Men tugallanmagan raqamlar qatorini yozaman:

1, 2, 3, 4, 5, ...

Bu qatorni uzaytira olasizmi? Qaysi raqamlar beshdan keyin keladi? Har bir inson ... uh ..., qisqasi, har bir kishi 6, 7, 8, 9 va hokazo raqamlarning oldinga borishini aniqlaydi.

Keling, vazifani murakkablashtiraylik. Men tugallanmagan raqamlar qatorini beraman:

2, 5, 8, 11, 14, ...

Siz naqshni ushlashingiz, seriyani kengaytirishingiz va nomlashingiz mumkin yettinchi qator raqami?

Agar siz bu raqam 20 ekanligini bilsangiz - sizni tabriklayman! Siz nafaqat his qildingiz arifmetik progressiyaning asosiy nuqtalari; balki ularni biznesda ham muvaffaqiyatli ishlatgan! Agar tushunmasangiz, o'qing.

Endi sezgilardan asosiy fikrlarni matematikaga aylantiramiz.)

Birinchi asosiy nuqta.

Arifmetik progressiya sonlar qatori bilan bog'liq. Bu birinchi navbatda chalkash. Biz tenglamalarni echishga, grafiklar tuzishga va shunga o'rganib qolganmiz ... Va keyin qatorni kengaytiring, qatorlar sonini toping ...

Hech narsa xato emas. Shunchaki progressiyalar matematikaning yangi bo‘limi bilan birinchi tanishuvdir. Bo'lim "Seriya" deb nomlanadi va raqamlar va ifodalar qatori bilan ishlaydi. Bunga ko'nik.)

Ikkinchi asosiy nuqta.

Arifmetik progressiyada har qanday son oldingisidan farq qiladi bir xil miqdorda.

Birinchi misolda bu farq bitta. Qaysi raqamni olsangiz, oldingisidan bittaga ko'p. Ikkinchisida - uchta. Har qanday raqam oldingisidan uch baravar katta. Aslida, aynan shu daqiqa bizga naqshni ushlash va keyingi raqamlarni hisoblash imkoniyatini beradi.

Uchinchi asosiy nuqta.

Bu daqiqa hayratlanarli emas, ha ... Lekin juda, juda muhim. Mana: har biri progressiya soni o‘z o‘rnida turadi. Birinchi raqam bor, yettinchi bor, qirq beshinchi bor va hokazo. Agar siz ularni tasodifan aralashtirib yuborsangiz, naqsh yo'qoladi. Arifmetik progressiya ham yo'qoladi. Bu shunchaki raqamlar qatori.

Hamma gap shunda.

Albatta, ichida yangi mavzu yangi atamalar va belgilar paydo bo'ladi. Ular bilishlari kerak. Aks holda, siz vazifani tushunolmaysiz. Masalan, siz shunday qaror qabul qilishingiz kerak:

a 2 = 5, d = -2,5 bo'lsa, arifmetik progressiyaning (a n) birinchi oltita hadini yozing.

Bu ilhomlantiradimi?) Harflar, ba'zi indekslar ... Va vazifa, aytmoqchi, osonroq bo'lishi mumkin emas. Siz faqat atamalar va belgilarning ma'nosini tushunishingiz kerak. Endi biz bu masalani o'zlashtiramiz va vazifaga qaytamiz.

Shartlar va belgilar.

Arifmetik progressiya har bir raqam oldingisidan farq qiladigan raqamlar qatoridir bir xil miqdorda.

Bu qiymat deyiladi . Keling, ushbu kontseptsiyani batafsil ko'rib chiqaylik.

Arifmetik progressiya farqi.

Arifmetik progressiya farqi har qanday progressiya sonining miqdori Ko'proq oldingi.

Bir muhim nuqta. Iltimos, so'zga e'tibor bering "Ko'proq". Matematik jihatdan bu har bir progressiya soni olinganligini bildiradi qo'shish arifmetik progressiyaning oldingi songa ayirmasi.

Hisoblash uchun, aytaylik ikkinchi qator raqamlari, buni qilish kerak birinchi raqam qo'shish arifmetik progressiyaning aynan shu farqi. Hisoblash uchun beshinchi- farq kerak qo'shish Kimga to'rtinchi yaxshi va boshqalar.

Arifmetik progressiya farqi balkim ijobiy keyin seriyaning har bir raqami haqiqiy bo'lib chiqadi oldingisidan ko'proq. Bu progressiya deyiladi ortib boradi. Masalan:

8; 13; 18; 23; 28; .....

Bu erda har bir raqam qo'shish ijobiy raqam, oldingisiga +5.

Farqi bo'lishi mumkin salbiy keyin seriyadagi har bir raqam bo'ladi oldingisidan kamroq. Ushbu rivojlanish deyiladi (siz bunga ishonmaysiz!) kamaymoqda.

Masalan:

8; 3; -2; -7; -12; .....

Bu erda har bir raqam ham olinadi qo'shish oldingi, lekin allaqachon salbiy raqamga -5.

Aytgancha, progressiya bilan ishlashda uning tabiatini darhol aniqlash juda foydali - u ortib bormoqda yoki kamaymoqda. Bu qaror qabul qilishda o'z nuqtai nazaringizni topishga, xatolaringizni aniqlashga va kech bo'lmasdan ularni tuzatishga yordam beradi.

Arifmetik progressiya farqi odatda harf bilan belgilanadi d.

Qanday topish mumkin d? Juda oddiy. Seriyaning istalgan sonidan ayirish kerak oldingi raqam. Ayirmoq. Aytgancha, ayirish natijasi "farq" deb ataladi.)

Keling, masalan, aniqlaymiz d ortib borayotgan arifmetik progressiya uchun:

2, 5, 8, 11, 14, ...

Biz qatorning istalgan raqamini olamiz, masalan, 11. Undan ayirish oldingi raqam bular. sakkiz:

Bu to'g'ri javob. Bu arifmetik progressiya uchun farq uchga teng.

Siz shunchaki olishingiz mumkin har qanday miqdordagi progressiya, chunki Muayyan rivojlanish uchun d-har doim bir xil. Hech bo'lmaganda qatorning boshida, hech bo'lmaganda o'rtada, hech bo'lmaganda har qanday joyda. Siz faqat birinchi raqamni ololmaysiz. Faqat birinchi raqam, chunki oldingisi yo'q.)

Aytgancha, buni bilish d=3, bu progressiyaning ettinchi raqamini topish juda oddiy. Biz beshinchi raqamga 3 qo'shamiz - biz oltinchini olamiz, u 17 bo'ladi. Oltinchi raqamga uchta qo'shamiz, ettinchi raqamni olamiz - yigirma.

Keling, aniqlaymiz d kamayuvchi arifmetik progressiya uchun:

8; 3; -2; -7; -12; .....

Shuni eslatib o'tamanki, belgilardan qat'i nazar, aniqlash uchun d istalgan raqamdan kerak oldingisini olib tashlang. Biz progressiyaning istalgan sonini tanlaymiz, masalan -7. Uning oldingi raqami -2. Keyin:

d = -7 - (-2) = -7 + 2 = -5

Arifmetik progressiyaning farqi har qanday son bo'lishi mumkin: butun, kasr, irratsional, har qanday.

Boshqa atamalar va belgilar.

Seriyadagi har bir raqam chaqiriladi arifmetik progressiyaning a'zosi.

Progressiyaning har bir a'zosi uning raqami bor. Raqamlar qat'iy tartibda, hech qanday hiyla-nayranglarsiz. Birinchi, ikkinchi, uchinchi, to'rtinchi va boshqalar. Masalan, progressiyadagi 2, 5, 8, 11, 14, ... ikkita birinchi a'zo, beshta ikkinchi, o'n bir to'rtinchi, yaxshi, tushunasiz ...) Iltimos, aniq tushuning - raqamlarning o'zi mutlaqo har qanday, butun, kasr, inkor, nima bo'lishidan qat'iy nazar, lekin bo'lishi mumkin raqamlash- qat'iy tartibda!

Progressiyani umumiy shaklda qanday yozish kerak? Hammasi joyida! Seriyadagi har bir raqam harf sifatida yozilgan. Arifmetik progressiyani belgilash uchun, qoida tariqasida, harf ishlatiladi a. A'zo raqami pastki o'ngdagi indeks bilan ko'rsatilgan. A'zolar vergul (yoki nuqta vergul) bilan quyidagicha yoziladi:

a 1 , a 2 , a 3 , a 4 , a 5 , .....

a 1 birinchi raqam hisoblanadi a 3- uchinchi va boshqalar. Hech qanday qiyin narsa yo'q. Siz ushbu seriyani quyidagicha qisqacha yozishingiz mumkin: (a n).

Rivojlanishlar mavjud chekli va cheksiz.

yakuniy progressiya a'zolarining cheklangan soniga ega. Besh, o'ttiz sakkiz, nima bo'lishidan qat'iy nazar. Lekin bu chekli raqam.

Cheksiz progressiya - siz taxmin qilganingizdek, cheksiz sonli a'zolarga ega.)

Siz yakuniy progressni shunday qator orqali yozishingiz mumkin, barcha a'zolar va oxirida nuqta:

a 1, 2, 3, 4, 5.

Yoki shunga o'xshash, agar a'zolar ko'p bo'lsa:

a 1, a 2, ... a 14, a 15.

Qisqa yozuvda siz a'zolar sonini qo'shimcha ravishda ko'rsatishingiz kerak bo'ladi. Misol uchun (yigirma a'zo uchun) quyidagicha:

(a n), n = 20

Cheksiz progressiyani ushbu darsdagi misollardagi kabi qator oxiridagi ellips bilan tanib olish mumkin.

Endi siz allaqachon vazifalarni hal qilishingiz mumkin. Vazifalar oddiy, faqat arifmetik progressiyaning ma'nosini tushunish uchun.

Arifmetik progressiya uchun topshiriqlarga misollar.

Keling, yuqoridagi vazifani batafsil ko'rib chiqaylik:

1. Arifmetik progressiyaning (a n) birinchi olti a'zosini yozing, agar a 2 = 5, d = -2,5.

Vazifani tushunarli tilga tarjima qilamiz. Cheksiz arifmetik progressiya berilgan. Ushbu progressiyaning ikkinchi soni ma'lum: a 2 = 5. Ma'lum progressiv farq: d = -2,5. Ushbu progressiyaning birinchi, uchinchi, to'rtinchi, beshinchi va oltinchi a'zolarini topishimiz kerak.

Aniqlik uchun men muammoning holatiga qarab ketma-ket yozaman. Birinchi olti a'zo, ikkinchi a'zo besh bo'lsa:

a 1, 5, 3, 4, 5, 6,....

a 3 = a 2 + d

Biz ifodada almashtiramiz a 2 = 5 va d=-2,5. Minusni unutmang!

a 3=5+(-2,5)=5 - 2,5 = 2,5

Uchinchi muddat ikkinchidan kamroq. Hammasi mantiqiy. Agar raqam avvalgisidan katta bo'lsa salbiy qiymat, shuning uchun raqamning o'zi avvalgisidan kamroq bo'ladi. Rivojlanish pasaymoqda. Xo'sh, buni hisobga olamiz.) Biz seriyamizning to'rtinchi a'zosini ko'rib chiqamiz:

a 4 = a 3 + d

a 4=2,5+(-2,5)=2,5 - 2,5 = 0

a 5 = a 4 + d

a 5=0+(-2,5)= - 2,5

a 6 = a 5 + d

a 6=-2,5+(-2,5)=-2,5 - 2,5 = -5

Shunday qilib, uchinchidan oltinchigacha bo'lgan muddatlar hisoblab chiqilgan. Natijada bir qator paydo bo'ldi:

a 1, 5, 2,5, 0, -2,5, -5, ....

Birinchi atamani topish qoladi a 1 yoqilgan mashhur ikkinchi. Bu boshqa yo'nalishdagi qadam, chapga.) Demak, arifmetik progressiyaning farqi d ga qo'shilmasligi kerak a 2, a olib ketish:

a 1 = a 2 - d

a 1=5-(-2,5)=5 + 2,5=7,5

Hammasi shu. Vazifaga javob:

7,5, 5, 2,5, 0, -2,5, -5, ...

O'tayotganda shuni ta'kidlaymanki, biz bu vazifani hal qildik takrorlanuvchi yo'l. Bu dahshatli so'z faqat progressiyaning a'zosini qidirishni anglatadi oldingi (qo'shni) raqam bo'yicha. Progressiya bilan ishlashning boshqa usullari keyinroq muhokama qilinadi.

Ushbu oddiy vazifadan bitta muhim xulosa chiqarish mumkin.

Eslab qoling:

Agar arifmetik progressiyaning kamida bitta a’zosi va ayirmasini bilsak, bu progressiyaning istalgan a’zosini topishimiz mumkin.

Esingizdami? Ushbu oddiy hosila bizga ko'p muammolarni hal qilish imkonini beradi maktab kursi ushbu mavzu bo'yicha. Barcha vazifalar uchta asosiy parametr atrofida aylanadi: arifmetik progressiya a’zosi, progressiyaning ayirmasi, progressiya a’zosining soni. Hamma narsa.

Albatta, oldingi barcha algebra bekor qilinmaydi.) Progressiyaga tengsizliklar, tenglamalar va boshqa narsalar biriktiriladi. Lekin taraqqiyotiga ko'ra- hamma narsa uchta parametr atrofida aylanadi.

Misol uchun, ushbu mavzu bo'yicha ba'zi mashhur vazifalarni ko'rib chiqing.

2. Yakuniy arifmetik progressiyani ketma-ket yozing, agar n=5, d=0,4 va a 1=3,6 bo‘lsa.

Bu erda hamma narsa oddiy. Hammasi allaqachon berilgan. Arifmetik progressiyaning a'zolari qanday hisoblanganini, hisoblashini va yozishni eslab qolishingiz kerak. Vazifa shartidagi so'zlarni o'tkazib yubormaslik tavsiya etiladi: "yakuniy" va " n=5". To'liq ko'karib qolmaguningizcha hisoblamaslik uchun.) Bu progressiyada faqat 5 (besh) a'zo bor:

a 2 \u003d a 1 + d \u003d 3,6 + 0,4 \u003d 4

a 3 \u003d a 2 + d \u003d 4 + 0,4 \u003d 4,4

a 4 = a 3 + d = 4,4 + 0,4 = 4,8

a 5 = a 4 + d = 4,8 + 0,4 = 5,2

Javobni yozish qoladi:

3,6; 4; 4,4; 4,8; 5,2.

Boshqa vazifa:

3. 7 soni arifmetik progressiyaning (a n) a’zosi bo‘ladimi yoki yo‘qligini aniqlang, agar a 1 \u003d 4.1; d = 1,2.

Hm... Kim biladi? Biror narsani qanday aniqlash mumkin?

How-how... Ha, progressiyani ketma-ketlik shaklida yozing va ettita bo'ladimi yoki yo'qmi! Ishonamizki:

a 2 \u003d a 1 + d \u003d 4,1 + 1,2 \u003d 5,3

a 3 \u003d a 2 + d \u003d 5,3 + 1,2 \u003d 6,5

a 4 = a 3 + d = 6,5 + 1,2 = 7,7

4,1; 5,3; 6,5; 7,7; ...

Endi biz yetti yoshda ekanligimiz aniq ko'rinib turibdi sirg'alib o'tdi 6,5 dan 7,7 gacha! Yettilik bizning raqamlar qatorimizga kirmadi va shuning uchun ettitasi berilgan progressiyaning a'zosi bo'lmaydi.

Javob: yo'q.

Va bu erda bir muammo asoslangan haqiqiy versiya GIA:

4. Arifmetik progressiyaning bir necha ketma-ket a'zolari yoziladi:

...; 15; X; 9; 6; ...

Mana oxiri va boshi bo'lmagan seriya. A'zolar raqamlari yo'q, farq yo'q d. Hech narsa xato emas. Muammoni hal qilish uchun arifmetik progressiyaning ma'nosini tushunish kifoya. Keling, nima qila olishimizni ko'rib chiqaylik kashf qilish bu qatordan? Uchta asosiy parametrlar qanday?

A'zolar raqamlari? Bu erda bitta raqam yo'q.

Ammo uchta raqam bor va - diqqat! - so'z "ketma-ket" holatda. Bu raqamlar qat'iy tartibda, bo'shliqlarsiz ekanligini anglatadi. Bu qatorda ikkitasi bormi? qo'shni ma'lum raqamlar? Ha bor! Bular 9 va 6. Shunday qilib, biz arifmetik progressiyaning farqini hisoblay olamiz! Biz oltitadan ayiramiz oldingi raqam, ya'ni. to'qqiz:

Bo'sh joylar qoldi. X uchun oldingi qaysi raqam bo'ladi? O'n besh. Shunday qilib, x ni oddiy qo'shish orqali osongina topish mumkin. 15 ga arifmetik progressiyaning farqini qo'shing:

Ana xolos. Javob: x=12

Quyidagi muammolarni o'zimiz hal qilamiz. Eslatma: bu boshqotirmalar formulalar uchun emas. Faqat arifmetik progressiyaning ma'nosini tushunish uchun.) Biz shunchaki bir qator raqamlar-harflarni yozamiz, qaraymiz va o'ylaymiz.

5. a 5 = -3 bo'lsa, arifmetik progressiyaning birinchi musbat hadini toping; d = 1,1.

6. Ma'lumki, 5,5 soni arifmetik progressiyaning (a n) a'zosi bo'lib, bu erda a 1 = 1,6; d = 1,3. Bu atamaning n sonini aniqlang.

7. Ma'lumki, arifmetik progressiyada a 2 = 4; a 5 \u003d 15.1. 3 ni toping.

8. Arifmetik progressiyaning bir necha ketma-ket a'zolari yoziladi:

...; 15,6; X; 3.4; ...

X harfi bilan belgilangan progressiyaning hadini toping.

9. Poyezd stansiyadan harakatlana boshladi, asta-sekin tezligini daqiqasiga 30 metrga oshirdi. Besh daqiqada poezdning tezligi qanday bo'ladi? Javobingizni km/soatda bering.

10. Ma'lumki, arifmetik progressiyada a 2 = 5; a 6 = -5. 1 ni toping.

Javoblar (tartibsiz): 7,7; 7,5; 9,5; 9; 0,3; 4.

Hammasi chiqdimi? Ajoyib! Ko'proq ma'lumot uchun arifmetik progressiyani o'zlashtirishingiz mumkin yuqori daraja, keyingi darslarda.

Hammasi amalga oshmadimi? Hammasi joyida. 555-sonli maxsus bo'limda bu muammolarning barchasi bo'laklarga bo'linadi.) Va, albatta, bunday vazifalarni hal qilishni darhol kaftingizda bo'lgani kabi aniq, aniq ta'kidlaydigan oddiy amaliy texnika tasvirlangan!

Aytgancha, poezd haqidagi jumboqda odamlar tez-tez qoqilib ketadigan ikkita muammo bor. Biri - faqat progressiya bilan, ikkinchisi - matematika va fizikadagi har qanday vazifalar uchun umumiydir. Bu o'lchamlarning biridan ikkinchisiga tarjimasi. Bu muammolarni qanday hal qilish kerakligini ko'rsatadi.

Ushbu darsda biz arifmetik progressiyaning elementar ma'nosini va uning asosiy parametrlarini ko'rib chiqdik. Bu mavzu bo'yicha deyarli barcha muammolarni hal qilish uchun etarli. Qo'shish d raqamlarga, ketma-ket yozing, hamma narsa hal qilinadi.

Barmoq eritmasi ushbu darsdagi misollarda bo'lgani kabi, seriyaning juda qisqa qismlari uchun yaxshi ishlaydi. Agar seriya uzunroq bo'lsa, hisob-kitoblar qiyinlashadi. Misol uchun, agar savolda 9-muammoda bo'lsa, o'zgartiring "besh daqiqa" ustida "o'ttiz besh daqiqa" muammo yanada yomonlashadi.)

Bundan tashqari, mohiyatiga ko'ra oddiy, ammo hisob-kitoblar nuqtai nazaridan mutlaqo absurd bo'lgan vazifalar mavjud, masalan:

Arifmetik progressiya (a n) berilgan. a 1 =3 va d=1/6 bo'lsa, 121 ni toping.

Va nima, biz 1/6 ni ko'p marta qo'shamiz?! O'z joniga qasd qilish mumkinmi!?

Mumkin.) Agar siz bunday vazifalarni bir daqiqada hal qilishingiz mumkin bo'lgan oddiy formulani bilmasangiz. Ushbu formula keyingi darsda bo'ladi. Va bu muammo o'sha erda hal qilinadi. Bir daqiqada.)

Agar sizga bu sayt yoqsa...

Aytgancha, menda siz uchun yana bir nechta qiziqarli saytlar bor.)

Siz misollar yechishda mashq qilishingiz va o'z darajangizni bilib olishingiz mumkin. Tezkor tekshirish bilan test. O'rganish - qiziqish bilan!)

funksiyalar va hosilalar bilan tanishishingiz mumkin.